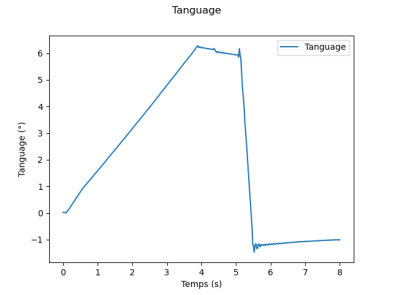
Tracés des différentes grandeurs
On va utiliser les données précédentes, on commencera par les tracés.
Question
Tracer l'angle de tangage provenant de la mesure en fonction du temps. Conclure sur la valeur de \(\ddot{\alpha}\) pendant la majorité du temps et faire une hypothèse qui permet de relier très simplement la mesure de l'accélération suivant le vecteur \(\vec{y_1}\) avec l'angle \(\alpha\).
Solution
#Q1f, ax = plt.subplots()
f.suptitle("Tanguage")
ax.set_xlabel("Temps (s)") # On légende les abscisses de la zone de tracé
ax.set_ylabel("Tanguage (°)") # On légende les ordonnées de la zone de tracé
ax.plot(temps, tangage, label="Tanguage mesuré") # On trace la courbe voulue
ax.legend() # On affiche la légende de la zone de tracé
plt.show()
On rappelle que \(\vec{a}_T = -\left(h\ddot{\alpha}+g sin\alpha\right) \vec y_1 -\left( h\dot{\alpha}^2 + g cos \alpha\right) \vec z_1\)
On approxime d'après la question précédente que \( \ddot{\alpha}\) est nulle.
Question
Déterminer alors l'angle de tangage à partir de la mesure de l'accéléromètre sur \(\vec{y_1}\) ( \(\texttt{accy}\)) et comparer à celle donnée directement par la centrale inertielle. Conclure.
Indice
\(\texttt{accy}= -\left(g sin\alpha\right) \)
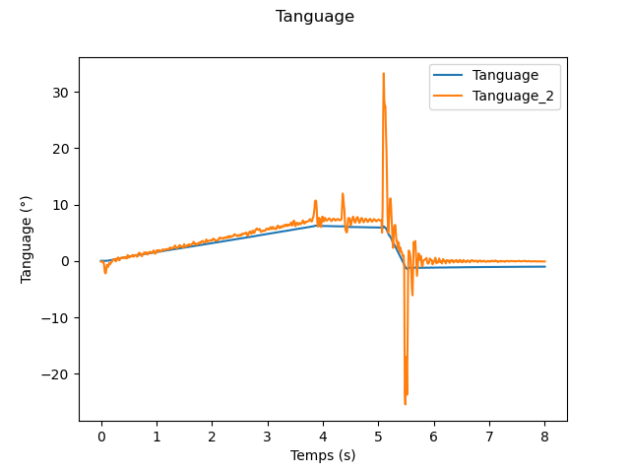
Solution
ax.plot(temps, np.arcsin(-accy/9.86)*180/np.pi, label="Tanguage_2")