Intégration
On a également la mesure de \(\dot{\alpha}\). Par intégration sur le temps, on peut obtenir \(\alpha\) : \(\alpha = \int_0^t \dot{\alpha}\, d t\)
Question
Définir une fonction \(\texttt{integration_rectangle(t,f)}\) qui prend en arguments un vecteur \(\texttt{t}\) représentant l'abscisse et un vecteur \(\texttt{f}\) représentant l'ordonnée. Cette fonction renverra une liste ou vecteur de la taille de \(\texttt{t}\) (ou \(\texttt{f}\)), l'indice \(i\) correspondra à l'intégrale de 0 à \(\texttt{t[i]}\) de la liste \(\texttt{f}\).
On pourra utiliser l'intégration par
rectangle à droite,
rectangle gauche,
point milieu
Tester votre fonction sur la variable \( \texttt{test1}=3*np.ones(len(temps)) \) qui correspond à une liste ne contenant que des 3, c'est la fonction constante 3. Le résultat est donc connu et doit donner 24 à la fin, le temps variant de 0 à 8 s.
Solution
def integration_rectangle(t,f):
sol = [0]
for i in range(1,len(f)):
sol.append(sol[i-1]+ f[i]*(t[i]-t[i-1]))
return array(sol)
test1 = 3*np.ones(len(temps)) # fonction constante y = 3
resu1 = (integration_rectangle(temps, test1))
print(resu1)
La dernière valeur est bien 24.
Question
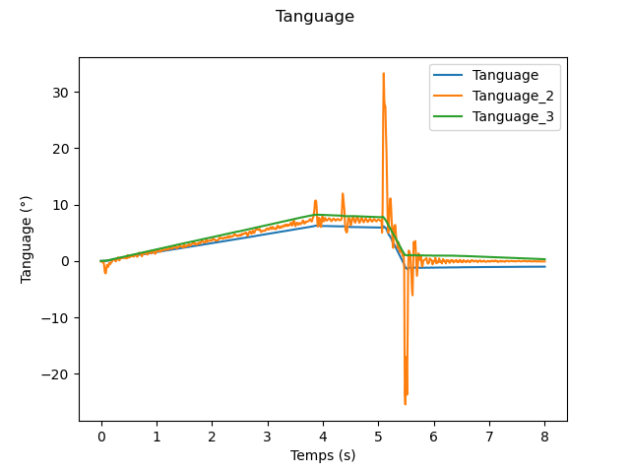
Utiliser votre fonction d’intégration sur les données de la vitesse de tangage \( \texttt{vtanguage}\) afin de calculer l'angle de tangage. Superposer l'angle de tangage mesuré à ceux calculés à partir de l'accélération sur \(\vec{y_1}\) et à partir de la vitesse de tangage. Conclure.