Calcul de l'énergie consommée

Le système est composé de deux vérins électriques. On a à notre disposition la force dans chaque vérin et la position de chaque vérin. La puissance développée par un vérin est égale au produit de la force par la vitesse \(P(t) = F(t)\times V(t)\).

Il faut donc calculer la vitesse de translation des vérins à partir des positions.

Question

Définir une fonction \(\texttt{derive(t,f)}\) qui prend en arguments une vecteur \(\texttt{t}\) représentant l'abscisse et un vecteur \(\texttt{f}\) représentant l'ordonnée. Cette fonction renvoie une liste contenant la dérivée numérique à droite, à gauche ou centrée selon votre choix. Vous veillerez à ce que la liste retournée soit de la même taille que le temps \(\texttt{t}\).

Tester votre fonction sur la variable \(\texttt{test2}\) qui représente la fonction \(3t\). La dérivée est ainsi connue et doit être égale à 3.

Solution

1
# derivation numérique à droite
2
def derivee(temps, data):
3
    vit = []
4
    for i in range(1, len(data)):
5
        vit.append((data[i]-data[i-1])/(temps[i]-temps[i-1]))
6
    vit.append(vit[-1]) #la dernière vitesse est égale à la précédente
7
    return vit
8
9
# derivation numérique centrée pour ceux qui veulent tester.
10
def derivee_centree(temps,data):
11
    vit = [(data[1]-data[0])/(temps[1]-temps[0])]
12
    for i in range(1, len(data)-1):
13
        vit.append((data[i+1]-data[i-1])/(temps[i+1]-temps[i-1]))
14
    vit.append(vit[-1]) #la dernière vitesse est égale à la précédente
15
    return vit
Question
Utiliser votre fonction pour calculer la puissance totale \(P = F_1.V_1+F_2.V_2\).
Solution
1
#Q8
2
vit1 = array(derivee(temps,pos1))
3
vit2 = array(derivee(temps,pos2))
4
puissance = force1*vit1+force2*vit2
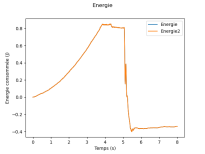
L'énergie consommée au cours du temps est l'intégrale sur le temps de la puissance.
Question
Tracer l'évolution de l'énergie consommée au cours du temps.
Solution
1
energ1 = integration_rectangle(temps, puissance)
2
figure(3)
3
plot(temps, energ1)
Question
Changer de méthode d'intégration : définir une fonction \(\texttt{integration_trapeze(t,f)}\) qui calcule l'intégrale à l'aide de la méthode des trapèzes. Tester votre fonction avec la variable \(\texttt{test2}\) dont la valeur de l'intégrale sur le temps complet est de 96. Appliquer la méthode d'intégration au calcul de l'énergie. Conclure.
Solution
1
def integration_trapeze(t, f):
2
    s=[0]
3
    for i in range(1,len(t)):
4
        s.append(s[-1]+(f[i]+f[i-1])*(t[i]-t[i-1])/2.)
5
    return array(s)