CAPACITÉS NUMÉRIQUES

L'objectif de ce TP est d'analyser des données issues de mesures sur le simulateur de course disponible dans le laboratoire de SI.

Pour cela, il faudra être capable de réaliser notamment des intégrations numériques et des dérivations numériques.

Un simulateur est un dispositif dont la fonction principale est de reproduire le plus fidèlement possible le comportement d'un système de référence (réel).

Par rapport à la conduite sur route, les simulateurs de conduite offrent trois avantages majeurs :

• ils présentent un environnement sans danger pour le conducteur (ex. accidents virtuels) ;

• une même expérience peut être répétée aussi souvent que nécessaire dans des conditions identiques ;

• ils permettent une économie considérable.

Ainsi, les simulateurs de conduite sont utilisés dans de nombreux domaines :

• travaux de recherche sur le comportement humain ;

• étude et amélioration de la sécurité ;

• aide à la conception de véhicule ou de l'environnement routier ;

• apprentissage à moindre coût ;

• loisir...

Le simulateur étudié dans ce sujet est un simulateur de course automobile à deux degrés de liberté utilisé par des particuliers dans le domaine du loisir

La structure articulée possède deux degrés de liberté (roulis et tangage) comme indiqué sur la figure suivante. Il y une liaison sphérique à doigt au point 0 pour permettre ces deux rotations.

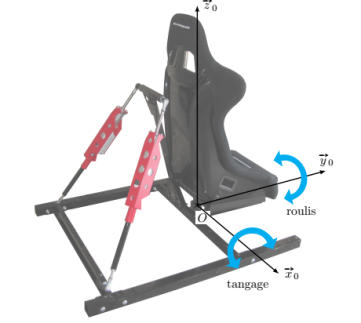
On va s'intéresser ici au cycle de prise d'origine à partir d'une position symétrique. Le mouvement est ainsi un mouvement de tangage pur. Les vérins rentrent complètement jusqu'à la butée inférieure, puis ressortent rapidement pour atteindre la position d'origine.

On note \(R_0(O, \vec x_0, \vec y_0, \vec z_0)\) le repère associé au sol (0), supposé galiléen. Le paramétrage est défini sur la figure paramétrage_tangage. L'ensemble \{conducteur + siège\} est noté (1) et est en rotation par rapport au sol (0) autour d'un axe \((O, \vec x_0)\). On associe le repère \(R_1(O, \vec x_1, \vec y_1, \vec z_1)\) à l'ensemble (1) et on note \(\alpha=(\vec y_0, \vec y_1)=(\vec z_0, \vec z_1)\) l'angle de tangage de (1) par rapport à (0).

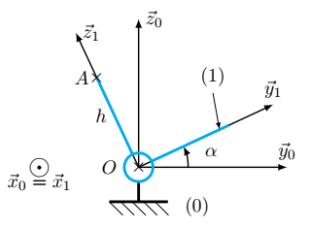
Un point de la tête proche de l'oreille interne du pilote noté \( A\) est défini par : \(\overrightarrow{OA} = h\, \vec z_1\) avec \(h=1~m\) L'accélération de la pesanteur est \(\vec{g}=-g\, \vec{z}_0\) avec \(g=9.8~m.s^{-2}\).

Le siège est piloté de telle manière que l'accélération donnée par le jeu vidéo soit équivalente à l'accélération ressentie par le pilote sur le siège. En notant \(\vec{a}_T\) l'accélération du véhicule, on obtient la définition suivante :

\(\overrightarrow{a_T} = a_{Tx}\, \vec{x}_1 + a_{Tz}\, \vec{z}_1 = \overrightarrow{{a}_{(A, 1/0)}} - \vec{g}\)

Après calcul, on a :

\(\vec{a}_T = -\left(h\ddot{\alpha}+g sin\alpha\right) \vec y_1 -\left( h\dot{\alpha}^2 + g cos \alpha\right) \vec z_1\)

Pour mesurer l'angle de tangage, une centrale inertielle est fixée sur la barre \((OA)\). Elle permet d'avoir les accélérations suivant les 3 vecteurs de la base \(R_1\), les vitesses de rotation de roulis et de tangage, les angles de roulis et de tangage directement.

L'objectif de cette partie est de vérifier que l'angle de tangage fourni par la centrale est cohérent avec celui que nous allons calculer à l'aide des accéléromètres et de la vitesse de tangage.

Dans le fichier \(\texttt{ simulateur.py}\), le fichier \(\texttt{ data.txt}\) est lu, puis un certain nombre de vecteurs de données sont extraits temps, tangage, ...

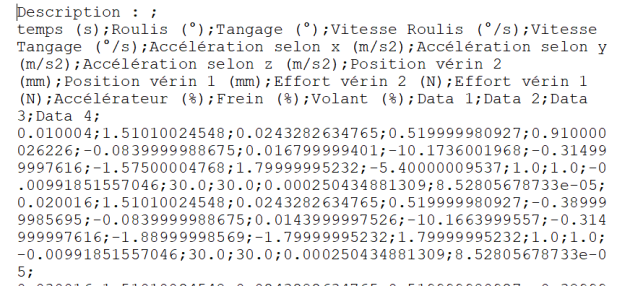
Le script Python précédent permet de récupérer les données suivantes contenu dans le fichier de mesures sous forme de listes :