Introduction
Dérivation numérique :
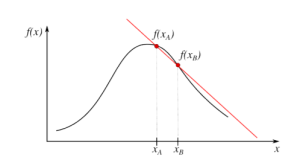
Définition mathématique : \(f'(x_0)=\lim_{x\rightarrow x_0}\frac{f(x)-f(x_0))}{x-x_0}\)
cette formulation est équivalente à \(f'(x_0)=\lim_{h\rightarrow 0}\frac{f(x_0+h)-f(x_0))}{h}\)
Cela revient simplement au calcul d'une pente d'une droite :
\(\frac{f(x)-f(x_0))}{x-x_0}=\frac{f(x)-f(x_0))}{x-x_0}\) ressemble à \(\frac{f(x_B)-f(x_B))}{x_B-x_A}\)
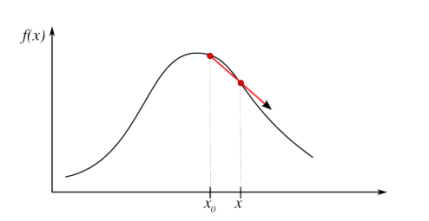
En utilisant le développement de Taylor : \(f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2 !}(x-a)^2+....\)
A l'ordre un on retrouve \(f(x)=f(a)+f'(a)(x-a)\)
Remarque :
Lorsqu’on cherche la dérivé de \(f(x)\) en \(x_0\) on a plusieurs options :
on peut calculer \(f'(x_0)=\frac{f(x_0+h)-f(x_0)}{h}\), \(f'(x_0)=\frac{f(x_0)-f(x_0-h)}{h}\) où encore \(f'(x_0)=\frac{f(x_0+h /2)-f(x_0-h /2)}{h}\)
on parle alors de dérivation à gauche, à droite où centrée.
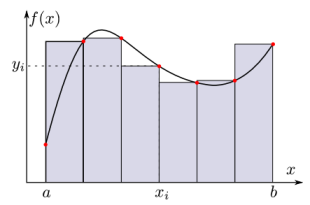
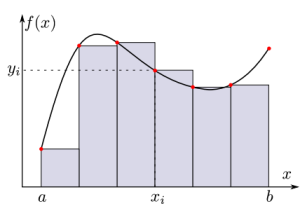
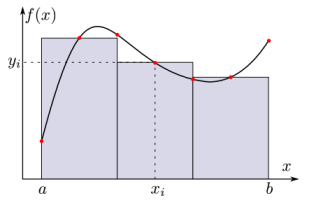
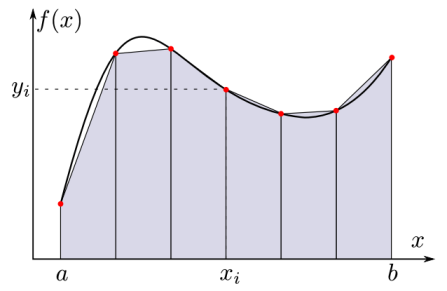
Intégration numérique :
L'intégration numérique consiste à intégrer (de façon approchée) une fonction sur un intervalle borné \([a, b]\), c'est-à dire-calculer l'air sous la courbe représentant la fonction, à partir d'un calcul ou d'une mesure en un nombre fini de point \((x_i, y_i)\).
