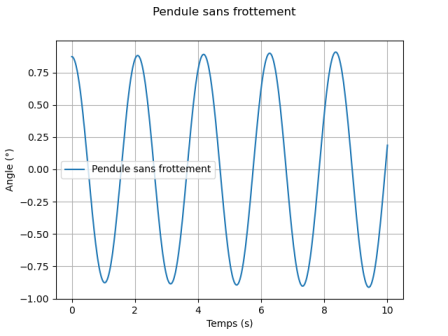
Pendule sans frottement

Pour résoudre cette équation, on retient un schéma d'Euler explicite. On observe l'évolution de l'angle sur une durée de 5 périodes environ. On discrétise le temps total en un grand nombre de pas de temps \(h\) (au moins 2000).

La position initiale est prise égale à \(10^{\circ}\)

Question

Définir sur feuille la fonction \(\dot X = F(X,t)\) ici \(F(thet,thetp,t)\) (sans linéariser) pour le problème du pendule simple et proposer une implantation de cette fonction en Python. Écrire une fonction \(\tt F1(thet,thetp)\) sur Python renvoyant le résultat ci-dessus.

Indice

On a : \(m_1 L_1 \ddot \theta_1 + m_1 g \sin\theta_1 = 0\)

Pour résoudre ce problème, on se ramène à un problème de Cauchy d'ordre 1 : \(\dot X = F(X,t)\).

On a alors le système différentiel suivant : \(\left\{\begin{array}{ll}V(t)=\dot \theta_1(t) \\\dot V=-\frac{ g \sin\theta_1}{L_1} \end{array}\right.\)

On cherche à écrire une fonction \(\tt F1(thet,thetp)\) qui renvoie \(V(t)\) et \(\dot V\).

Solution

1
def F1(thet,thetp):
2
    V=thetp
3
    Vp=-g/L1*sin(thet)
4
    return V,Vp

Question

Écrire une fonction \(\tt euler2(f,theta0,theta0p)\) algorithme d'Euler pour résoudre cette équation différentielle du second ordre.

Tester l'algorithme avec les conditions initiales données et tracer l'évolution de l'angle au cours du temps.

Indice

Solution

1
def euler2(f,theta0,thetap0):
2
    ang=[theta0]
3
    vit=[thetap0]
4
    for i in range(len(t)-1) :
5
        tmptheta,tmpthetap = f(ang[i],vit[i],t[i]) #
6
        angc=ang[i]+pas*tmptheta
7
        vitc=vit[i]+pas*tmpthetap
8
        ang.append(angc)
9
        vit.append(vitc)
10
    return ang,vit

Pour vérifier le tracé, il est intéressant de chercher une solution analytique du problème. Celle-ci n'est pas facile à déterminer dans le cas général. Cependant, si on choisit des valeurs initiales de l'angle de lâcher petites, l'équation différentielle peut se simplifier.

Question

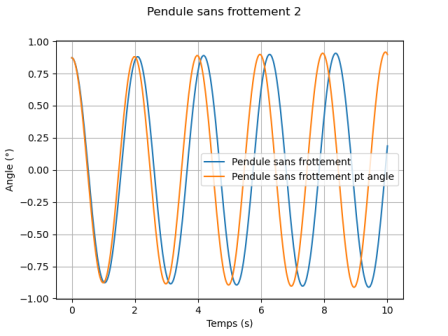
Proposer une simplification de l'équation différentielle dans le cas où l'angle \(\theta\) est petit, déterminer alors analytiquement la solution temporelle et superposer cette solution à la solution obtenue numériquement.

L'écrire sur Python, on l'appellera \(\tt F2(thet,thetp)\).

Déterminer la pertinence de la simplification réalisée en testant différentes valeurs initiales.

Indice

Comparaison solution en sinus et pt angle ici 50° ! !

Solution

1
# Pour linéariser, on suppose sin(theta) = theta
2
def F2(thet,thetp):
3
    theta=thetp
4
    thetap=-g/L1*(thet)
5
    return theta,thetap