Présentation du contexte de l'étude pour ordre 2 : Étude mécanique d'un pendule
Objectif
Tracer la réponse d'une équation différentielle d'ordre 2
Présentation
On considère dans un premier temps un modèle simple de pendule constitué d'une tige sans masse de longueur \(L_1 = 1~m\) et d'une masse \(m_1 = 1~~kg\) à l'extrémité \(A\) de la barre \(1\).
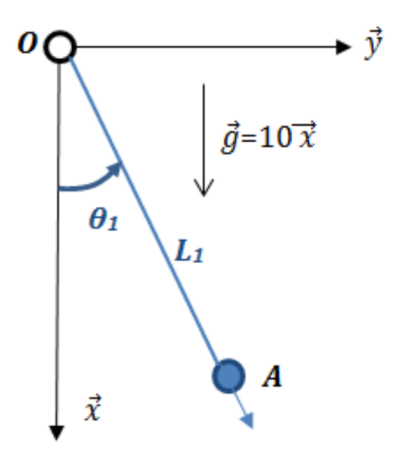
Sans frottement
En supposant qu'il n'y a pas de frottement, le principe fondamental de la dynamique appliqué à la masse ponctuelle permet d'aboutir à l'équation suivante : \(m_1 L_1 \ddot \theta_1 + m_1 g \sin\theta_1 = 0\)
On écarte initialement la masse d'un angle \(\theta_1(0)=\theta_{10}\) donné et on la lâche à une vitesse nulle \(\dot\theta_1(0)=0\).
Avec frottement
On considère désormais que les frottements dans la liaison pivot ne sont plus négligeables. Ceux-ci sont modélisés comme des frottements secs. Les forces de frottements dans l'air sont modélisées par une force proportionnelle à la vitesse (frottement visqueux).
Avec toutes ces considérations, l'équation différentielle à résoudre est : \(m_1 L_1 \ddot \theta_1 + \mu L_1 \dot{\theta_1} + m_1 g \sin\theta_1 + f(\theta_1) = 0\)
avec \(\mu=0.4~N.s/m\) coefficient de frottement visqueux.
La fonction \(f(\theta_1)\) modélise la force de frottement sec et dépend du signe de la vitesse angulaire (lois de Coulomb) :
\(f(\theta_1)=f_1\) si \(\dot{\theta_1} >= 0\)
\(f(\theta_1)=-f_1\) si \(\dot{\theta_1} < 0\)
avec \(f_1=0.05~~N\)