Présentation du contexte de l'étude pour ordre 1 : Asservissement en vitesse d'un chariot
Objectif
Tracer la réponse d'une équation différentielle d'ordre 1
Présentation
Considérons le contrôle en vitesse du mouvement d'un chariot de technologie analogue à ceux situés sur les pistes d'athlétisme afin de suivre et filmer les coureurs. Ce chariot est alimenté par une tension électrique. La grandeur de sortie est la vitesse de translation.

En boucle ouverte
Le comportement temporel du chariot soumis à une tension de commande est modélisé par une équation différentielle du premier ordre : \(\tau_c \frac{d v(t)}{dt} + v(t)= K_c u_c(t)\)
L'objectif est d'obtenir la réponse temporelle du système à une entrée échelon (entrée constante) \(u_c(t)=U_{mot}\).
On prendra \(U_{mot}=5V\), \(\tau_c=1s\) et \(K_c=0,5~m.s^{-1}V^{-1}\).
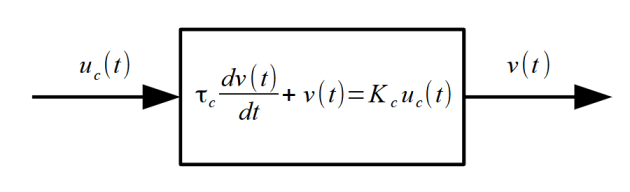
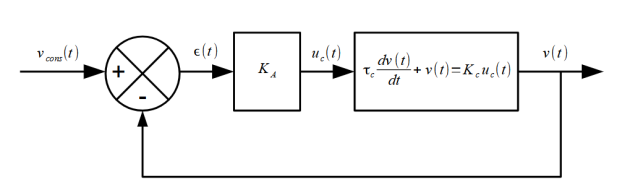
En boucle fermée
Afin de contrôler le chariot, le pilotage s'effectue en boucle fermée. Une consigne de vitesse \(v_{cons}(t)\) est imposée égale à \(6~~m.s^{-1}\). Cette consigne est comparée à la vitesse du chariot \(v(t)\). L'écart générée est adaptée par un gain réglable \(K_A,\) soit \(u_c(t)=K_A\epsilon(t)\).
On prendra \(K_A=0,5~m.s^{-1}V^{-1}\).
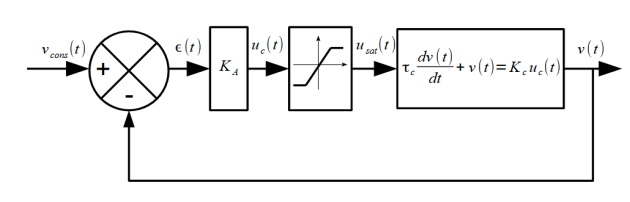
Avec prise en compte de la saturation
Le choix d'un gain \(K_A\) élevé permet de gagner en précision et rapidité. Toutefois, la tension d'alimentation du chariot est écrêtée à +12V ou -12V. Il faut donc en tenir compte dans notre modélisation par une saturation. \(u_{max}=12 V\).