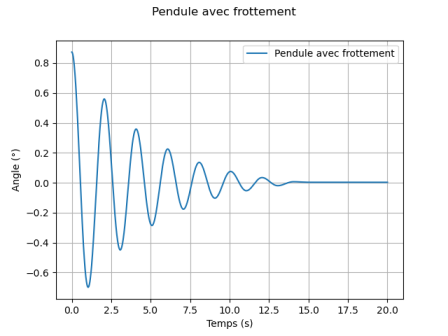
Pendule avec frottements secs et fluides
Question
Définir la nouvelle fonction \(F3(X,t)\) pour modéliser cette équation différentielle.
Tester votre implantation pour différents angles initiaux, on prendra un pas de l'ordre de \(10^{-2}\).
Indice
On a \(m_1 L_1 \ddot \theta_1 + \mu L_1 \dot{\theta_1} + m_1 g \sin\theta_1+ f(\theta_1)=0\).
Pour résoudre ce problème, on se ramène à un problème de Cauchy d'ordre 1 : \(\dot X = F(X,t)\).
On a alors le système différentiel suivant : \(\left\{\begin{array}{ll}V(t)=\dot \theta_1(t) \\\dot V=-\frac{ 1}{m_1 L_1}(\mu L_1 V + m_1 g \sin\theta_1+ f(\theta_1)) \end{array}\right.\)
On cherche à écrire une fonction \(\tt F1(thet,thetp)\) qui renvoie \(V(t)\) et \(\dot V\).
On a deux cas, si \(\dot{\theta_1} >= 0\) on a alors \(\left\{\begin{array}{ll}V(t)=\dot \theta_1(t) \\\dot V=-\frac{ 1}{m_1 L_1}(\mu L_1 V + m_1 g \sin\theta_1- f_1)) \end{array}\right.\)
Solution
def F3(thet,thetp):
if thetp >=0:
V=thetp
Vp=-g/L1*sin(thet)-mu/m1*V-0.05/(L1*m1)
return V,Vp
else:V=thetp
Vp=-g/L1*sin(thet)-mu/m1*V+0.05/(L1*m1)
return V,Vp