Étude en boucle fermée
Avec le schéma-bloc on a la même équation différentielle que précédemment à résoudre simplement \(u_c(t)=K_A\epsilon(t)\) avec \(\epsilon(t)= v_{cons}(t)-v(t)\).
Question
Écrire une fonction \(\tt ordre1\_BF(vc,temps)\) renvoyant une liste d'ordonnées correspondant à la résolution par la méthode d'Euler explicite du système en boucle fermée
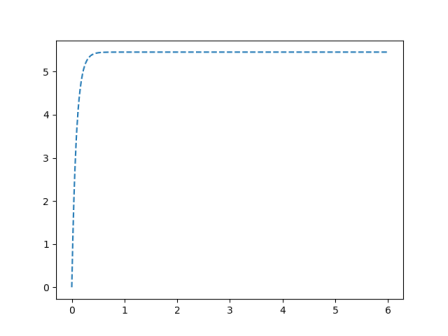
Tracer la réponse du système pour une vitesse de consigne constante\( v_{cons}(t)=6m.s^{-1}\) et un gain d'adaptation \(K_A=20 V.s.m^{-1}\).
Solution
1
def ordre1_BF(vc,temps):
2
s=0
3
sortie=[0]
4
for i in range(1,len(temps)):
5
u=K_a*(vc-s)
6
f=(K_c*u-s)/tau_c
7
s=s+f*(temps[i]-temps[i-1])
8
sortie=sortie + [s]
9
return sortie
10
11
12
#Le tracé13
x=liste_temps(tmax,pas)
14
y=ordre1_BF(V_c,x)
15
plt.plot(x,y,'--')
16
plt.show()