Modélisation MCC simplifiée
Modèle de connaissance
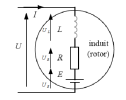
On rappelle que les équations du moteur à courant continu sont :
équation électrique : \(u_m(t) = e_m(t) + R_m i(t) + L_m \frac{di(t)} {dt}= e_m(t) + R_m i(t) \) avec \(L_m\) négligeable.
équations de couplage :\( e_m(t) = k \omega_m(t)\) et \( C_m(t) = k i(t)\)
équation mécanique : \( J \frac{ \omega_m(t)}{dt}=C_m(t)- C_r(t)\)
où \(J\) appelée inertie équivalente ramenée sur l'arbre moteur,
\(C_m(t)\) et \(C_r(t) \) sont des couples (actions mécaniques en N.m ayant tendance à mettre en rotation un solide).

Écriture des fonctions de transfert :
On écrira alors \(\Omega_m(p)=H_1(p)U_m-H_2(p)C_r\) avec \(H_1(p)=\frac{\frac{1}{k}}{\frac{JR}{k^2}p+1}\) ett \(H_2(p)=\frac{\frac{R}{k^2}}{\frac{J_{eq}R}{k^2}p+1}\).
Dans certain cas on pourra aussi supposer que \(C_r(t) \) couple résistant est négligeable.
Modèle de comportement
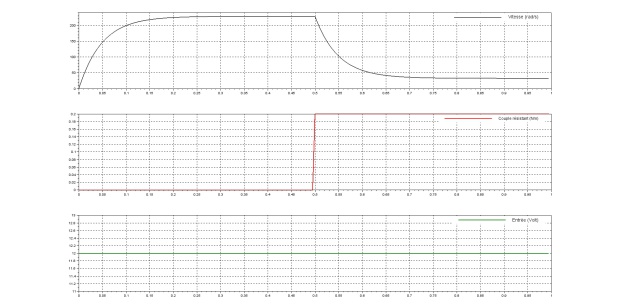
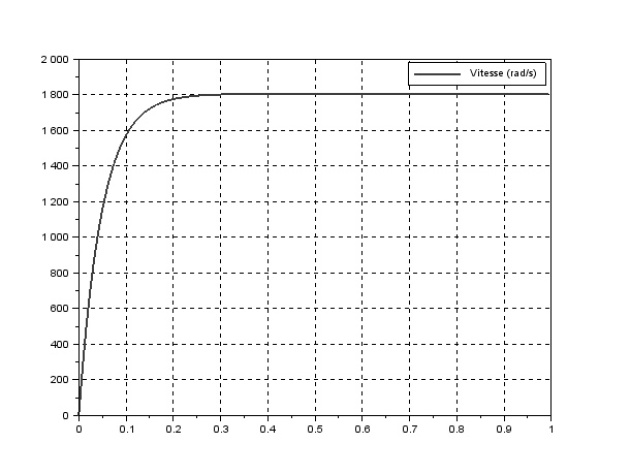
En prenant des caractéristiques de moteur dans une documentation constructeur on trace les réponses suivantes : (f=0)
On retrouve ce qu'on avait avec le modèle de connaissance, on peut ramener ce modèle à un modèle du premier ordre, ce qui revient à dire que L l'inductance est négligeable ;
Dans certain cas on pourra aussi supposer que \(C_r(t) \) couple résistant est négligeable.
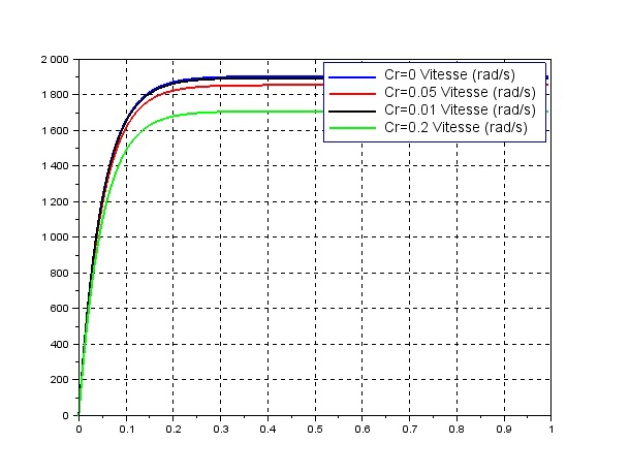
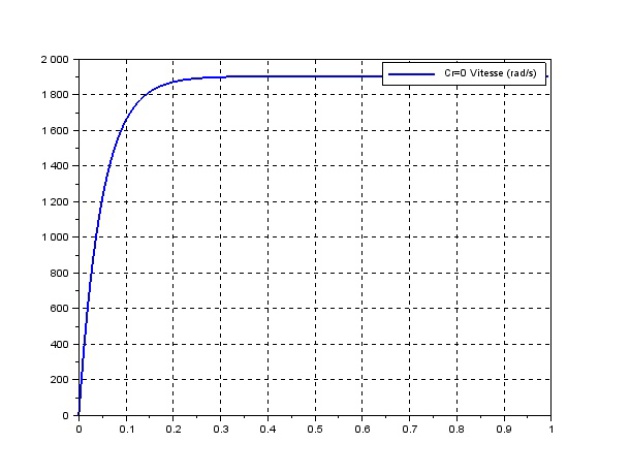
Modèle de comportement : moteur en BO sans couple résistant \(C_r(t)=0 \)
On a \({\Omega_m(p)} =H_1(p)U_m(p) \) avec une identification classique d'un premier ordre si l'entrée est en échelon...
Modèle de comportement : moteur en BO avec couple résistant \(C_r(t) \)
Équation générale : \({\Omega_m(p)} =H_1(p)U_m(p) – H_2(p)C_r(p)\). Avec \(H_1(p)=\frac{K_m}{1+\tau_m.p}\) et \(H_2(p)=\frac{K_p.(1+...)}{1+\tau_m.p}\) les différentes constantes étant fonction des paramètres du moteur.
La valeur finale est donc plus basse que celle attendue sans couple résistant. Il faut alors réaliser plusieurs essais en variant la consigne puis tracer la droite tel que \({\Omega_m\infty} =K_mU_0 – K_pC_{r0}\).