Composants du labo

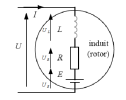
On rappelle que les équations du moteur à courant continu sont :

• équation électrique : \(u(t) = e_m(t) + R i(t) + L \frac{di(t)} {dt} \)

• équations de couplage :\( e_m(t) = k_e \omega_m(t)\) et \( C_m(t) = k_m i(t)\) (on fait généralement l'hypothèse \(k_e = k_m\)).

• équation mécanique : \( J_{eq} \frac{ \omega_m(t)}{dt}=C_m(t)- C_r(t)-f \omega_m(t)\)

  • où \(J_{eq}\) appelée inertie équivalente ramenée sur l'arbre moteur,

  • \(f\) coefficient de viscosité

  • \(C_m(t)\) et \(C_r(t) \) sont des couples (actions mécaniques en N.m ayant tendance à mettre en rotation un solide).

Cette équation mécanique :

- suppose que le moteur soit monté dans un système à une mobilité, dans le cas général \(C_r(t)\) peut dépendre de la position et de la vitesse de façon non linéaire...

- provient d'un TEC appliqué à l'ensemble en mouvement, toute le actions 'motrice sont regroupées dans \(C_m\) et les 'résistantes' dans \(C_r\).

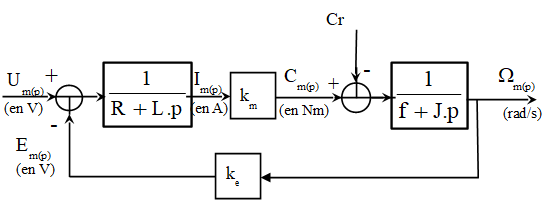
Écriture des fonctions de transfert :

Le passage dans le domaine de Laplace suppose que l'équation mécanique soit linéaire. On a alors \(\Omega_m(p)=\frac{k_m}{(J_{eq}p+f)(Lp+R)+k_mk_e}U_m-\frac{(Lp+R)}{(J_{eq}p+f)(Lp+R)++k_mk_e}C_r\).

Remarques avant étude :

Une étude numérique de cette fonction (avec les caractéristiques des moteurs à courants continu ) permet de se ramener à un modèle où L l'inductance est négligeable ;

Dans la grande majorité des systèmes étudiés f=0 (frottement fluide ! !)

Par construction du moteur \(k_m=k_e\) on les notera simplement \(k\)

Soit alors \(\Omega_m(p)=\frac{k}{J_{eq}Rp+k^2}U_m-\frac{R}{J_{eq}Rp+k^2}C_r\). On écrira alors \(\Omega_m(p)=H_1(p)U_m-H_2(p)C_r\) avec \(H_1(p)=\frac{\frac{1}{k}}{\frac{J_{eq}R}{k^2}p+1}\) et \(H_2(p)=\frac{\frac{R}{k^2}}{\frac{J_{eq}R}{k^2}p+1}\). On constate qu'on a alors deux relations du premier ordre avec \(K_1=1/k\), \(K_2=R/k^2\) et \(\tau_m=\frac{J_{eq}R}{k^2}\).

Dans certain cas on pourra aussi supposer que \(C_r(t) \) couple résistant est négligeable.

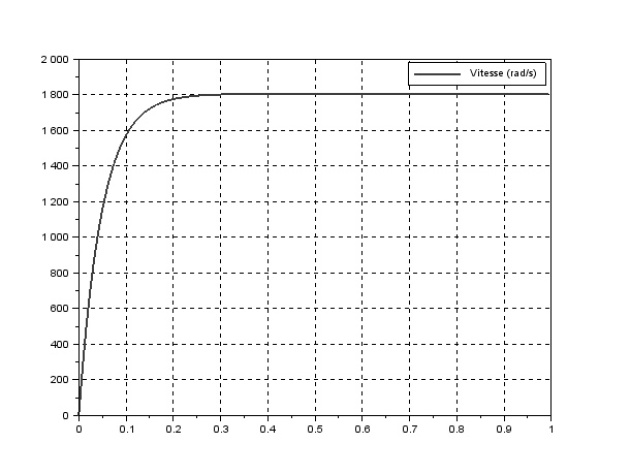
En prenant des caractéristiques de moteur dans une documentation constructeur on trace les réponses suivantes : (f=0)

On retrouve ce qu'on avait avec le modèle de connaissance, on peut ramener ce modèle à un modèle du premier ordre, ce qui revient à dire que L l'inductance est négligeable ;

• Dans certain cas on pourra aussi supposer que \(C_r(t) \) couple résistant est négligeable.

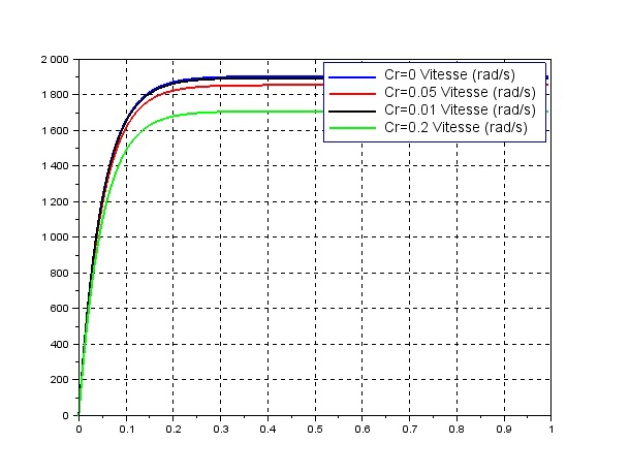
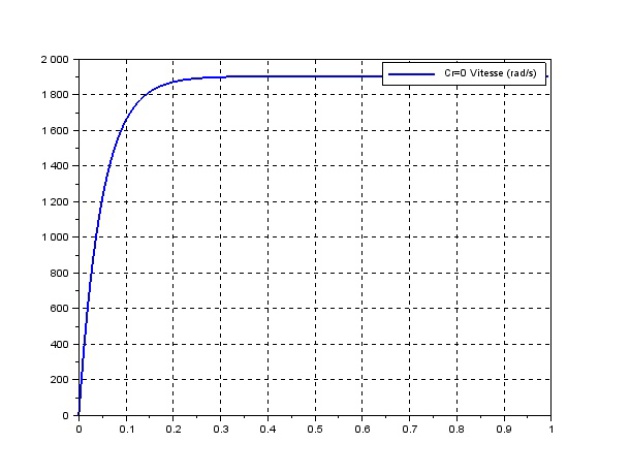
Modèle de comportement : moteur en BO sans couple résistant \(C_r(t)=0 \)

On a \({\Omega_m(p)} =H_1(p)U_m(p) \) avec une identification classique d'un premier ordre si l'entrée est en échelon...

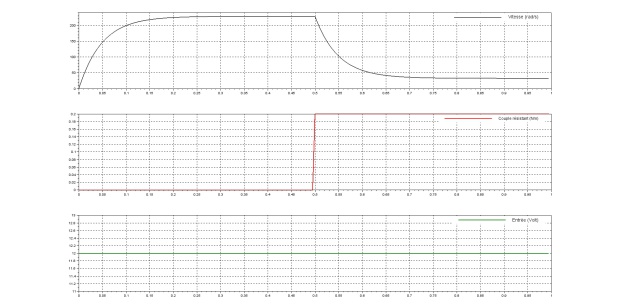
Modèle de comportement : moteur en BO avec couple résistant \(C_r(t) \)

Équation générale : \({\Omega_m(p)} =H_1(p)U_m(p) – H_2(p)C_r(p)\). Avec \(H_1(p)=\frac{K_m}{1+\tau.p}\) et \(H_2(p)=\frac{K_p.(1+...)}{1+\tau_m.p}\) les différentes constantes étant fonction des paramètres du moteur.

La valeur finale est donc plus basse que celle attendue sans couple résistant. Il faut alors réaliser plusieurs essais en variant la consigne puis tracer la droite tel que \({\Omega_m\infty} =K_mU_0 – K_pC_{r0}\).