Composants du labo

Rappel des équations détaillées dans la partie modélisation : \(\Omega_m(p)=H_1(p)U_m-H_2(p)C_r\)

On se placera dans des conditions d'essai où \(C_r=0\) soit \(\Omega_m(p)=\frac{k}{J_{eq}Rp+k^2}U_m=\frac{\frac{1}{k}}{\frac{J_{eq}R}{k^2}p+1}\).

On constate qu'on a un premier ordre avec \(K_1=1/k\), et \(\tau=\frac{J_{eq}R}{k^2}\).

L'identification d'un MCC revient à trouver \(K_1\) et \(\tau\).

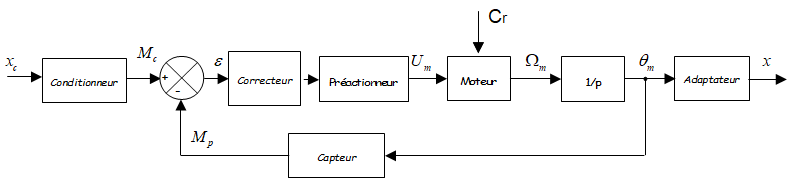
Dans le cas général on peut avoir un asservissement du type :

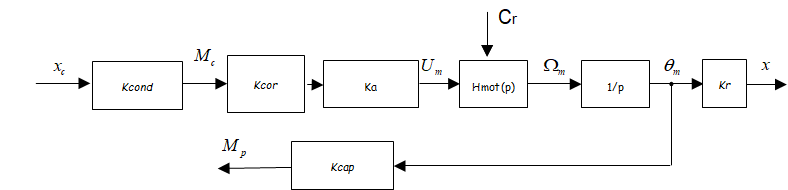
Le correcteur peut-être choisi proportionnel, le préactionneur, l'adaptateur et le capteur sont aussi proportionnel. De plus le conditionneur se déduit des précédent et est lui aussi proportionnel , on a alors le schéma suivant :

Pour réaliser une identification temporelle il faut connaître et maîtriser l'entrée envoyée au système, classiquement un échelon, sur un système asservi cela nécessite de pouvoir faire un essai en BO en effet si la boucle de retour n'est pas débrancher une entrée en \(x_c\) en échelon n'assure pas que le moteur soit sollicité par un échelon : \(U_m=K_aK_c(x_c-\frac{K_{cap}}{Kr}x)\) avec x variable ! ! !

De plus l'identification n'est possible que si \(C_r \) est constant.

Essai en BO :

Imaginons que le logiciel permet d'envoyer un échelon de consigne \(U_m=U_0\) et qu'il permette de tracer :

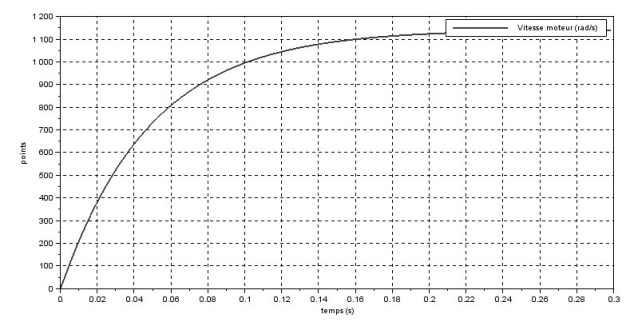
• 1. la vitesse de rotation \({\Omega_m(p)}\),

• 2. uniquement le nombre de points en sortie du codeur \(M_p\).

1. la vitesse de rotation \({\Omega_m(p)}\).

Recherche de \(K_1\) et \(\tau_m\) :

Dans tous les cas \(\tau\) se déduit de la courbe avec les méthodes classique pour le premier ordre.

La valeur asymptotique de \(\Omega_m\) est égale à : \({\Omega_{m\infty}=K_{1}X_{c0}}\).

Certains logiciels permettent d'envoyer l'échelon de consigne en \(X_c\) ou \(M_c\) il faut alors ajouter les gain associés dans l’équation, on a respectivement :

• \(\Omega_{m\infty}=K_{cond}K_{cor}K_aK_{1}X_{c0}\).

• \({\Omega_{m\infty}=K_{cor}K_aK_{1}M_{c0}}\).

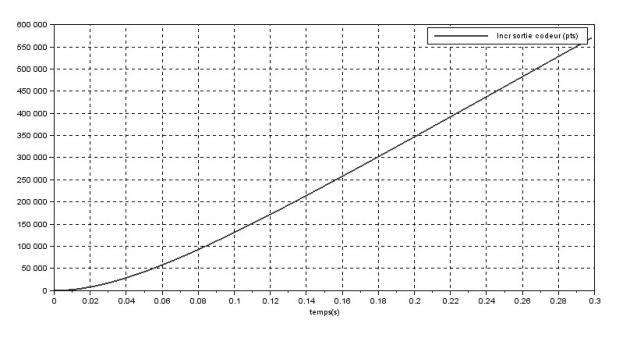
2. le nombre de points en sortie du codeur \(M_p\) .

On a \(M_p=K_{cap}\frac{1}{p} H_{mot}(p)\frac{U_{0}}{p}=\frac{U_{0}}{p^2} K_{cap}H_{mot}(p) \) soit la réponse d'un premier ordre à une rampe.

Rappel : pour une rampe la réponse est d'équation temporelle : \(s(t)=Ke_0(t-\tau+\tau.e^{\frac{t}{\tau}})\) qu'on retrouve en intégrant la réponse à un échelon avec des conditions initiales nulles.

On peut alors identifier :

• la gain statique donne \(K_{1}\) avec la pente de l'asymptote à l'infini.

• la constante de temps \(\tau\) avec l'intersection entre l'axe des abscisse et l'asymptote à l'infini.

Lorsqu'on lance un essai sur le système bouclé précédent, si \(X_{c}\) est un échelon alors \(U_{m}\) est un sinus amorti, dans ce cas l'identification est impossible car en entrée du moteur on a pas une fonction test classique.

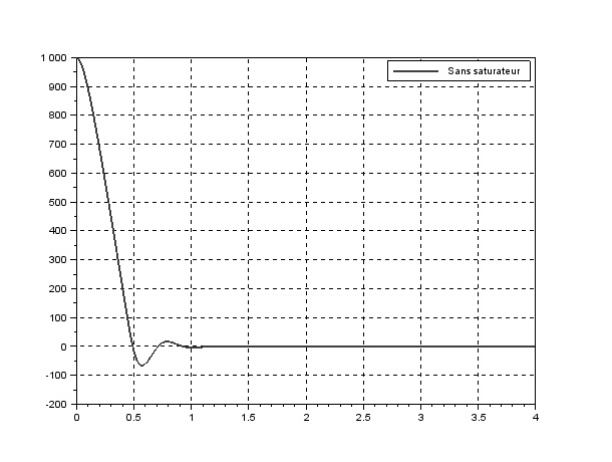
On utilise alors le dispositif de protection du moteur, un saturateur situé avant le moteur qui limite la valeur de \(U_{m}\) , pour être dans ces conditions mettre un correcteur proportionnel avec un \(K_{p}\) le plus grand possible.

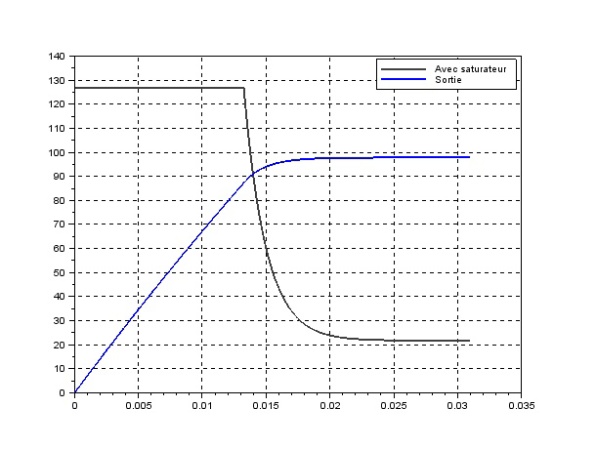
Pendant tout le temps ou le saturateur "fonctionne" la moteur voit un entrée en échelon égale à la tension de saturation, on peut alors identifier la fonction du moteur. On se ramène donc au cas classique.