Introduction
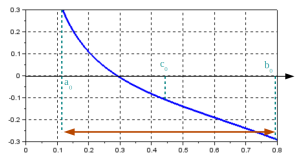
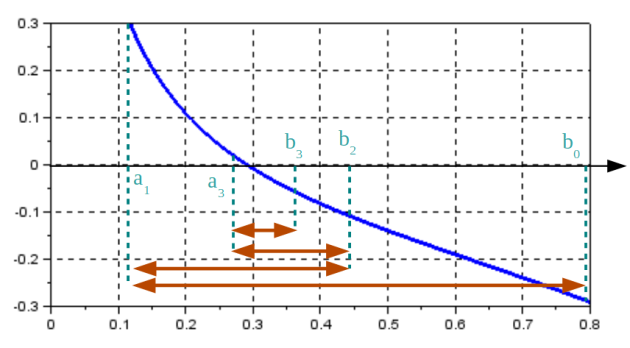
Méthode par dichotomie
\(f\) continue sur un intervalle \([a, b]\) tel \(f(a)f(b) < 0\)
Théorème des valeurs intermédiaires : il existe au moins un 0 sur \([a,b]\)
On coupe l'intervalle \([a,b]\) en deux parties égales et on regarde sur quel intervalle se trouve la racine \(c = \frac{(a+b)} { 2}\) et on teste :
\(f(a)f(c) < 0\) : la racine est sur \([a,c]\) alors on prend \(b = c\)
Sinon la racine est sur \([b,c]\) alors on prend \( a = c\)
On itère jusqu'à convergence
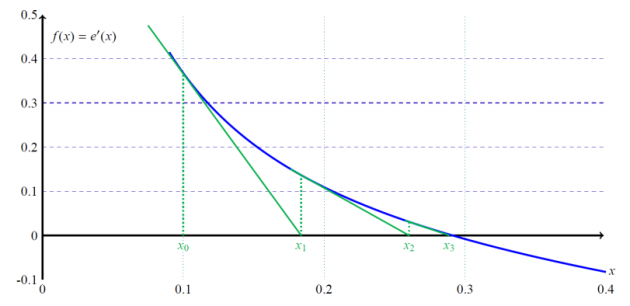
Méthode par Newton
En utilisant le développement de Taylor : \(f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2 !}(x-a)^2+....\)
A l'ordre un on retrouve \(f(x)=f(a)+f'(a)(x-a)\)
À partir d'un point \( x_0\), la méthode consiste à rechercher le point suivant \(x_1\) en le supposant racine de la fonction dans le développement de Taylor à l'ordre 1.
\(0=f(x_1)=f(x_0)+f'(x_0)(x_1-x_0)\) soit directement \(x_1=x_0-\frac{f(x_0)}{f'(x_0}\)
Soit \( f\) de classe \(C^1\) sur\( I = [a, b]\) :
– Initialisation : Choisir un premier candidat \(x_0\) dans l'intervalle \(I\)
– Hérédité : calculer \( x_{n+1}=x_{n}-\frac{f(x_n)}{f'(x_n)}\)
– Test d'arrêt : Tester le critère de convergence \(|f (x_n+1)| < \varepsilon\) et \(\varepsilon\) choisit très petit.