Stabilisateur cardiaque actif
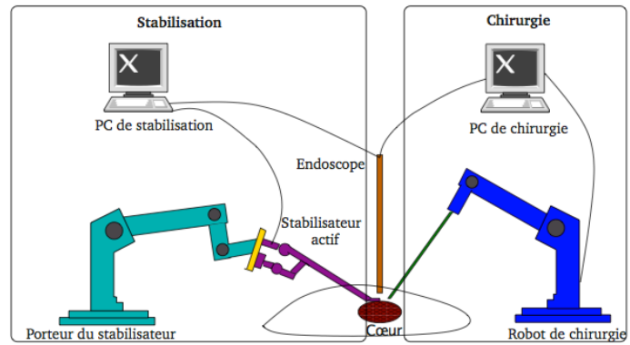
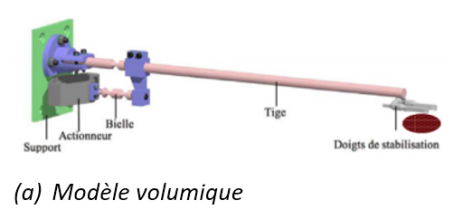
Les pathologies cardiaques, et particulièrement les rétrécissements des artères qui alimentent le myocarde (muscle cardiaque), sont en constante augmentation. La chirurgie à cœur battant se substitue progressivement à celle courante impliquant un arrêt du cœur et la mise en place d'une circulation extracorporelle. L'avantage essentiel de cette chirurgie à cœur battant est de limiter les complications induites par l'intervention. Cette technique opératoire se différencie du pontage classique par la conservation du battement cardiaque durant l'intervention ; la principale difficulté réside alors dans la nécessité d'immobiliser la partie du cœur à opérer. L'objet de l'étude proposée concerne un stabilisateur cardiaque actif, c'est à dire piloté en position afin d'immobiliser la zone cible.
une tige flexible (5) de diamètre compatible avec la chirurgie mini‐invasive comportant à son extrémité une fixation par succion sur la paroi cardiaque ;
un dispositif bielle‐manivelle constitué de liaisons obtenues par enlèvement de matière et modélisées par des liaisons pivots élastiques (sans jeu) ;
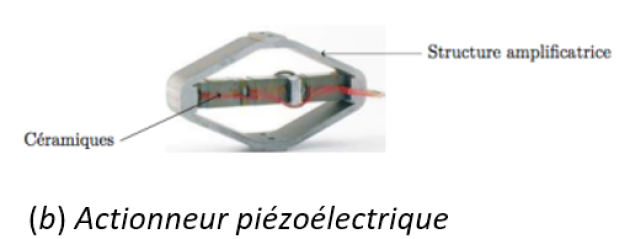
un actionneur linéaire piézoélectrique afin de garantir une dynamique importante. L'accélération du myocarde (le muscle cardiaque) passe de \(0,25 m \cdot {s^{ - 2}}\) (avec stabilisateur) à \(10 m \cdot {s^{ - 2}}\) (sans stabilisateur). Le déplacement maximal de l'actionneur est obtenu par une structure amplificatrice et vaut \(130 \mu m\).
Dans le cadre de l'étude, les hypothèses et données suivantes sont à prendre en compte :
l'étude envisagée est faite dans le cadre d'une modélisation plane. Le repère \(\left( {O,\overrightarrow {{x_0}} ,\overrightarrow {{y_0}} ,\overrightarrow {{z_0}} } \right)\) est lié au bâti et supposé galiléen.
les solides sont considérés indéformables y compris la tige (5).
la tige (5) est assimilée à un cylindre plein dont le diamètre \({D_5} = 10 mm\) est négligeable devant la longueur \({L_5} = 300 mm\). Sa masse est \({m_5} = 185g.\)
les masses et inerties des autres pièces sont négligées.
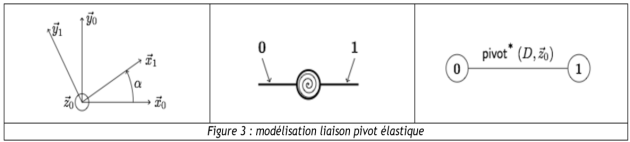
Les liaisons élastiques sont modélisées par des liaisons pivots parfaites auxquelles s'ajoute de manière indissociable une raideur de torsion générant un couple de rappel porte par l'axe de la liaison. Ces liaisons seront notées pivot *. Ainsi, par exemple, la liaison pivot * entre les solides (0) et (1) peut être représentée comme la superposition d'une liaison pivot parfaite et d'un ressort de torsion monté entre (0) et (1), de raideur \({K_{01}}\). On obtient alors par exemple, le graphe et le schéma cinématique associée à cette liaison pivot *.
Les déplacements envisagés sont de petits déplacements. Dans toute la suite, et pour des petites valeurs d'un angle\( \beta\) défini en radians, \({\rm{\;sin\;}}\beta = \beta\) et \({\rm{\;cos\;}}\beta = 1\).
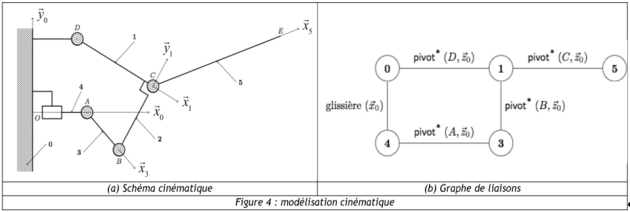
Un modèle cinématique du stabilisateur actif est défini ci-dessous :
Le stabilisateur actif possède deux degrés de liberté :
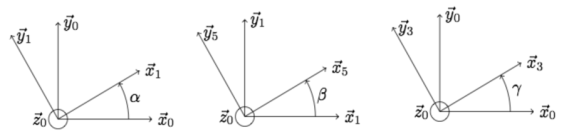
Le premier est relatif à la translation de l'actionneur piézoélectrique et contrôle la rotation \(\alpha = \left( {\overrightarrow {{x_0}} ,\overrightarrow {{x_1}} } \right) = \left( {\overrightarrow {{y_0}} ,\overrightarrow {{y_1}} } \right)\), angle de rotation de (1) par rapport à (0).
Le second est relatif à la rotation \(\beta = \left( {\overrightarrow {{x_1}} ,\overrightarrow {{x_5}} } \right) = \left( {\overrightarrow {{y_1}} ,\overrightarrow {{y_5}} } \right)\) de la tige (5) par rapport au solide (1). Cette rotation n'est pas directement pilotée.
Les données géométriques sont les suivantes :
\(\overrightarrow {OA} = \lambda \overrightarrow {{x_0}}\) ; \(\overrightarrow {DC} = {L_1}\overrightarrow {{x_1}}\) ; \(\overrightarrow {CB} = - {d_1}\overrightarrow {{y_1}}\) ; \(\overrightarrow {OA} = \lambda \overrightarrow {{x_0}}\) ;
\(\overrightarrow {BA} = - {L_3}\overrightarrow {{x_3}}\) ; \(\overrightarrow {CE} = {L_5}\overrightarrow {{x_5}}\) ; \(\overrightarrow {OD} = a\vec x + {d_1}\overrightarrow {{y_0}}\).
Afin de mettre en place un asservissement des angles \(\alpha\) et \(\beta\), il est nécessaire de déterminer les équations de comportement dynamique de ce système. Une des équations est obtenue par application du théorème du moment dynamique au solide (5) au point C et en projection sur l'axe \(\overrightarrow {{z_0}}\) , ce qui impose le calcul du moment dynamique galiléen de la tige (5) au point C en projection sur la direction \(\overrightarrow {{z_0}\;}\) . L'objectif de l'étude proposée est de déterminer les quantités cinétiques et dynamiques nécessaires à l'obtention de cette équation.
Question
Q1. Monter que le moment d'inertie \( {I_5}\) de la tige (5) par rapport à l'axe \( \left( {C,\overrightarrow {{z_0}} } \right)\) s'exprime par \({I_5} = {m_5}\frac{{L_5^2}}{3}\).
Solution
Matrice inertie d'un cylindre en G de révolution autour de l'axe \(\left( {G,\overrightarrow {{x_5}} } \right)\)
\(\bar I\left( G \right) = {\left[ {\begin{array}{*{20}{l}}{{A_1}}&0&0\\0&{{B_1}}&0\\0&0&{{B_1}}\end{array}} \right]_S}\) avec \({A_1} = {\rm{m}}\frac{{{R^2}}}{2}\) et \({B_1} = {\rm{m}}\left( {\frac{{{R^2}}}{4} + \frac{{{h^2}}}{{12}}} \right)\)
Pour une tige on a alors R = 0
Ici pour le solide 5 en \({G_5}\) on a alors \\( I\left( {{G_5},5} \right) = {\left[ {\begin{array}{*{20}{l}}0&0&0\\0&{{{\rm{m}}_5}\frac{{L_5^2}}{{12}}}&0\\0&0&{{{\rm{m}}_5}\frac{{L_5^2}}{{12}}}\end{array}} \right]_{\overrightarrow {{x_5}} ,\overrightarrow {{y_5}} ,\overrightarrow {{z_0}} }}\)
Le terme qui nous intéresse est en \( \overrightarrow {{z_0}}\) avec Huygens on peut écrire :
\({I_5} = {m_5}\frac{L_5^2}{12} + {m}_5\frac{L_5^2}{4}={m_5}\frac{L_5^2}{3}\)
Question
Q2. Montrer que le moment cinétique galiléen de la tige (5) au point C et en projection sur \({\vec z_0}\) est donné par :\( \overrightarrow {{\sigma _{C,5/0}}} \;\overrightarrow {.{z_0}} = {m_5}\left( {\frac{{L_5^2}}{3} + \frac{{{L_5}{L_1}}}{2}} \right)\dot \alpha + {m_5}\frac{{L_5^2}}{3}\dot \beta\)
Solution
\(\overrightarrow {{\sigma _{C,5/0}}} \;.\overrightarrow {{z_0}} = \left( {{m_5}\;.\;\overrightarrow {C{G_5}} \wedge \overrightarrow {{V_{C,5/0}}} + \left[ {I\left( {C,5} \right)} \right]\overrightarrow {{\Omega _{5/0}}} } \right).\overrightarrow {{z_0}}\)
\(\overrightarrow {{\sigma _{C,5/0}}} \;.\overrightarrow {{z_0}} = {m_5} \cdot \left( {\frac{{{L_5}}}{2}\overrightarrow {{x_5}} \wedge {L_1}\dot \alpha \overrightarrow {{y_1}} } \right).\overrightarrow {{z_0}} + {m_5}\frac{{L_5^2}}{3}\left( {\dot \alpha + \dot \beta } \right) = {m_5}\frac{{{L_5}{L_1}}}{2}\dot \alpha {\rm{\;cos\;}}\left( \beta \right) + {m_5}\frac{{L_5^2}}{3}\left( {\dot \alpha + \dot \beta } \right)\)
Avec les hypothèses sur les petits angles : \(\overrightarrow {{\sigma _{C,5/0}}} \;.\overrightarrow {{z_0}} = {m_5}\left( {\frac{{L_5^2}}{3} + \frac{{{L_5}{L_1}}}{2}} \right)\dot \alpha {\rm{\;}} + {m_5}\frac{{L_5^2}}{3}\dot \beta\)
Question
Q3. En déduire que le moment dynamique galiléen de la tige (5) au point C et en projection sur \({Z_0}\) peut s'écrire sous la forme :
\(\overrightarrow {{\delta _{C,5/0}}} \;\overrightarrow {.{z_0}} = M_{12} \ddot\alpha+M_{22} \ddot\beta\) avec\( {M_{21}}\) et \({M_{22}}\) deux grandeurs à exprimer en fonction des données fournies.
Solution
\(\overrightarrow {{\delta _{C,5/0}}} \;\overrightarrow {.{z_0}} = \left( {\frac{{d\left( {\overrightarrow {{\sigma _{C,5/0}}} } \right)}}{{dt{|_0}}} + \overrightarrow {{V_{C/0}}} \wedge {m_5}\overrightarrow {{V_{G5,5/0}}} } \right)\overrightarrow {.{z_0}} $=$\frac{{d\left( {\overrightarrow {{\sigma _{C,5/0}}} \;\overrightarrow {.{z_0}} } \right)}}{{dt}} + \overrightarrow {{V_{\left( {C5,5/0} \right)}}} \wedge {m_5}\overrightarrow {{V_{\left( {G5,5/0} \right)}}}\)
Or \(\overrightarrow {{\delta _{\left( {C,5/0} \right)}}} \cdot \overrightarrow {{z_0}} = \frac{{d\left( {\overrightarrow {{\sigma _{\left( {C,5/0} \right)}}} \cdot \overrightarrow {{z_0}} } \right)}}{{dt}} + \left( {{L_1}\dot \alpha \overrightarrow {{y_1}} \wedge {m_5} \cdot \left( {{L_1}\dot \alpha \overrightarrow {{y_1}} + \frac{{{L_5}}}{2}\left( {\dot \alpha + \dot \beta } \right)\overrightarrow {{y_5}} } \right)} \right) \cdot \overrightarrow {{z_0}}\).
.
Or \(\frac{{d\left( {\overrightarrow {{\sigma _{\left( {C,5/0} \right)}}} \cdot \overrightarrow {{z_0}} } \right)}}{{dt}} = {m_5}\frac{d}{{dt}}\left( {\frac{{{L_5}{L_1}}}{2}\dot \alpha {\rm{\;cos\;}}\beta + \frac{{L_5^2}}{3}\left( {\dot \alpha + \dot \beta } \right)} \right)\)
Soit \( \frac{{d\left( {\overrightarrow {{\sigma _{\left( {C,5/0} \right)}}} \cdot \overrightarrow {{z_0}} } \right)}}{{dt}} = {m_5}\left( {\frac{{{L_5}{L_1}}}{2}(\ddot \alpha {\rm{\;cos\;}}\beta -\dot \alpha\dot \beta {\rm{\;sin\;}}\beta)+ \frac{{L_5^2}}{3}\left( {\ddot \alpha + \ddot \beta } \right)} \right)\)
Et \(\left( {{L_1}\dot \alpha \overrightarrow {{y_1}} \wedge {m_5} \cdot \left( {{L_1}\dot \alpha \overrightarrow {{y_1}} + \frac{{{L_5}}}{2}\left( {\dot \alpha + \dot \beta } \right)\overrightarrow {{y_5}} } \right)} \right) \cdot \overrightarrow {{z_0}} = {m_5}\frac{{{L_1}{L_5}}}{2}\dot \alpha \left( {\dot \alpha + \dot \beta } \right){\rm{sin\;}}\beta\).
Soit alors \(\overrightarrow {{\delta _{\left( {C,5/0} \right)}}} \cdot \overrightarrow {{z_0}} =m_5\left(\frac{{{L_1}{L_5}}}{2}\left(\ddot \alpha {\rm{cos\;}}\beta+\dot \alpha^2 {\rm{sin\;}}\beta\right)+ \frac{{L_5^2}}{3}\left( {\ddot \alpha + \ddot \beta } \right)\right)\)
Avec les hypothèses sur les petits angles : \(\overrightarrow {{\delta _{\left( {C,5/0} \right)}}} \cdot \overrightarrow {{z_0}} =m_5\left(\frac{{{L_1}{L_5}}}{2}\left(\ddot \alpha+\dot \alpha^2 \beta\right)+ \frac{{L_5^2}}{3}\left( {\ddot \alpha + \ddot \beta } \right)\right)\)
et en négligeant les termes d'ordre>=2 : \(\overrightarrow {{\delta _{\left( {C,5/0} \right)}}} \cdot \overrightarrow {{z_0}} =m_5\left(\frac{{{L_1}{L_5}}}{2}\left(\ddot \alpha+\ddot \beta\right)+ \frac{{L_5^2}}{3} {\ddot \beta } \right)=m_5\left(\ddot \alpha\left(\frac{{{L_1}{L_5}}}{2}+\frac{{L_5^2}}{3}\right)+ \frac{{L_5^2}}{3} {\ddot \beta } \right)\)
donc \({M_{21}} = {m_5}\left( {\frac{{{L_5}{L_1}}}{2} + \frac{{L_5^2}}{3}} \right)\) et \({M_{22}} = {m_5}\frac{{L_5^2}}{3}\)