Mesure d'un moment d'inertie
Dispositif de mesure d'un moment d'inertie
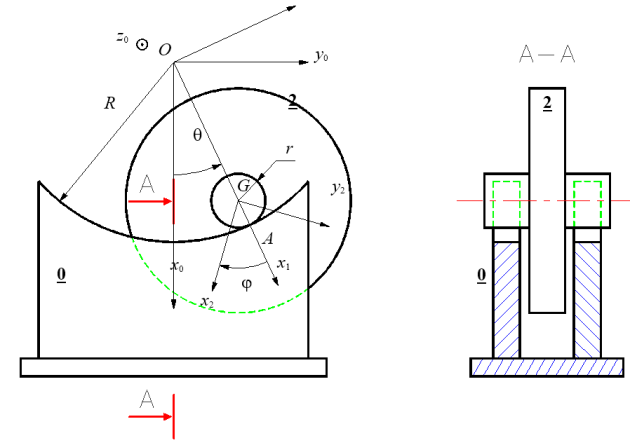
Le mécanisme étudié est conçu pour déterminer le moment d'inertie d'un solide 2 par rapport à son axe de révolution à partir de la mesure de la période de son oscillation sur deux portées cylindriques de rayon R d'un bâti 0.
Le repère orthonormé R0 \((O{\rm{ ; }}{\vec x_0},{\vec y_0},{\vec z_0})\),lié au bâti 0, est considéré comme galiléen.
La direction \(\vec x_0\) est verticale descendante. Le champ de pesanteur est défini par : \(\vec g = g\;{\vec x_0}\)
L'axe \(\left( {O,{{\vec z}_0}} \right)\) coïncide avec l'axe des portées cylindriques du bâti 0.
Le solide 2, de masse m et de centre d'inertie G, possède deux tourillons de rayon r \((r \ll R)\) qui roulent sans glisser (en A) sur les portées cylindriques du bâti 0.
On note f le coefficient de frottement de glissement entre 2 et 0. La résistance au roulement est négligée.
Un repère intermédiaire R1 \((O{\rm{ ; }}{\vec x_1},{\vec y_1},{\vec z_1} = {\vec z_0})\) permet d'exprimer les coordonnées cylindriques du point G : \(\overrightarrow {OG} = \left( {R - r} \right)\;{\vec x_1}\)
Et : \(\theta = \left( {{{\vec x}_0},{{\vec x}_1}} \right)\)
Au solide 2 est associé le repère R2 \((G{\rm{ ; }}{\vec x_2},{\vec y_2},{\vec z_2} = {\vec z_0})\). On pose : \(\varphi = \left( {{{\vec x}_1},{{\vec x}_2}} \right)\)
Question
Q1. Quelle est la relation qui lie les paramètres \(\theta\) et \(\varphi\) ?
Solution
Traduisons le non-glissement en A :
\(\overrightarrow {{V_{A,2/0}}} = \overrightarrow 0 = \overrightarrow {{V_{G,2/0}}} + \overrightarrow {{\Omega _{2/0}}} \wedge \overrightarrow {GA} \) or on peut calculer \(\overrightarrow {{V_{G,2/0}}}\) en passant par O, en effet G reste sur \(O,\overrightarrow {{x_1}}\) on écrira alors : \(\overrightarrow {{V_{G,2/0}}}= \overrightarrow {{\Omega _{1/0}}} \wedge \overrightarrow {OG}\) et donc \( \overrightarrow {{V_{A,2/0}}} = \overrightarrow 0 =\overrightarrow {{\Omega _{1/0}}} \wedge \overrightarrow {OG} + \overrightarrow {{\Omega _{2/0}}} \wedge \overrightarrow {GA}\)
\(\begin{array}{l}\overrightarrow {{V_{A,2/0}}} = \dot \theta \overrightarrow {{z_0}} \wedge (R - r)\overrightarrow {{x_1}} + (\dot \theta + \dot \varphi )\overrightarrow {{z_0}} \wedge r\overrightarrow {{x_1}} \\\overrightarrow {{V_{A,2/0}}} = \left[ {\dot \theta (R - r) + (\dot \theta + \dot \varphi )r} \right]\overrightarrow {{y_1}} = \left[ {R\dot \theta +r \dot \varphi} \right]\overrightarrow {{y_1}}\end{array}\)
D'où : \(r\,\dot \varphi = - R\,\dot \theta\)
Question
Q2. Donner la forme de la matrice d'inertie du solide 2 en G dans R2.
Solution
Matrice d'un solide de révolution autour de \(\left( {G,{{\vec z}_0}} \right)\) donc diagonale avec A, B et C et A=B.
Question
Q3. Déterminer l'équation du mouvement de S par rapport à S0 en fonction de \( \theta\).
Solution
Méthode :
On isole S, on écrit le TMD en A sur \(\vec z_0\).
Actions mécaniques
BAME :
\(S_0 \to S\) :
Cylindre plan avec frottement et hypothèse problème plan
\(\left\{ {{T}_{S_0\to S}} \right\}={{\left\{ \begin{matrix} -Y_{S}\overrightarrow{{{y}_{1}}}-X_{S}\overrightarrow{{{x}_{1}}}\\ {\vec{0}} \\ \end{matrix} \right\}}_{A}}\).
Pesanteur sur S :
\(\left\{ {{T}_{pes\to S}} \right\}={{\left\{ \begin{matrix} mg\overrightarrow{{{x}_{0}}}\\ {\vec{0}} \\ \end{matrix} \right\}}_{\forall P \in (G,\overrightarrow{{{x}_{0}}})}}\).
Moment en A sur \(\overrightarrow{{{z}_{0}}}\):
\(\overrightarrow{{{M}_{A,ext \to S}}}=\overrightarrow{{{M}_{A,pes \to S}}}+\overrightarrow{{{M}_{A,S_0 \to S}}}\)
Or \(\overrightarrow{{M}_{A,pes \to S}}=\overrightarrow {AG} \wedge mg\overrightarrow{{{x}_{0}}}=mgr.sin \theta \overrightarrow{z_0}\)
et \(\overrightarrow{{{M}_{A,S_0 \to S}}}=\vec 0\)
Soit \(\overrightarrow{{{M}_{A,ext \to S}}}.\overrightarrow{{{z}_{01}}}=mgr.sin \theta \)
Solution
Grandeurs dynamiques
Moment dynamique en A sur \(\overrightarrow{{{z}_{0}}}\):
Ici le centre de gravité de S est C :
\(\overrightarrow{\delta_{A,S/0}}.\overrightarrow{{{z}_{0}}}=\frac{d}{dt}_{0}(\overrightarrow{\sigma_{A,S/0}}.\overrightarrow{{{z}_{0}}}) +m \overrightarrow {{V_{A/0}}} \wedge \overrightarrow {{V_{G,S/0}}} .\overrightarrow{{{z}_{0}}}=\frac{d}{dt}_{0}(\overrightarrow{\sigma_{A,S/0}}.\overrightarrow{{{z}_{0}}}) \)
Avec \(\overrightarrow{\sigma_{A,S/0}}.\overrightarrow{z_{0}}=\overrightarrow{\sigma_{G,2/0}}.\overrightarrow{z_{0}}+\overrightarrow{AG} \wedge m\overrightarrow {{V_{G,2/0}}}.\overrightarrow{z_{0}}\) or \(\overrightarrow {V_{G,2/0}}= (R-r) \dot \theta\overrightarrow{y_{1}}\)
\(\overrightarrow{\sigma_{A,S/0}}.\overrightarrow{z_{0}}=C(\dot \theta + \dot \varphi )-r\overrightarrow{x_1} \wedge m (R-r) \dot \theta \overrightarrow{y_{1}}.\overrightarrow{z_{0}}=C(\dot \theta + \dot \varphi )-mr(R-r)\dot \theta\)
Donc \(\overrightarrow{\delta_{A,2/0}}.\overrightarrow{z_{0}}=C(\ddot \theta + \ddot \varphi )-mr(R-r)\ddot \theta\)
Soit \(\overrightarrow{\delta_{A,2/0}}.\overrightarrow{z_{0}}=C(\ddot \theta - \frac{R}{r}\ddot \theta )-mr(R-r)\ddot \theta=\ddot \theta[\frac{C }{r}(r-R)-mr(R-r)]= -\ddot \theta(R-r)[\frac{C}{r}+{mr}\)
Solution
Équation du mouvement
\(- \ddot \theta(R-r)[\frac{C}{r}+mr]=mgr.sin \theta\)
Soit donc \( \left( {R - r} \right)\,\left( {\frac{C}{{{r^2}}} + m} \right)\,\ddot \theta +m\,g\,\sin \theta = 0\)
Question
Q4. On suppose que l'angle \(\theta\) reste petit au cours du mouvement. Montrer que le mouvement est périodique et déterminer la période T des oscillations de S. En déduire le moment d'inertie I de S sachant que : T = 5s; a = 12,5 mm; r = 141,1 mm; g = 9,81 m/s²; m = 7217 g; f = 0,15
Solution
On a \( \left( {R - r} \right)\,\left( {\frac{C}{{{r^2}}} + m} \right)\,\ddot \theta +m\,g\, \theta = 0\) soit donc \( \frac{(R - r)}{r^2} (C+mr^2)\ddot \theta +m\,g\, \theta = 0\)
\( \frac{(R - r)(C+mr^2)}{r^2} \ddot \theta +m\,g\, \theta = 0\)
On a alors \(T=\frac{2 \pi}{\omega_0}\) avec \(\omega_0=\sqrt{ \frac{(R - r)(C+mr^2)}{mgr^2} }\)
Question
Q5. Déterminer le coefficient de frottement mini pour qu'il n'y ait pas glissement au cours du mouvement.
Solution
Avec le TRS on a :
Actions mécaniques en résultante :
\(\left\{ {{T}_{S_0\to S}} \right\}={{\left\{ \begin{matrix} -Y_{S}\overrightarrow{{{y}_{1}}}-X_{S}\overrightarrow{{{x}_{1}}}\\ {\vec{0}} \\ \end{matrix} \right\}}_{A}}\).
\(\left\{ {{T}_{pes\to S}} \right\}={{\left\{ \begin{matrix} mg\overrightarrow{{{x}_{0}}}\\ {\vec{0}} \\ \end{matrix} \right\}}_{\forall P \in (G,\overrightarrow{{{x}_{0}}})}}\).
- sur \(\overrightarrow{{{x}_{1}}}\) :\(-X_S+mg cos\theta\)
- sur \(\overrightarrow{{{y}_{1}}} \): \(-Y_S-mg sin\theta\)
Résultante dynamique :
\(m\overrightarrow {{a_{G,2/0}}}.=m(R-r) (\ddot \theta \overrightarrow{y_{1}}-\dot \theta^2\overrightarrow{x_{1}})\)
Bilan :
\(Y_S=m(R-r) \ddot \theta+mg sin\theta\)
\(X_S=mg cos\theta-m(R-r) \dot \theta^2\)
Soit \(f > \left| {\frac{{{Y_S}}}{{{X_S}}}} \right| = \left| {\frac{{mg\sin \theta + m(R - r)\ddot \theta }}{{mg\cos \theta - m(R - r){{\dot \theta }^2}}}} \right|\)