Robot manipulateur à axes parallèles
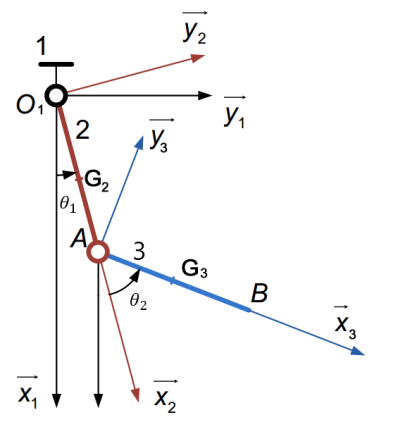
Le robot manipulateur représenté ci-dessous possède deux degrés de liberté: une rotation de l'avant-bras (2) par rapport au socle (1) au niveau de la liaison pivot située en \({O}_{1}\): la rotation est paramétrée par l'angle \({\mathrm{\theta }}_{1}\). Un moteur électrique \({M}_{1}\) solidaire de (1) anime cette rotation,
une rotation du bras (3) par rapport à l'avant-bras (2) au niveau de la liaison pivot située en A : la rotation est paramétrée par l'angle \({\mathrm{\theta }}_{2}\). Un moteur électrique \({M}_{2}\) solidaire de (2) anime cette rotation.
Le mécanisme évolue dans le plan \(\left({O}_{1}\mathrm{,}{\vec{x}}_{1}\mathrm{,}{\vec{y}}_{1}\right)\) horizontal (le poids est sur \(\vec{{z}_{1}}\)). Les liaisons sont parfaites. Le but de cet exercice est de déterminer le couple qu'il est nécessaire d'exercer au niveau de l'articulation en A afin de contrôler le mouvement de (3).
Le bras (3) a une masse notée \({m}_{3}\) et \(\begin{array}{c}\\\\I\left(A\mathrm{,}3\right)={\left\lbrack \begin{array}{ccc}A_3&0&0 \\0& {B}_{3}& 0\\0 &0& {C}_{3}\end{array}\right\rbrack }_{}\end{array}_{{A}_{3},(B_3)}\)
\({O}_{1}A={l}_{2}\)\(\mathit{AB}={l}_{3}\)
\({O}_{1}{G}_{2}=a\)
\({\mathit{AG}}_{3}=b\)
Question
Q1. Isoler 3 faire le BAME, on donnera l'expression du torseur \(\left\lbrace {T}_{2\rightarrow 3}\right\rbrace \) en A dans la base \({R}_{2}\).
Solution
On isole 3.
BAME :
\(\left\lbrace {T}_{2\rightarrow 3}\right\rbrace ={\left\lbrace \begin{array}{cc}{X}_{A} &{L}_{A}\\{Y}_{A}& {M}_{A}\\{Z}_{A}& 0\end{array}\right\rbrace }_{A,{R}_{3}}\) , \(\begin{array}{c}\left\lbrace {T}_{\text{pesanteur}\rightarrow 3}\right\rbrace ={\left\lbrace \begin{array}{cc}0& 0\\0& 0\\-{m}_{3}g& 0\end{array}\right\rbrace }_{G_3,R_3}\end{array}\) et \(\begin{array}{c} \left\lbrace {T}_{\text{moteur2}\rightarrow 3}\right\rbrace ={\left\lbrace \begin{array}{cc}0& 0\\0& 0\\0 &{C}_{2}\end{array}\right\rbrace }_{A,R_3}\end{array}\)
Question
Q2. Appliquer le PFD sous forme torsorielle (sans calcul) appliqué à (3) et en déduire l'équation scalaire du PFD permettant d'obtenir l'équation du mouvement reliant \({\mathrm{\theta }}_{2}\) aux paramètres géométriques et de masse du mécanisme.
Solution
1 est Galiléen, \(\left\lbrace {D}_{3/1}\right\rbrace =\left\lbrace {T}_{2\rightarrow 3}\right\rbrace +\left\lbrace {T}_{\text{pesanteur}\rightarrow 3}\right\rbrace +\left\lbrace {T}_{\text{moteur2}\rightarrow 3}\right\rbrace \)
La seule équation ne faisant pas intervenir d'inconnue de liaison est l'équation de moment sur l'axe \(\left(A,\vec{{z}_{1}}\right)\).
Question
Q3. Déterminer les expressions des éléments des torseurs cinétiques et dynamiques nécessaires pour déterminer l'équation différentielle du mouvement.
Solution
\(\begin{array}{c}\overrightarrow{{\mathrm{\sigma }}\left(A\mathrm{,3}/1\right)}=I\left(A,{R}_{3}\right)\vec{\mathrm{\Omega }}\left(3/1\right)+{m}_{3}\vec{{\mathit{AG}}_{3}}\mathrm{\wedge }\vec{V}\left(A\mathrm{,3}/1\right)\hfill\\ \overrightarrow{{\mathrm{\sigma }}\left(A\mathrm{,3}/1\right)}={C}_{3}\left(\dot{{\mathrm{\theta}}_{1}}+\dot{{\mathrm{\theta}}_{2}}\right)\vec{{z}_{1}}+{m}_{3}b\vec{{x}_{3}}\mathrm{\wedge}{l}_{2}\dot{{\mathrm{\theta }}_{1}}\vec{{y}_{2}}=\left({C}_{3}\left(\dot{{\mathrm{\theta }}_{1}}+\dot{{\mathrm{\theta}}_{2}}\right)+{m}_{3}b{l}_{2}\cos{\mathrm{\theta}}_{2}\dot{{\mathrm{\theta }}_{1}}\right)\vec{{z}_{1}}\hfill \end{array}\)
\(\overrightarrow {\delta {}_{A,{\rm{3}}/1}} = \frac{{{\rm{d}}\overrightarrow {{\sigma _{A,{\rm{3}}/1}}} }}{{{{\left. {{\rm{dt}}} \right|}_0}}} + {m_3}\overrightarrow {{V_{A/1}}} \wedge \overrightarrow {{V_{{G_3},{\rm{3}}/1}}} \) ici le point A choisit est le centre de la pivot entre 2 et 3 soit :\( \overrightarrow {{V_{A/1}}}=\overrightarrow {{V_{A,2/1}}} \)
\(\begin{array}{c}\overrightarrow{{\mathrm{\delta }}\left(A\mathrm{,3}/1\right)}=\left({C}_{3}\left(\ddot{{\mathrm{\theta }}_{1}}+\ddot{{\mathrm{\theta }}_{2}}\right)+{m}_{3}b{l}_{2}\cos {\mathrm{\theta }}_{2}\ddot{{\mathrm{\theta }}_{1}}-{m}_{3}b{l}_{2}\sin \left({\mathrm{\theta }}_{2}\right)\dot{{\mathrm{\theta }}_{2}}\dot{{\mathrm{\theta }}_{1}}\right)\vec{{z}_{1}}+{m}_{3}{l}_{2}\dot{{\mathrm{\theta }}_{1}}\vec{{y}_{2}}\mathrm{\wedge }\left({l}_{2}\dot{{\mathrm{\theta }}_{1}}\vec{{y}_{2}}+b\left(\dot{{\mathrm{\theta }}_{1}}+\dot{{\mathrm{\theta }}_{2}}\right)\vec{{y}_{3}}\right)\hfill \\\overrightarrow{{\mathrm{\delta }}\left(A\mathrm{,3}/1\right)}=\left({C}_{3}\left(\ddot{{\mathrm{\theta }}_{1}}+\ddot{{\mathrm{\theta }}_{2}}\right)+{m}_{3}b{l}_{2}\cos {\mathrm{\theta }}_{2}\ddot{{\mathrm{\theta }}_{1}}-{m}_{3}b{l}_{2}\sin \left({\mathrm{\theta }}_{2}\right)\dot{{\mathrm{\theta }}_{2}}\dot{{\mathrm{\theta }}_{1}}\right)\vec{{z}_{1}}+{m}_{3}{l}_{2}b\dot{{\mathrm{\theta }}_{1}}\left(\dot{{\mathrm{\theta }}_{1}}+\dot{{\mathrm{\theta }}_{2}}\right)\sin \left({\mathrm{\theta }}_{2}\right)\vec{{z}_{1}}\hfill \\\overrightarrow{{\mathrm{\delta }}\left(A\mathrm{,3}/1\right)}=\left({C}_{3}\left(\ddot{{\mathrm{\theta }}_{1}}+\ddot{{\mathrm{\theta }}_{2}}\right)+{m}_{3}b{l}_{2}\cos {\mathrm{\theta }}_{2}\ddot{{\mathrm{\theta }}_{1}}+{m}_{3}b{l}_{2}\sin \left({\mathrm{\theta }}_{2}\right)\dot{{\mathrm{\theta }}_{1}^{2}}\right)\vec{{z}_{1}}\hfill \end{array}\)
Question
Q4. Dans l'hypothèse où le moteur \({M}_{2}\) n'exerce aucun couple sur (3), déterminer l'équation différentielle du mouvement de (3) par rapport à (2).
Solution
En appliquant le théorème du moment dynamique sur l'axe \(\left(A,\vec{{z}_{1}}\right)\), on obtient
\({C}_{3}\left(\ddot{{\mathrm{\theta }}_{1}}+\ddot{{\mathrm{\theta }}_{2}}\right)+{m}_{3}b{l}_{2}\cos {\mathrm{\theta }}_{2}\ddot{{\mathrm{\theta }}_{1}}+{m}_{3}b{l}_{2}\sin \left({\mathrm{\theta }}_{2}\right)\dot{{\mathrm{\theta }}_{1}^{2}}=0\) (le poids étant dirigé sur \(\vec{{z}_{1}}\) il ne pourra pas créer de moment sur cet axe).
Question
Q5. A l'instant initial \(\dot{{\mathrm{\theta }}_{1}}\), \({\mathrm{\theta }}_{1}\) sont nuls, \({\mathrm{\theta }}_{2}\) quelconque. L'avant-bras (2) subit une accélération angulaire \(\ddot{{\mathrm{\theta }}_{1}}\) positive. Quel est le mouvement de (3) par rapport à (2) . (réponse qualitative sachant que \({C}_{3}\approx {m}_{3}\frac{{l}_{3}^{2}}{3}\), \({l}_{3}\approx {l}_{2}\) et \(b\approx \frac{{l}_{3}}{2}\)).
Solution
On simplifie l'équation différentielle précédente pour les hypothèses énoncées :
\({m}_{3}\frac{{l}_{3}^{2}}{3}\left(\ddot{{\mathrm{\theta }}_{1}}+\ddot{{\mathrm{\theta }}_{2}}\right)+{m}_{3}\frac{{l}_{3}^{2}}{2}\cos {\mathrm{\theta }}_{2}\ddot{{\mathrm{\theta }}_{1}}=0\)donc \(\left(\ddot{{\mathrm{\theta }}_{1}}+\ddot{{\mathrm{\theta }}_{2}}\right)+\frac{3}{2}\cos {\mathrm{\theta }}_{2}\ddot{{\mathrm{\theta }}_{1}}=0\)
et \(\ddot{{\mathrm{\theta }}_{2}}=-\left(1+\frac{3}{2}\cos {\mathrm{\theta }}_{2}\right)\ddot{{\mathrm{\theta }}_{1}}\)
En fonction de la valeur initiale de \({\mathrm{\theta }}_{2}\) :
la barre 2 partira dans le sens horaire si \(\cos {\mathrm{\theta }}_{2}> -\frac{2}{3}\)
la barre 2 partira dans le sens trigonométrique si \(\cos {\mathrm{\theta }}_{2}< -\frac{2}{3}\)