Véhicule Eco Marathon Shell
Présentation
L'écomarathon SHELL est une compétition relative à la consommation énergétique des moyens de propulsion automobile. Les concurrents doivent concevoir et piloter leur véhicule sur une distance fixée avec une vitesse minimale imposée.
Les candidats sont ensuite classés en fonction de la consommation de leur véhicule, exprimée en kilomètre par litre de carburant. L'étude sur ce sujet, issue d'un projet élaboré par l'équipe T.I.M. de l'INSA Toulouse, a pour objet de quantifier les effets résistants et dissipatifs que sont la résistance au roulement et les actions aérodynamiques sur les performances de leur véhicule. Les effets inertiels étant plutôt quantifiés numériquement au niveau de la conception assistée par ordinateur du véhicule.

Détermination expérimentale du coefficient de résistance au roulement
Le principe est présenté sur la figure ci-contre. On place 2 roues lestées sur un dispositif inclinable. On considère ensuite que l'angle d'inclinaison minimum de la pente, où il y a début du mouvement des roues, est représentatif de la résistance au roulement.
L'ensemble des 2 roues lestées peut être assimilé à un solide 1 représenté sur la figure 1, de masse m, de rayon R et de centre de masse G. L'accélération de la pesanteur est tel que \( \vec g = - g\overrightarrow {{z_0}}\) .
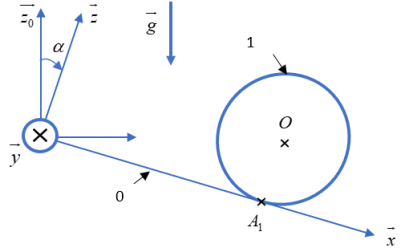
L'action de contact entre l'ensemble des roues 1 et le plan 0, incliné d'un angle \( \alpha\) par rapport à l'horizontale, est modélisé comme un contact ponctuel avec frottement où l'on tient compte de la résistance au roulement.
Cette action de contact peut s'écrire : \( \left\{ {{F_{0 \to 1}}} \right\} = {\left\{ {\begin{array}{*{20}{l}}{ - {T_{01}}.\vec x + {N_{01}}.\vec z}\\{ - {C_r}.\vec y}\end{array}} \right\}_{{A_1}}}\) où \({C_r}\) représente le couple de résistance au roulement qui s'oppose au roulement tel que: \( \left| {{C_r}\left| { = r.} \right|{N_{01}}} \right|\) à la limite de l'équilibre et\( \left| {{C_r}} \right|\left\langle {r.} \right|{N_{01}}|\) à l'équilibre.
Question
Q1. Écrire le principe fondamental de la statique appliqué au solide 1 réduit au point G en projection sur la base \(\left( {\vec x,\vec y,\vec z} \right)\).
Solution
Théorème de la résultante statique :
sur \(\vec x\) : \(- {T_{01}} - mg.sin\alpha = 0\) sur \(\vec z\) :\( {N_{01}} - mg\cos \alpha = 0\)
Théorème du moment statique en O projection sur \(\vec y:\;\;R.{T_{01}} - {C_r} = 0\)
Question
Q2. Déterminer l'expression analytique de l'angle \({\alpha _{{\rm{lim}}}}\) à la limite de l'équilibre quand il y a début du roulement du solide sur le plan 0.
Solution
A la limite du roulement on a \( {C_r} = r.{N_{01}}\) soit \(R.{T_{01}} - r.{N_{01}} = 0\) donc \(R.m.g.\sin {\alpha _{{\rm{lim}}}} - r.m.g.\cos {\alpha _{{\rm{lim}}}} = 0 \Rightarrow tan{\alpha _{{\rm{lim}}}} = \frac{r}{R}\)
Pour une masse du solide 1 m=50kg et pour un rayon R=0,25m le roulement se produit à partir d'un angle \({\alpha _{{\rm{lim}}}}\) tel que \(tan{\alpha _{{\rm{lim}}}}=0.008\) .
Question
Q3. Déterminer le coefficient de résistance au roulement r.
Solution
On incline le plan jusqu'à obtenir roulement de la roue, on obtient expérimentalement\( {\alpha _{{\rm{lim}}}}\).
Pour \(tan{\alpha _{{\rm{lim}}}} = 0,008\) et R = 0,25m on a \(r = R.{\rm{\;tan\;}}{\alpha _{{\rm{lim}}}} = 0,25 \times 0,008 = 0,002m.\)
Question
Q4. Au début du roulement, montrer qu'il ne peut pas y avoir glissement en \({A_1}\) si le coefficient de frottement au contact vaut f = 0,5.
Solution
Loi de Coulomb en phase d'adhérence on a \({T_{01}} \le f.{N_{01}}\). Il faut donc déterminer le rapport \(\frac{{{T_{01}}}}{{{N_{01}}}}\) : On a \({T_{01}} = m.g.\sin \alpha = 0\) et \({N_{01}} = m.g.\cos \alpha\)
\(\frac{{{T_{01}}}}{{{N_{01}}}} = \frac{{m. \cdot g. \cdot {\rm{\;sin\;}}\alpha }}{{mg{\rm{\;cos\;}}\alpha }} = {\rm{\;tan\;}}\alpha\) . Pour \(\alpha = {\alpha _{{\rm{lim}}}}\) on a donc \(\frac{{{T_{01}}}}{{{N_{01}}}} = 0,008 < 0,5\) a il y a donc roulement mais non glissement de la roue.
Modélisation du véhicule
L'objectif est d'établir un modèle analytique du véhicule, lors d'une phase de roulement sans glissement sur une ligne droite inclinée d'un angle \(\alpha\) , en l'absence de vent. En adoptant des conditions particulières d'essai, il sera possible d'identifier, précisément grâce à ce modèle, les actions aérodynamiques.
Le modèle est donné
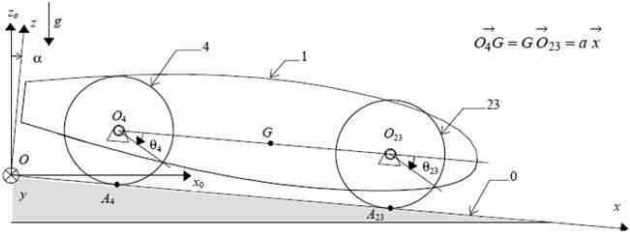
On considère que le véhicule se déplace sur une pente inclinée d'un angle \(\alpha\) par rapport à l'horizontale. Le véhicule est constitué :
• d'un châssis avec son pilote : solide 1de centre d'inertie G, de masse M en translation par rapport au repère galiléen R avec \(\overrightarrow {OG} = x.\vec x + R.\vec z\)
• de deux roues avant : solide 23 de centre d'inertie \( {O_{23}}\), de masse 2 m, de rayon R, dont le moment d'inertie par rapport à l'axe \(\left( {{O_{23}},\vec y} \right)\) sera noté 2 I. Le solide 23 est en liaison pivot sans frottement par rapport au châssis d'axe \(\left( {{O_{23}},\vec y} \right)\) caractérisé par le paramètre \({\theta _{23}}\).
• d'une roue arrière motrice : solide 4 de centre d'inertie \({O_4}\), de masse m, de rayon R, dont le moment d'inertie par rapport à l'axe \( \left( {{O_4},\vec y} \right)\) sera noté I. Le solide 4 est en liaison pivot sans frottement par rapport au châssis d'axe \( \left( {{O_4},\vec y} \right)\) caractérisé par le paramètre \({\theta _4}\).
• un moteur d'entraînement du véhicule dont le corps est solidaire du châssis 1 exerce sur la roue 4 un couple moteur noté \({C_m}.\vec y\)
Les roues sont en contact ponctuel avec frottement avec le sol 0. Afin de tenir compte de la résistance au roulement du pneu sur le sol, les actions de contact peuvent être modélisées en dynamique par : \(\left\{ {{F_{0 \to i}}} \right\} = {\left\{ {\begin{array}{*{20}{l}}{ - {T_{0i}}.\vec x + {N_{0i}}.\vec z}\\{ - {N_{0i}}.r.\vec y}\end{array}} \right\}_{{A_i}}}\) avec i = 4 ou 23.
L'ensemble du véhicule dont la carrosserie est soumis lors de son mouvement à un effort de traînée aérodynamique qui peut être modélisé par le torseur\( {\left\{ {\begin{array}{*{20}{l}}{ - \frac{1}{2}\rho .S{C_x}.{{\dot x}^2}.\vec x}\\{\vec 0}\end{array}} \right\}_{{O_{23}}}}\)
avec \(\rho\) : masse volumique du véhicule, S : surface alaire, Cx : coefficient de traînée du véhicule, \(\dot x\) : vitesse relative du véhicule par rapport à l'air ambiant.
Question
Q5. Écrire les équations scalaires découlant des conditions de Roulement Sans Glissement (RSG) au point \({A_{23}}\) et \({A_4}\).
Solution
\(\overrightarrow {{V_{{A_{23'}}23/0}}} = \vec 0 \Rightarrow \overrightarrow {{V_{{A_{23'}}23/1}}} + \overrightarrow {{V_{{A_{23'}}1/0}}} = \vec 0 \Rightarrow - R{\theta _{23}} + x = 0\)
\(\overrightarrow {{V_{{A_{4'}}4/0}}} = \vec 0 \Rightarrow \overrightarrow {{V_{{A_{4'}}4/1}}} + \overrightarrow {{V_{{A_{4'}}1/0}}} = \vec 0 \Rightarrow - R{\theta _4} + x = 0\)
Question
Q6. En isolant l'ensemble \(E = 1 + 23 + 4\), écrire le théorème de la résultante dynamique en projection sur \(\vec x\) et \(\vec z\).
Solution
Théorème de Ia résultante dynamique : \(\overrightarrow {{R_{\bar E \to E}}} = \overrightarrow {{R_{d\;E/R}}}\)
Avec \(\overrightarrow {{R_{d\;E/R}}} = \overrightarrow {{R_{d\;E/0}}} = \overrightarrow {{R_{d1/0}}} + \overrightarrow {{R_{d23/0}}} + \overrightarrow {{R_{d4/0}}}\) \(\;{O_{23}}\) est cdg de 23 et \( {O_4}\) est cdg de 4
On a alors :
\(\overrightarrow {{R_{d\;1/R}}}=M.\overrightarrow {{a_{{G_{1,}}1/0}}} =M.\ddot x .\vec x\)
\(\overrightarrow {{R_{d\;23/R}}}=M.\overrightarrow {{a_{{O_{23,}}23/0}}} =2.m.\ddot x .\vec x\)
\(\overrightarrow {{R_{d\;4/R}}}=M.\overrightarrow {{a_{{O_{4,}}4/0}}} =m.\ddot x .\vec x\)
Donc on a :
\(\overrightarrow {{R_{d\;E/R}}}=(3m+M).\ddot x .\vec x\)
En projection :
sur \(\vec x\) : \(- {T_{023}} - {T_{04}} + \left( {M + 3.m} \right).g.\sin \alpha - \frac{1}{2}\rho .S{C_x}.{\dot x^2}=(3m+M).\ddot x \)
sur \(\vec z\) : \({N_{023}} + {N_{04}} - \left( {M + 3.m} \right).g.\cos \alpha = 0\)
Question
Q7. Pour chacune des roues 23 et 4, écrire les 2 équations scalaires correspondant au théorème du moment dynamique respectivement en \({O_{23}}\) et \({O_4}\) en projection sur \(\vec y\).
Solution
On isole l'ensemble roue 23, on effectue le BAME et on applique le PFD sur 23 en \(O_{23}\)centre de gravité de 23 ∶
Théorème du moment dynamique en\( {O_{23}}\) en projection sur\( \vec y\;:\overrightarrow {{\delta _{{0_{23'}}23/0}}} .\vec y = \overrightarrow {{M_{{O_{23}}\left( {\overline {23} \to 23} \right)}}} .\vec y\)
Avec \(\overrightarrow {{\delta _{{0_{23'}}23/0}}} .\vec y = \frac{d}{{dt}}{\left( {\overrightarrow {{\sigma _{{0_{23'}}23/0}}} .\vec y} \right)_{}} \) et \( \overrightarrow {{\sigma _{{0_{23'}}23/0}}} = {I_{{O_{23}}}}\left( {23} \right).\overrightarrow {{\Omega _{23/0}}}\) soit \(\Rightarrow \;\overrightarrow {{\delta _{{0_{23'}}23/0}}} .\vec y = 2.I.{\ddot \theta _{23}}\).
On isole la roue 4, on effectue le BAME et on applique le PFD sur 4 en \(O_4\) centre de gravité de 4 :
Théorème du moment dynamique en \({O_4}\) en projection sur\( \overrightarrow {y\;} : \overrightarrow {{\delta _{{0_{4'}}4/0}}} .\vec y = \overrightarrow {{M_{{O_4}\left( {\bar 4 \to 4} \right)}}} .\vec y\) avec\( \overrightarrow {{\delta _{{0_{4'}}4/0}}} .\vec y = \frac{d}{{dt}}\left( {\overrightarrow {{\sigma _{{0_{4'}}4/0}}} .\vec y} \right)\; \Rightarrow \overrightarrow {{\delta _{{0_{4'}}4/0}}} .\vec y = I.\ddot \theta_4 \;\)
Question
Q8. Montrer à partir des équations scalaires obtenues précédemment que le couple moteur \({C_m}\) vaut :
\({C_m} = \left( {M + 3.m} \right).g.{\rm{\;cos\;}}\alpha .r + \left[ {\frac{{3.I}}{R} + R.\left( {M + 3.m} \right)} \right].\ddot x - R.\left( {M + 3.m} \right).g.{\rm{\;sin\;}}\alpha + \frac{1}{2}R.\rho .S.{C_x}.{\dot x^2}\)
Solution
Rappel des équations :
\(- {T_{023}} - {T_{04}} + \left( {M + 3.m} \right).g.{\rm{\;sin\;}}\alpha - \frac{1}{2}\rho .S.{C_x}.{\dot x^2} = \left( {M + 3.m} \right).\ddot x\)
\({N_{023}} + {N_{04}} - \left( {M + 3.m} \right).g.{\rm{\;cos\;}}\alpha = 0\)
\(2.I.{\ddot \theta _{23}} = - {N_{023}}.r + {T_{023}}.R$ $I.{\ddot \theta _4} = - {N_{04}}.r + {T_{04}}.R + {C_m}\)
\(- R.{\dot \theta _{23}} + \dot x = 0\) et \( - R.{\dot \theta _4} + \dot x = 0\)
Calculons :
\(\left\{ {\begin{array}{*{20}{c}}{{C_m} = {N_{04}}.r - {T_{04}}.R + I.{{\ddot \theta }_4}}\\{{N_{04}} = \left( {M + 3.m} \right).g.{\rm{\;cos\;}}\alpha - {N_{023}}}\end{array}} \right\}\)
\(\left\{ {\begin{array}{*{20}{c}}{{C_m} = { \left( {M + 3.m} \right).g.{\rm{\;cos\;}}\alpha - {N_{023}}}.r - {T_{04}}.R + I.{{\ddot \theta }_4}}\\{{N_{04}} = 2.I.{{\ddot \theta }_{23}} - {T_{023}}.R = -{N_{023}}.r }\end{array}} \right\}\)
\(\left\{ {\begin{array}{*{20}{c}}{{C_m} = \left( {M + 3.m} \right).g.{\rm{\;cos\;}}\alpha .r + 2.I.{{\ddot \theta }_{23}} - {T_{023}}.R - {T_{04}}.R + I.{{\ddot \theta }_4}}\\{ - {T_{023}} - {T_{04}} = \left( {M + 3.m} \right).\ddot x - \left( {M + 3.m} \right).g.{\rm{\;sin\;}}\alpha + \frac{1}{2}\rho .S.{C_x}.{{\dot x}^2}}\end{array}} \right\}\)
\({C_m} = {M + 3.m} .g.{\rm{\;cos\;}}\alpha .r + 2.I.{\ddot \theta _{23}} + I.{\ddot \theta _4} + R.[ { {M + 3.m} .\ddot x -{M + 3.m} .g.{\rm{\;sin\;}}\alpha + \frac{1}{2}\rho .S.{C_x}.{{\dot x}^2}}]\)
or on a \( {\dot \theta _{23}} = \frac{{\dot x}}{R} \Rightarrow {\ddot \theta _{23}} = \frac{{\ddot x}}{R}\) et \({\dot \theta _4} = \frac{{\dot x}}{R} \Rightarrow {\ddot \theta _4} = \frac{{\ddot x}}{R}\)
\(\Rightarrow {C_m} = \left( {M + 3.m} \right).g.\cos \alpha .r + 2.I.\frac{{\ddot x}}{R} + I.\frac{{\ddot x}}{R} + R.\left( {M + 3.m} \right).\ddot x - R.\left( {M + 3.m} \right).g.\sin \alpha + \frac{1}{2}R.\rho .S.{C_x}.{\dot x^2}\)
\(\Rightarrow {C_m} = \left( {M + 3.m} \right).g.{\rm{\;cos\;}}\alpha .r + \left[ {\frac{{3.I}}{R} + R.\left( {M + 3.m} \right)} \right].\ddot x - R.\left( {M + 3.m} \right).g.{\rm{\;sin\;}}\alpha + \frac{1}{2}R.\rho .S.{C_x}.{\dot x^2}\)
Question
Q9. Identifier dans l'expression de \({C_m}\) les différentes actions qui ont tendance à affecter l'avancement du véhicule.
Solution
D'après l'équation scalaire obtenue question précédente le couple moteur peut se décomposer comme étant \(C_m\)= couple pour vaincre la résistance au roulement +couple pour vaincre les effets inertiels du véhicule+couple lié au binôme poids/pente +couple pour vaincre l'action du vent sur le véhicule.
Question
Q10. Déterminer l'expression du couple moteur \({C_m}\) quand le véhicule a une vitesse constante V sur une piste horizontale.
Solution
A vitesse constante sur une piste horizontale on obtient: \({C_m} = \left( {M + 3.m} \right).g.r + \frac{1}{2}R.\rho .S.{C_x}.{\dot x^2}\)
On réalise un essai du véhicule sur terrain horizontal, le moteur du véhicule délivrant un couple \({C_m}\) constant.
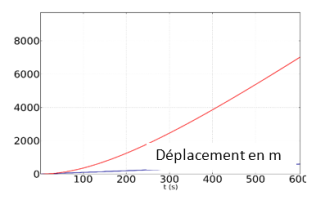
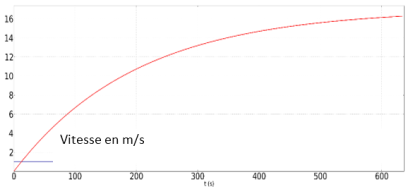
L'acquisition des paramètres vitesse véhicule et distance parcourue sont visualisés par les graphes ci-contre.
Les données véhicules sont : \(M = 70kg,m = 1kg,r = {2.10^{ - 3}}m, R = 0,25m\; et {C_m} = 3,245m.N\)
Question
Q11. Déterminer dans les conditions d'essais le produit\( \frac{1}{2}\rho .S.{C_x}\) caractérisant les effets aérodynamiques sur le véhicule. On précisera les unités.
Solution
Pour t = 500s on est à vitesse constante \(\dot x = 16m/s \Rightarrow \frac{1}{2}\rho .S.{C_x} = \frac{{{C_m} - \left( {M + 3.m} \right).g.r}}{{R.{{\dot x}^2}}}\)
Question
Q12. Évaluer la pente maximum que peut monter ce véhicule à vitesse stabilisée de 5 km/h (on négligera le couple de résistance au roulement).
Solution
A vitesse constante de 5km/h = 1,39m/s et en négligeant la résistance au roulement, on obtient
l'expression de l'angle \(\alpha \) :\( {\rm{\;sin\;}}\alpha = \frac{{{C_m} - \frac{1}{2}R.\rho .S.{C_x}.{{\dot x}^2}}}{{ - R.\left( {M + 3.m} \right).g}}\)
A.N. : \(\alpha = {\rm{\;arcsin\;}}\frac{{3,245 - \frac{1}{2}0,25 \times 0,028 \times {{1,39}^2}}}{{ - 0,25.\left( {70 + 3 \times 1} \right).10}} = - {1^o}\).
Ce qui correspond, compte tenu du paramétrage, à une pente à gravir de 1.