Boitier commande raboteuse
Présentation
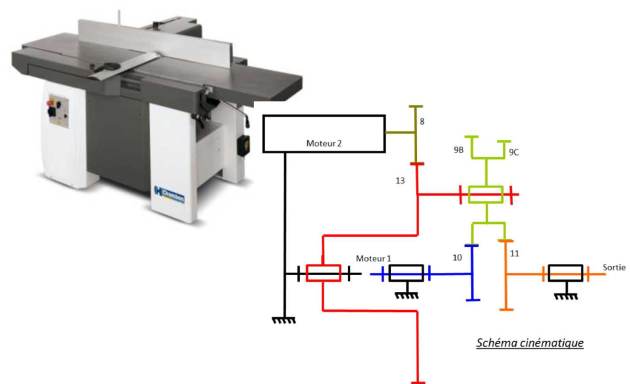
Le boîtier de commande étudié permet de transmettre, par l'intermédiaire d'un réducteur, le mouvement de rotation des deux moteurs 1 et 2 a un arbre de sortie. Cet arbre de sortie est lié à l'outil.
Les différentes configurations (moteurs en fonctionnement ou non) permettent d'obtenir plusieurs rapports de réduction possibles, et ainsi plusieurs vitesses possibles pour l'outil.
Question
Déterminer, en fonction des nombres de dents des roues dentées, la relation entre \({\omega_{M1/0}}\), \({\omega_{M2/0}}\) et \({\omega_{S/0}}\).
Solution
On a \({{\omega }_{S/0}}={{\omega }_{11/0}}\), \({{\omega }_{M1/0}}={{\omega }_{10/0}}\) et \({{\omega }_{M2/0}}={{\omega }_{8/0}}\)
Considérons le train 13-8 : \({{\omega }_{M2/0}}=-\frac{{{Z}_{13}}}{{{Z}_{8}}}{{\omega }_{13/0}}\)
Considérons le train 13-10-11-9 : Ce train est épicycloïdal, avec pour satellite 9, pour porte satellite 13 et pour planétaires 11 et 10. Donc \(\lambda =\frac{{{\omega }_{11/13}}}{{{\omega }_{10/13}}}={{\left( -1 \right)}^{2}}\frac{{{Z}_{10}}.{{Z}_{9C}}}{{{Z}_{9B}}.{{Z}_{11}}}\)
Par ailleurs on a \(\lambda =\frac{{{\omega }_{11/0}}-{{\omega }_{13/0}}}{{{\omega }_{10/0}}-{{\omega }_{13/0}}}\)
On peut alors écrire : \(0={{\omega }_{11/0}}+{{\omega }_{13/0}}\left( \lambda -1 \right)-\lambda {{\omega }_{10/0}}\) soit \(0={{\omega }_{S/0}}+{{\omega }_{13/0}}\left( \lambda -1 \right)-\lambda {{\omega }_{M1/0}}\).
Avec la première relation : \({{\omega }_{S/0}}-\frac{{{Z}_{8}}}{{{Z}_{13}}}{{\omega }_{M2/0}}\left( \lambda -1 \right)-\lambda {{\omega }_{M1/0}}=0\)
Question
Déterminer, après avoir formulé l'hypothèse qui convient, la relation entre les \({Z_i}\) liée aux conditions géométriques de montage des roues dentées.
Solution
Dans le cas où toutes les roues dentées ont le même module m : \(\Rightarrow {{D}_{i}}=m{{Z}_{i}}\), on a alors la distance entre l'axe de rotation propre du satellite et l'axe de rotation de la sortie qui vaut :
\(E=\frac{m}{2}\left( {{Z}_{11}}+{{Z}_{9C}} \right)=\frac{m}{2}\left( {{Z}_{10}}+{{Z}_{9B}} \right)\)