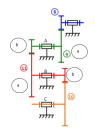
Monte charge
Présentation
Le monte-charge représenté ci-contre utilise un moteur (1500 tr/min) associé à un réducteur du fabricant DEMAG pour enrouler un câble sur un tambour et faire ainsi monter une charge.
La représentation du réducteur sous forme de schéma cinématique, est donnée ci-après.
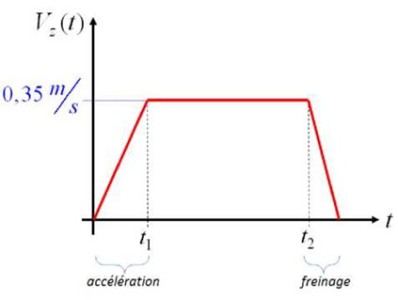
Pour obtenir un temps de montée minimal, tout en limitant la norme de l'accélération pendant le démarrage qui pourrait être à l'origine de dégâts sur la charge transportée, on impose le profil de vitesse suivant.
Objectif : Valider le choix du concepteur du monte-charge d'utiliser ce réducteur
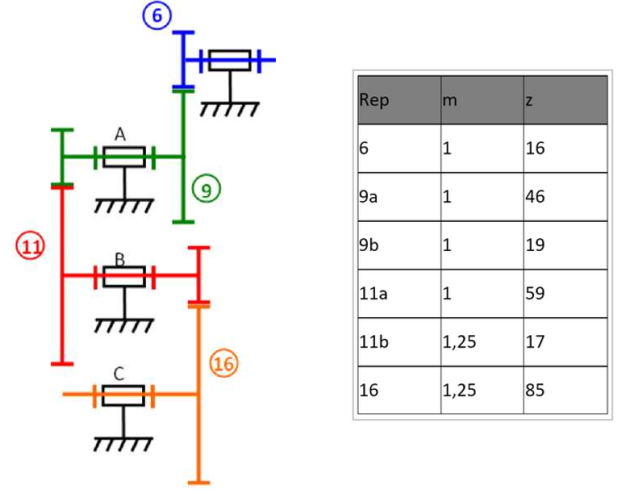
Caractéristiques des roues dentées :
Question
Repérer les roues dentées indicées a et b.
Question
Donner l'expression du rapport de réduction du réducteur. Faire l'application numérique.
Solution
Si on veut que chacun des étages du train d'engrenage réduise la vitesse de rotation, il faut :
• la roue dentée 16 soit liée à l'arbre de sortie du réducteur ;
• la roue dentée 6 soit liée à l'arbre d'entrée du réducteur ;
\(i = \frac{{{\omega _{S/2}}}}{{{\omega _{e/2}}}} = \frac{{{\omega _{16/2}}}}{{{\omega _{6/2}}}} = {\left( { - 1} \right)^3}\frac{{{Z_6}.{Z_{9b}}.{Z_{11b}}}}{{{Z_{9a}}.{Z_{11a}}.{Z_{16}}}}\)
AN : \(i = - 0,022\)
On fait l'hypothèse que pendant toute la montée de la charge, le diamètre d'enroulement des spires sur le tambour reste constant et est égal à 20 cm.
Question
Déterminer la vitesse de rotation du tambour, en tr/min, permettant d'obtenir le profil de vitesse de la charge imposé. Conclure quant au choix du concepteur d'utiliser ce réducteur.
Solution
\({V_Z} = R.{\omega _{tambour}} \Rightarrow {\omega _{tambour}} = \frac{{{V_Z}}}{R}\) or \({V_Z} = 0.35 m/s\) donc \({\omega _{tambour}} = \frac{{0.35}}{{0.1}} = 3.5 rad/s\) soit \({N_{tambour}} = 33,4 tr/min\)
\({N_{moteur}} = 1500 tr/min\) soit \(\left| {{N_{tambour}}} \right| = 1500x0.022 = 33 tr/min\).
Le couple moteur-réducteur choisit par le concepteur du monte-charge permet bien d'obtenir le profil de vitesse de la charge imposé.