Davina & Friends Learn To Subtract

Role reversal is the best description of my rethinking. I gradually became an adviser and a listener rather than an instructor. I became the learner, the children the teachers. My mind was open to new approaches, new ideas, new concepts. I began to realise that my way was not necessarily the only correct way.
[Shuard et al, Calculators, Children & Mathematics, 1991, page 45]

Background

• Every child had their own calculator and was encouraged to use it. Many of the Calculating Changes activities were used regularly.
• We set up a classroom shop from the beginning of the year. Objects were brought from home and were marked with their true supermarket price. The money in our shop was MAB 10. The flats were the dollars.
  The children visited the shop in groups, sometimes under the supervision of a helping mum, and took turns as the 'buyer', the 'cashier' and the 'packer'. The buyer had $10 to spend and was allowed to purchase up to three items; the cashier worked out the total on the calculator, accepted the money and worked out the change with MAB 10; the packer assisted in this calculation.
• The trading games Win A Flat, and later Lose A Flat, were introduced from the first week of the year.
• I have internalised, and use frequently, the two questions:
  
  • Can you show me how you did that?
  • Can you do it another way?
  I have found these very powerful because I rarely have to tell a child whether they are right or wrong. I simply have to congratulate them on the intelligence of their thought.

Children's Methods

However, to begin with, only one was offered. We talked about what they thought the symbols meant. 137 is a number, 48 is a number, - means take away…

So what do you think you have to do?
…
Well go and do it. You can use anything in the room to help you.

My second observation was, as expected, that some children subtracted the smaller digit from the larger regardless of 'sense'.
This is where the second question, Can you check it another way?,caused these children to be put into the positive conflict situation of having two different answers to the same question.
In general children using the 'subtract smaller from bigger regardless' strategy reached for the calculator to check their first response and preferred the calculator answer to their own. Of course this didn't tell them how to work out the exercise, but it did make them far less sure of their initial strategy, which left the way open for future consideration of other strategies.

My third observation, and the one which encouraged me to become the learner, relates to the methods the children developed and used over time; about two to three months!

Davina and Maree

Davina (Year 3) was the first to explain her method to me. She used MAB 10 to solve:

137

- 48

She was consistently writing correct answers in the space provided, but showing no working of any sort. Our conversation went like this:

Can you show me how you did that one?
Well first you make the big number with the wood like this.

(She neatly arranged one flat, three sticks and seven minis side by side.)

Then you make the little number and stack it on top.

(Four sticks and eight minis were placed neatly on top.)

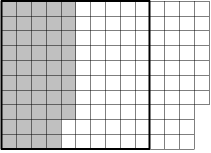
The answer is what's left uncovered.

How elegant! Given this context, is it surprising that she showed no working out?

That's great Davina, but what would you do if you didn't have any
wood?
Oh, I'd just put a picture of it in my head.

A little later I asked Davina to show her method to the class.

An effective way of helping children to refine their methods is to encourage them to share their methods with others; children are often able to incorporate other children's ideas into their own methods of calculation.
[Shuard et al (1991), page 33]

Generally speaking, the children were impressed with Davina's solution, but Maree (Year 3) added to our thoughts by explaining that her method was …a bit like that only you don't have to make the two numbers. She explained that she had made the first number with wood and then counted along it until she reached the second number. She placed her finger on that point and …everything past your finger is the answer.

So now we had Davina's Cover-up Method and Maree's Pointing Method. The majority of the children seemed to prefer Davina's method. It certainly helped to fill a vacuum for those children who had found fault with the previously described strategy of 'subtract smaller from bigger regardless'.

I was just fascinated that twenty-eight Year 2 and 3 children were merrily tackling the type of subtraction exercise which, with traditional teaching methods, would leave many Year 4 children floundering. And they didn't need a written algorithm to obtain a correct answer.

Aaron and Rodney

Over the next couple of weeks the story continued. Aaron (Year 3) had for some time only been able to explain to me that …I just do them in my head. Finally we isolated the process. Applying his thought to the previous problem of 137 - 48, he would argue:

137 - 40 = 97, then 97 - 8 = 89 and write down his answer.

So no written algorithm for him either and he demonstrated that he could do that sort of arithmetic in the situation of four digit numbers subtract three digit numbers. When I gave him the chance to explain it, the other children politely accepted his reasoning , but the mental gymnastics involved were too much for most of them at this stage.

Perhaps that was to be the last revelation … but no. Some time later I discovered that Rodney (Year 2) had developed another method. In the case above he realised that he couldn't take the 8 away from the 7 in the units column, so he first took it away from one of the tens in the tens column. Then he added the left-overs to the units which were yet to be used, to obtain his answer for the units column.

So, 10 - 8 = 2. Add this to the 7 which hasn't been used to make 9 as the units part of the answer.

The idea results from a natural shortcut the children use when playing Lose-A-Flat. (Perhaps we have difficulty seeing it because we usually ask children to play the game and less often play it ourselves.)

Rodney then repeated his process in the tens column, remembering that he had only two tens left in the top number. Therefore he took the 4 tens away from the available 100 and added the 6 tens left to the two unused tens waiting in the tens column.

That is 10(tens) - 4(tens) = 6(tens). Add these to the 2 tens which haven't been used in the tens column to obtain 8 as the tens part of the answer. You can almost 'hear' the mental picture of place value he has built up using the MAB.

It is possible to build a written algorithm which matches Rodney's work and looks similar to the more standard ones. You might like to try. Rodney did in fact do some recording to aid his thinking, but did not refine a written algorithm.

Teacher Development Activities

1. Play Win A Flat and Lose A Flat with the participants arranged in groups of 3. This will take at least 30 minutes. Rules and materials are at the link shown, or, if you have access to the Maths300 site (http://www.curriculum.edu.au/maths300) they can also be found in the Additonal Resources section of Lesson 35, Nine & Over.
2. Hand out copies of this story. Append the story Violet Blossoms. Ask individuals to read the story to themselves and allow informal discussion to develop.
3. Firstly in the groups of 3, and then as a whole group discuss:

   If you were this teacher, how would you proceed for the second half year.
   At what stage (if at all) would you introduce the required formal subtraction algorithm?
   If you introduced it, how would you present it to the class?

4. Distribute the Appendix to this story and repeat the read/informal discuss approach.
5. Conclude by asking each particpant to write down any ways in which the session will influence their future teaching practice, if at all. This is intended as private self-evaluation, but can be voluntarily shared if you wish.