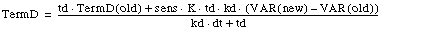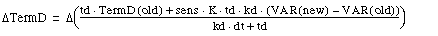Detailed PID Equations
(Original Document)
About us
Introduction
The PID algorithm uses the loop controller parameters as well as the intermediate variables and the following functions.
Intermediate variables and functions:
Variable/Function
Description
TermP
Proportional action value.
TermI
Integral action value.
TermD
Derived action value.
TermFF
Feed forward action value (disruption compensation).
(new)
Indicates a calculated value during the current execution of the algorithm.
(old)
Indicates a value calculated during the previous execution of an algorithm.
kp
Proportional gain. This user parameter can be specified either on a physical scale or on a standardized scale:
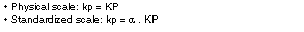K
Integral and derived action gains. The gain varies according to the loop controller structure (mixed or parallel) and the presence of the proportional action:
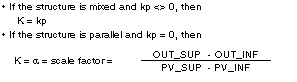VAR
Variable used in the derived action formula. Its value depends on the "Derived action" parameter:
  • VAR = PV if the derived action is on the process value.
  • VAR = DEV if the derived action is in the deviation.
Direction
  • Direction = +1 if action is direct. A positive deviation (PV - SP) leads to an output increase.
  • Direction = -1 if action is inverse. A positive gap (PV - SP) leads to an output decrease.
T_ECH
Sampling Period
Limit function
Corrector output limit function.
Absolute Form of the Algorithm
If Ti = 0, the absolute form of the algorithm is used. The loop controllers are of type P or PD.
OUT = TermP + TermD + TermFF + OUTBIAS
OUTD = OUTP(new) - OUTP(old)
OUT = limit (OUT) (not implemented)
Incremental Form of the Algorithm
If Ti <> 0, the incremental form of the algorithm is used. The loop controllers are of type PID.
OUT = OUT(old) + OUTD(new), default mode
OUT = RCPY + OUTD(new), actuator position copy mode. This mode is used in certain special cases where the actuator position can be different from the calculated output of the PID (SERVO output, cascaded loop or auto selector loop).
OUT = limit (OUT)
Antisaturation
The integral antisaturation mechanism is implicit in the algorithm.
Pure Integral Mode
The loop controller is able to work in pure integral mode (kp = 0). In this case the equations are as follows:
OUTD = TermI + TermFF
OUT = OUT(old) + OUTD(new), default mode
OUT = RCPY + OUTD(new), actuator position copy mode
OUT = limit (OUT)
Execution Monitoring
The system indicates a processing error in the following cases:
In each case, the error is considered to be serious. The loop output is frozen, while errors are signaled in the status words.