There are numerous approaches to adjusting a PID's parameters. We recommend Ziegler & Nichols' method, of which there are two variants:
-
closed loop adjustment
-
open loop adjustment
Before implementing either method, one must determine the direction of the PID's action:
-
if increasing the OUT output triggers an increase of the PV value, reverse the PID's direction (KP > 0)
-
Inversely, if increasing the OUT output provokes a decrease of the PV value, use the PID in the forward direction (KP < 0)
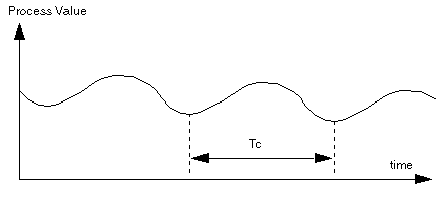
This method consists in issuing a proportional command (Ti = 0, Td = 0) in order to excite the process by increasing the gain until reaching oscillation, after having applied a step to the PID loop controller setpoint. Then, it's only a matter of measuring the critical gain value (Kpc) that triggered the unabsorbed oscillation, as well as the oscillation period (Tc) in order to derive the values ensuring optimal adjustment of the loop controller
.
Depending on the loop controller type (PID or PI), coefficients are adjusted with the following values:
|
-
|
Kp
|
Ti
|
Td
|
|
PID
|
Kpc/1,7
|
Tc/2
|
Tc/8
|
|
PI
|
Kpc/2,22
|
0,83 x Tc
|
-
|
where Kp = proportional gain, Ti = integration time and TD = derivative time.
NOTE: This adjustment method produces an extremely dynamic command which may provoke undesired overflows when changing the setpoints. If so, decrease the gain value until you obtain the proper behavior.
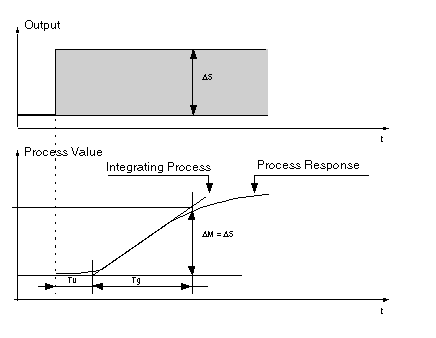
After setting the Loop Controller in Manual mode, apply a step on its output and assimilate the beginning of the process result with an integrating process with pure delay.
.
The Tu time value is determined by intersecting the line representing the integrating process with the time axis. Tg time is then defined as being the time required by the controlled variable (process value) to fluctuate with the same amplitude (expressed as a scaling percentage) as the loop controller output.
Depending on the loop controller type (PID or PI), coefficients are adjusted with the following values:
|
-
|
Kp
|
Ti
|
Td
|
|
PID
|
-1.2 Tg/Tu
|
2 x Tu
|
0.5 x Tu
|
|
PI
|
-0.9 Tg/Tu
|
3.3 x Tu
|
-
|
where Kp = proportional gain, Ti = integration time and TD = derivative time.
NOTE: Be mindful of measuring units. If the adjustment is done in Control Expert, multiply the KP value by 100.
This adjustment method also produces an extremely dynamic command which may provoke undesired overflows when changing the setpoint. If so, decrease the gain value until you observe the desired behavior. The advantage of this method lays in that it does not require any assumption as to the nature and order of the process. It applies as well to stable processes as to truly integrating processes. This method proves particularly useful in the context of slow processes (i.e. the glass industry), since the user needs only the beginning of the response to adjust the Kp, Ti and Td coefficients.