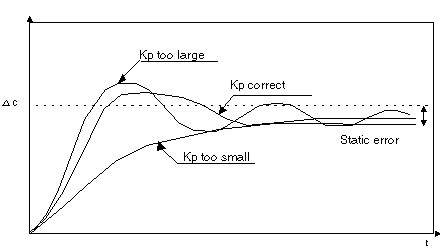
Proportional Action Influence
Proportional action enables the process response speed to be matched. The higher the gain, the more the response will accelerate and the static error will reduce (in purely proportional terms), but the greater the deterioration of stability will be. A compromise between speed and stability must be found. The following is the influence of integral action on the process response.
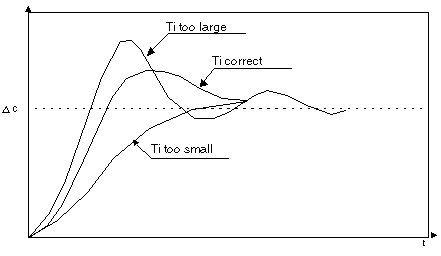
Influence of Integral Action
Integral action ensures that static error (the deviation between the process value the and setpoint) is canceled out. The higher the integral action (Ti small), the greater the acceleration of the response and the more stability deteriorates. A compromise must be found between speed and stability. The influence of integral action on process response at a grade is as follows.
NOTE: Small Ti represents a high integral action.
Kp = proportional gain, Ti = integration time and TD = derivative time.
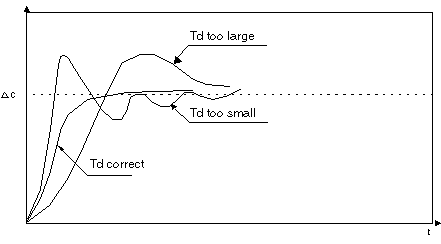
Influence of Derivative Action
Derivative action is anticipatory. It adds a term that accounts for the speed variation of the difference, which enables anticipation by accelerating the process response when the deviation increases, and slowing it down when the deviation decreases. The higher the derivative action (large Td), the more the response accelerates. Here again, a compromise between speed and stability must be found. The influence of derivative action on the process response at a division is as follows.
Limits of PID Process Control
If the process is assimilated to a first command with pure time delay, of transfer function:
with:
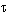
= model delay,
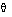
= model time constant,
The process control performances are dependent on the ratio

PID process control is suitable in the following area: 2 < =

< 20
For
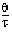
<2, meaning fast loops (
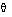
small) or for processes with large delays (

large) the PID process control is not suitable and more advanced algorithms must be used.
For

> 20, a threshold process control with hysteresis is sufficient.

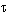 = model delay,
= model delay, 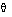 = model time constant,
= model time constant,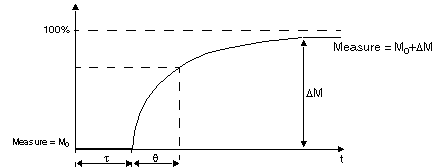

 < 20
< 20 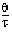 <2, meaning fast loops (
<2, meaning fast loops (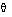 small) or for processes with large delays (
small) or for processes with large delays ( large) the PID process control is not suitable and more advanced algorithms must be used.
large) the PID process control is not suitable and more advanced algorithms must be used.  > 20, a threshold process control with hysteresis is sufficient.
> 20, a threshold process control with hysteresis is sufficient.