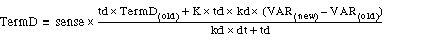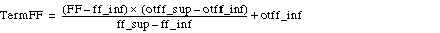Detailed equations
Original instructions
About us
Overview
The detailed equations are shown for the following situations are shown in this section:
Convention
Various variables and functions are used in the following equations. The variables corresponding to the parameters of the function block are not newly described.
The most important Interim variables and the functions used are described in the following tables.
Explanation of the interim variables
An explanation of the most important interim variables can be found here.
Interim variable
Meaning
DEV_WGH
DEV_WGH = PV - (1 - ovs_att) * SP
dt
Time elapsed since the last function block execution.
K
Gain of the integral and differential components.
The gain varies according to the structure of the function block (mixed or parallel) and depends on whether the proportional component is assigned or not.
  • If mix_par = 0 (mixed structure) and kp <> 0, K = kp applies
  • If mix_par = 1 (parallel structure) or kp – 0, the following applies:)
(new)
Value which is calculated on current execution of the function block
(old)
Value which is calculated on previous execution of the function block
OUTc
Before limitation of calculated output value
sense
Control setting
TermAW
Value of the bumpless anti-windup measure
TermD
Value of the differential component
TermFF
Value of the feed forward component (disturbance compensation)
TermI
Value of the integral component
TermP
Value of the proportional component
VAR
To calculate the variable used by the differential component.
Its value depends on the pv_dev parameter :
  • If pv_dev = 0, VAR = PV
  • If pv_dev = 1, VAR = dev
Explanation of the functions
An explanation of the most important functions can be found here.
Function
Meaning
Control setting
The control setting has the following directions of action:
  • +1
    This is an opposite action (rev_dir = 1) i.e. a positive deviation (PV - SP) generates an increasing output value
  • -1
    This is a direct action (rev_dir = 0) i.e. a positive deviation (PV - SP) generates a reduction in the output value
Function Δ
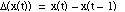’Limit’
Limiting function for the function block output
Absolute algorithm
The following equations apply for PD controllers ( ti = 0);
Value of the proportional component TermP
Value of the differential component TermD
Value of the feed forward component TermFF