Correction à avance de phase
Correction à retard de phase
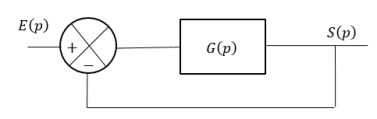
Considérons un système de fonction de transfert \(G\left( p \right)\) placé dans une boucle à retour unitaire avec : \(G\left( p \right) = \frac{{100}}{{{{\left( {p + 1} \right)}^2}}}\)
Les performances attendues sont les suivantes :
- Marge de phase \(M\varphi=45°\)
Question
Etablir le schéma bloc du système
Question
Déterminer la marge de phase de ce système (Graphiquement et analytiquement). Conclure quant à la capacité du système à respecter la marge de phase proposée
Solution
Rappel : on étudie la FTBO pour étudier les marges de stabilité. Tracé avec K=1
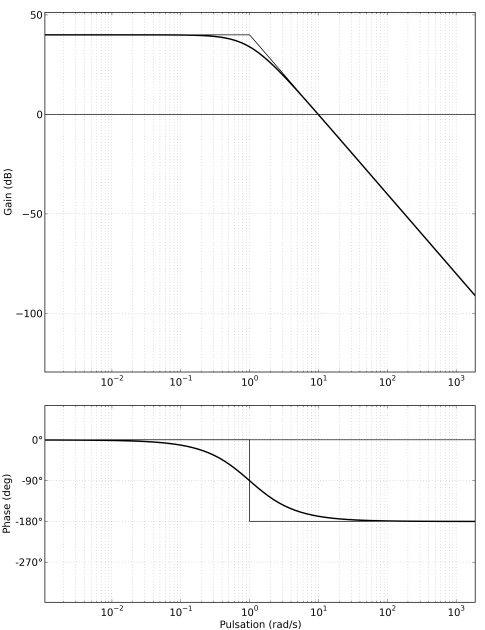
Graphiquement :
On a \({\omega _{{c_0}}} = 10\;rad/s\) la marge de phase est de l'ordre de 10°
Analytiquement :
A la pulsation de coupure, le gain doit être nul :
\({G_{dB}}\left( {{\omega _{{c_0}}}} \right) = 0\) soit \(\left| {H\left( {j{\omega _{{c_0}}}} \right)} \right| = 1\)
\(\left| {H\left( {j{\omega _{{c_0}}}} \right)} \right| = \frac{{100}}{{\left| {{{\left( {j{\omega _{{c_0}}} + 1} \right)}^2}} \right|}} = \frac{{100}}{{{{\left| {j{\omega _{{c_0}}} + 1} \right|}^2}}} = \frac{{100}}{{1 + {\omega _{{c_0}}}^2}}\)
\(\frac{{100}}{{1 + {\omega _{{c_0}}}^2}} = 1\)
\({\omega _{{c_0}}} = \sqrt {99} = 9,95\;rad.{s^{ - 1}}\)
\(M\varphi = \pi + \arg \left[ {\frac{K}{{{{\left( {1 + j{\omega _{{c_0}}}} \right)}^2}}}} \right] = \pi - \arg \left[ {{{\left( {1 + j{\omega _{{c_0}}}} \right)}^2}} \right] = \pi - 2\arg \left( {1 + j{\omega _{{c_0}}}} \right) = \pi - 2{\tan ^{ - 1}}{\omega _{{c_0}}}\)
\(M\varphi = \pi - 2{\tan ^{ - 1}}9,95 = 0,2\;rad = 11^\circ\)
Il est donc nécessaire de corriger le système afin d'augmenter la marge de phase.
Il faut augmenter la marge de phase de \(45 - 11 = 34^\circ\) à la pulsation \({\omega _{{c_0}}} = 9,95\)
On ajoute au système un correcteur à avance de phase \(C\left( p \right) = \frac{{1 + aTp}}{{1 + Tp}}\;\) avec \(a > 1\) placé en cascade. Nous allons régler ce correcteur dans le but de répondre au critère de stabilité demandé.
Question
Rappeler le diagramme de Bode du correcteur. Donner l'expression de la pulsation \({\omega _{max}}\) à laquelle la phase est maximale ?
Solution
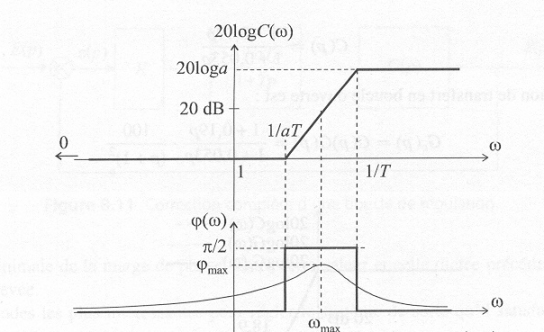
\({\omega _{max}} = \frac{1}{{T\sqrt a }}\) avec \({\rm{log}}({\omega _{max}}) = \frac{1}{2}\left( {log\left( {\frac{1}{T}} \right) + log\left( {\frac{1}{{aT}}} \right)} \right)=\frac{1}{2}log{\left( {\frac{1}{{a{T^2}}}} \right)^{}} = log{\left( {\frac{1}{{\sqrt {a{T^2}} }}} \right)^{}}\)
Question
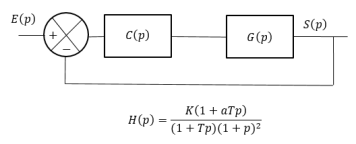
Etablir le schéma bloc du système corrigé et sa nouvelle FTBO notée \(H\left( p \right)\)
On rappelle l'expression de la phase maximale \({\varphi _{max}} = {\sin ^{ - 1}}\left( {\frac{{a - 1}}{{a + 1}}} \right)\) en \({\omega _{max}}\).
Question
Régler le correcteur dans le but de répondre au cahier des charges
Solution
On place la phase maximale en \( {\omega _{{c_0}}}\;:\)
\(\frac{1}{{T\sqrt a }} = {\omega _{{c_0}}}\) soit \(T = \frac{1}{{{\omega _{{c_0}}}\sqrt a }}\)
On choisit a afin d'obtenir une augmentation de phase \( \theta\) de 34°, soit 0,59 rd : \({\sin ^{ - 1}}\left( {\frac{{a - 1}}{{a + 1}}} \right) = \theta\)
\(\frac{{a - 1}}{{a + 1}} = \sin \theta\) soit \(a - 1 = a\sin \theta + \sin \theta\) donc \(a - a\sin \theta = 1 + \sin \theta\)
\(a = \frac{{1 + \sin \theta }}{{1 - \sin \theta }} = \frac{{1 + \sin 0,59}}{{1 - \sin 0,59}} = 3,54\)
Donc : \(T = \frac{1}{{{\omega _{{c_0}}}\sqrt a }} = \frac{1}{{9,95\sqrt {3,54} }} = 0,053\)
Question
La marge de phase obtenue est-elle exactement de 45° ? Justifier. Donner finalement la fonction de transfert du correcteur à avance de phase permettant au système de répondre aux critères de performances attendus
Solution
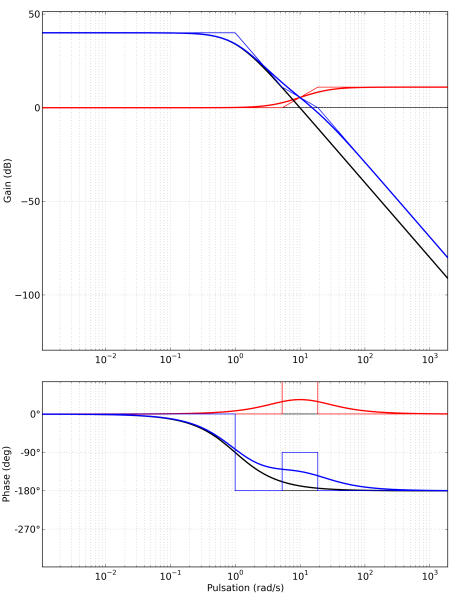
Le gain étant modifié par ce correcteur, ${\omega _{{c_0}}}$ est légèrement augmentée et la phase n'est donc pas corrigée d'autant qu'il le faudrait.
$C\left( p \right) = \frac{{1 + 0,19p}}{{1 + 0,053p}}$