Choix d'un type de correcteur
Choix d'un type de correcteur
Connaissant la fonction de transfert en boucle ouverte \(G(p)\) de deux systèmes différents, on se propose de choisir un correcteur\( C(p)\) de façon à respecter certains critères du cahier des charges :
Système n°1 : | Système n°2 : |
|---|---|
\({G_1}(p){\rm{ }} = {\rm{ }}\frac{1}{{p.(1 + 0,2\,p)}}\) | \({G_2}(p){\rm{ }} = {\rm{ }}\frac{1}{{{{(1 + 0,1\,p)}^2}}}\) |
Performances exigées : Écart de traînage en boucle fermée \({\varepsilon _v} < 0,05\) , en réponse à une entrée en rampe unitaire. Marge de phase de 45°. | Performances exigées : Écart de position en boucle fermée : \({\varepsilon _S} = 0\) Marge de phase de 45°. |
Trois types de correcteurs sont proposés :
- Correcteur proportionnel : \(C_p(p){\rm{ }} = {\rm{ }}K_p\)
- Correcteur proportionnel intégral (PI) : \(C_{pi}(p){\rm{ }} = {\rm{ }}\frac{{1 + \tau \,p}}{{\tau \,p}}\)
- Correcteur à retard de phase (ou intégral approché) : \(\quad C_{rp}\,(p) = \frac{{1 + \tau \,p}}{{1 + \,b\tau \,p}}\quad\) avec \(b > 1\).
Question
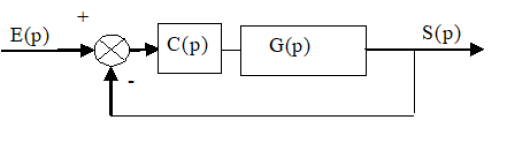
Q1. Donner la représentation dans les plans de Bode du correcteur PI en faisant apparaître ses éléments caractéristiques.
Solution
\(Cpi(p){\rm{ }} = {\rm{ }}\frac{{1 + \tau \,p}}{{\tau \,p}}\)
Question
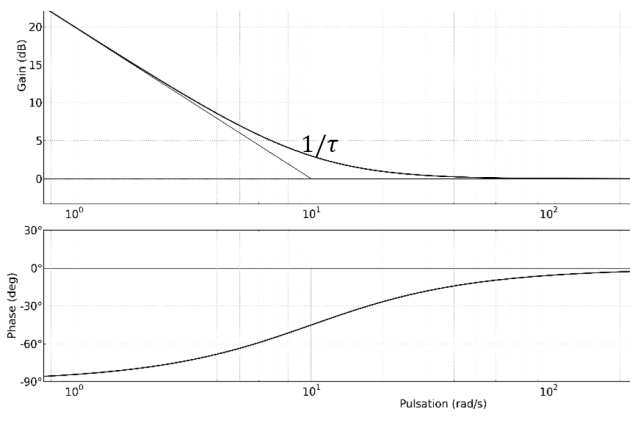
Q2. Donner la représentation dans les plans de Bode du correcteur à retard de phase en faisant apparaître ses éléments caractéristiques.
Solution
\(\quad Crp\,(p) = \frac{{1 + \tau \,p}}{{1 + \,b\tau \,p}}\quad\) avec \(b > 1\).
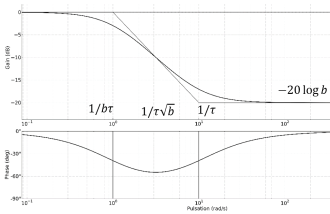
D'après le cours \({\varphi _{MAX}} = {\rm{arcsin}}\left( {\frac{{1 - b}}{{1 + b}}} \right)\)
Question
Q3. Analyser chacun des deux systèmes ainsi que les performances exigées associées, et proposer un choix de correcteur qui permettrait de répondre à ce cahier des charges.
Solution
Pour \(G_2(p)\), on veut un écart statique nul ; la seule solution est de prévoir un intégrateur dans la boucle ; on choisira donc le correcteur proportionnel intégral \( C_{pi}(p)\).
Pour\( G_1(p)\), on veut respecter un certain écart de traînage \({\varepsilon _v} < 0,05\) ; ceci peut se faire avec le correcteur proportionnel \(Cp(p)\) car pour ce système de classe 1, on a \({\varepsilon _v} = \frac{1}{{K_{BO}}}\) ;
néanmoins si le gain est trop important, la marge de phase risque de ne pas être respectée ;
dans ce cas il faudra associer le correcteur à retard de phase \( Crp(p)\) au correcteur \(Cp(p)\) pour utiliser la baisse de gain apportée à haute fréquence (le correcteur PI ne peut pas être utilisé car le déphasage apporté par son intégrateur conduirait à l'instabilité du système).
Système n° 2 :
\({G_2}(p){\rm{ }} = {\rm{ }}\frac{1}{{{{(1 + 0,1\,p)}^2}}}\)
Question
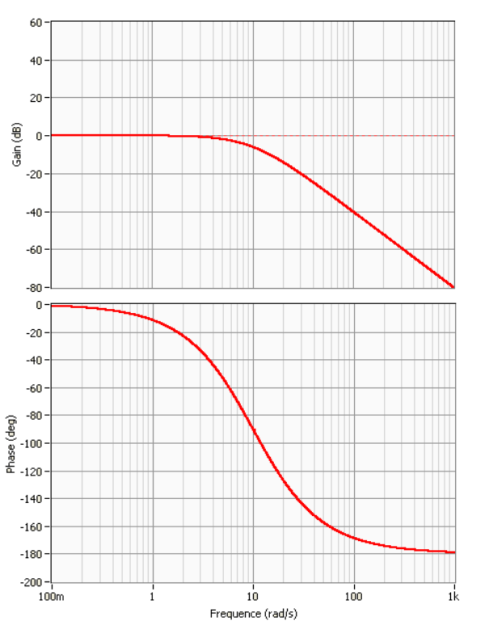
Q4. A l'aide du diagramme de Bode fourni, déterminer le correcteur proportionnel \({K_2}\) qui permet d'obtenir une marge de phase \(M\varphi = 50°\). Appliquer à ce système n°2 muni de la correction proportionnelle \({K_2}\), le correcteur \(C_{pi}(p)\) et déterminer la constante de temps \(τ\) de ce correcteur pour ne pas modifier de plus de 5° la marge de phase réglée avec le correcteur proportionnel. Tracer le diagramme de Bode de la FTBO du système corrigé complet.
Solution
Déterminons le correcteur proportionnel
Déterminons le correcteur proportionnel \(K_2\) pour obtenir \(M\varphi = 50°\) : Le déphasage vaut \((-180° + 50° ) = -130°\) à la pulsation \({\omega _{c0dB}} = 20\;rd/s\). A cette pulsation, le gain vaut \(– 15 dB\) ;
Pour obtenir la marge de phase de 50°, il faut donc translater la courbe de gain de + 15 dB ;
Cela revient à multiplier la FTBO par \(K_2 = {10^{15/20}} = 5,6\)
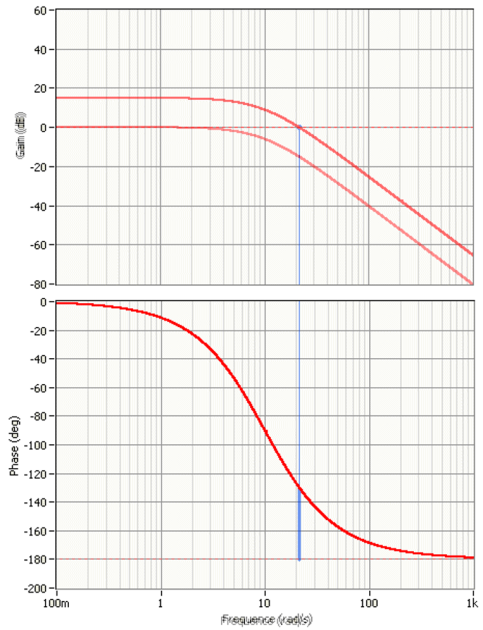
Mettons en place le correcteur PI :
Positionnons-le de façon à ce que la cassure de ce correcteur soit placée à une pulsation 10 fois plus faible que la pulsation à laquelle le réglage de la marge de 50° a été effectué :
Donc \(1/T =\frac{ \omega_{c0dB}}{10} = 20/10 = 2 rd/s\) d'où \(T = 10/20 = 0,5\) s
on obtient : \(Cpi(p){\rm{ }} = {\rm{ }}\frac{{1 + 0,5.\,p}}{{0,5.\,p}}\)
tracé du système corrigé complet : \(FTB{O_2}(p){\rm{ }} = {\rm{ 5}}{\rm{,6}} \cdot \frac{{1 + 0,5.\,p}}{{0,5.\,p}}{\rm{ }} \cdot \frac{1}{{{{(1 + 0,1\,p)}^2}}}\)
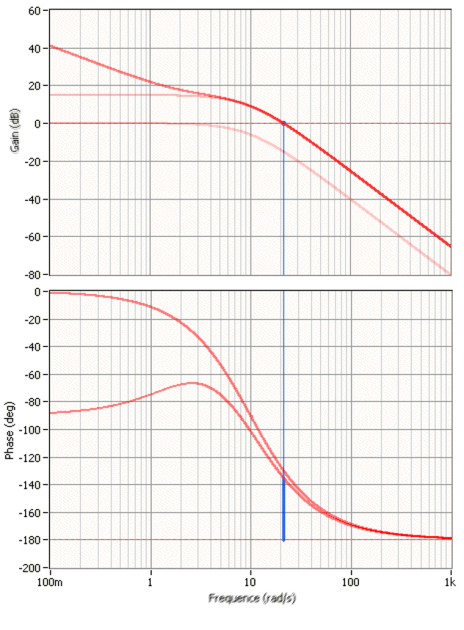
Système n°1 :
\({G_1}(p){\rm{ }} = {\rm{ }}\frac{1}{{p.(1 + 0,2\,p)}}\) et \({K_1}.\;{G_1}\left( p \right)\)
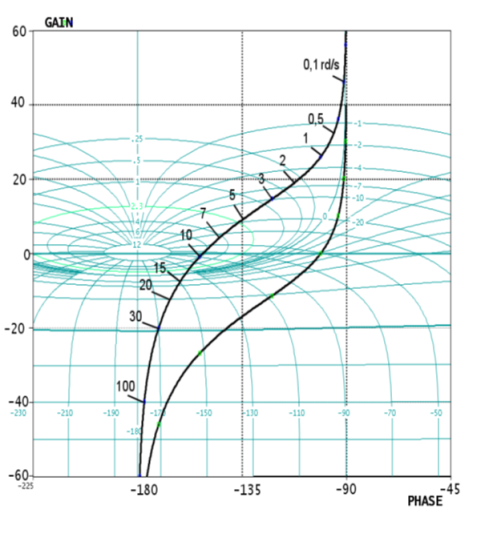
Question
Q5. Déterminer le correcteur proportionnel \({K_1}\) qui permet de respecter le critère de l'écart de traînage. Retrouver cette valeur graphiquement sur le diagramme de Black fourni de \(K_1.G_1(p)\). Vérifier que le critère de marge de phase n'est pas respecté dans ces conditions ; Appliquer à ce système n°1 muni de la correction proportionnelle \({K_1}\), le correcteur à « retard de phase » et choisir le paramètre \( b\) de ce correcteur pour respecter le critère de marge de phase. Choisir la constante de temps du correcteur pour ne modifier que faiblement le réglage de marge de phase effectué. Tracer l'allure de la FTBO corrigée sur le diagramme de Black fourni.
Solution
Déterminons le correcteur proportionnel
\(K_1\) pour obtenir \({\varepsilon _v} =0,05\), la FTBO possède un intégrateur, donc \({\varepsilon _v} =\frac{1}{{{K_{BO}}}}\) d'où : \({\varepsilon _v} =\frac{1}{{{K_{1}}}}\) donne : \(K_1 = \frac{1}{{0,05}} = 20\)
- vérification dans le diagramme de Black : la translation effectuée est de \( 20 log(20) = 26 dB\)
- Avec cette valeur \(K_1 = 20\), on obtient \(M\varphi=30°\) ce qui ne respecte pas le cahier des charges.
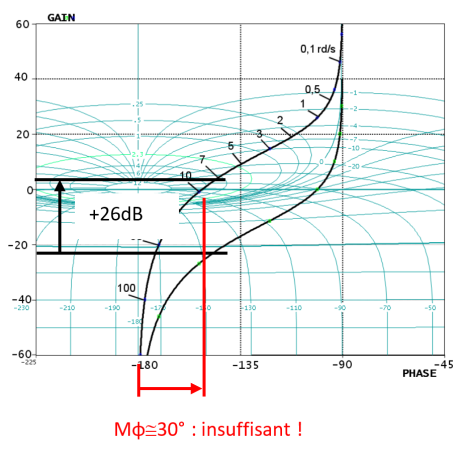
Déterminons le correcteur à retard de phase
pour cette valeur de \(K=K_1=20\), choisissons un correcteur à retard de phase qui va abaisser les valeurs de gain à la pulsation \(\omega_{-135}\) où on a \(Arg(K_1.G_1(j\omega)) = - 135°\),
il faut choisir la valeur de \(b\) telle que la courbe de gain s'abaisse de \( 20.log(b)\) à la pulsation \(\omega_{-135}\) .
- on choisit la cassure \(\frac{1}{T} \) du correcteur telle que \(\frac{1}{T} = \frac{\omega_{-135}}{10}\) ; d'où \(T = 2s\)
alors : \(Crp(p) = \frac{{1 + 2.p}}{{1 + 6,4.p}}\) et \(FTBO_1^{}(p) = 20 \cdot \frac{{1 + 2.p}}{{1 + 6,4.p}} \cdot \frac{1}{{p.(1 + 0,2.p)}}\).
Diagramme de Bode de la FTBO corrigée | Diagramme de Black de la FTBO corrigée |
|---|---|
|
|
Remarque : A propos du retard de phase
Pas malin de l'utiliser juste pour décaler la pulsation de coupure ! ! ! Le mieux serait d'utiliser un avance de phase de type \(\quad Cap\,(p) = K_a\frac{{1 + \tau \,p}}{{1 + \,b\tau \,p}}\quad\) avec \(b < 1\). On choisirait alors :
- on a \(\phi_m=-15°=sin \frac{1-b}{1+b}\)
- \( \omega_m=\frac{1}{\tau\sqrt{b}}=\omega_{0dB}\)
- reste à régler \(K_a\) de tel sorte que \(G_{db}(\omega_{0dB})\) reste nul....