Magic Arms V2
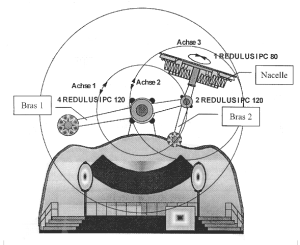
Le « magic arms » est un manège fabriqué par la société WAAGNER-BIRO. Ses mouvements simultanés autour de trois axes, désorientent les 39 passagers embarqués qui ne savent plus reconnaître le dessus du dessous pendant quelques minutes. L'entraînement en rotation des différents bras du manège est réalisé par des ensembles moteurs asynchrones - réducteur. Leur commande est assistée par un calculateur qui permet de développer des séquences variées de mouvements.
L'installation est composée d'une structure métallique d'environ 12 m de haut avec 2 bras mobiles (voir figure ci-dessous).

Dès que tous les passagers sont assis et attachés, le bras principal (bras 1) et le bras pivot (bras 2), liés l'un à l'autre au début du cycle, commencent à tourner. En même temps la nacelle tourne autour de son axe. Après 9 secondes, le maximum de hauteur est atteint et les 2 bras se désindexent et se mettent à tourner indépendamment l'un de l'autre.
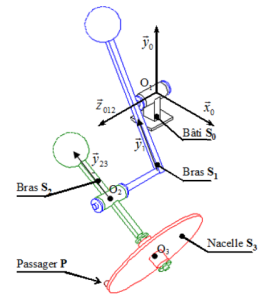
Dans cette étude nous nous intéresserons plus particulièrement au passager le plus sollicité. Le schéma ci-dessous donne la position de ce passager ainsi que les angles et les repères attachés aux différents solides.
Remarques:
un vecteur lié à un solide porte l'indice du solide ;
exemple : \(\overrightarrow{x_1}\) lié au solide 1 ;
un vecteur lié à plusieurs solides porte les indices des solides ;
exemple : \(\overrightarrow{z}_{012}\)commun à 0, 1 et 2.
\(R_0 (O_1, \overrightarrow{x_0}, \overrightarrow{y_0},\overrightarrow{z}_{012})\) est un repère lié au bâti \(S_0\).
\(R_1 (O_1, \overrightarrow{x_1}, \overrightarrow{y_1},\overrightarrow{z}_{012})\) est un repère lié au bras \(S_1\).
\(R_2 (O_2, \overrightarrow{x_2}, \overrightarrow{y}_{23}\overrightarrow{z}_{012})\) est un repère lié bras \(S_2\).
\(\overrightarrow{O_1 O_2} = -L_1 \overrightarrow{y_1} + a \overrightarrow{z}_{012}\) avec \(L_1=3,9~m\).
\(R_3 (O_3, \overrightarrow{x_3}, \overrightarrow{y}_{23}\overrightarrow{z}_3)\) est un repère lié à la nacelle \(S_3\).
\(\overrightarrow{O_2O_3}=-L_2 \overrightarrow{y}_{23}\) et \(\overrightarrow{O_3P}= - L_3 \overrightarrow{z_3}\), avec \(L_2 = 2,87~m\) et \(L_3=2,61~m\).
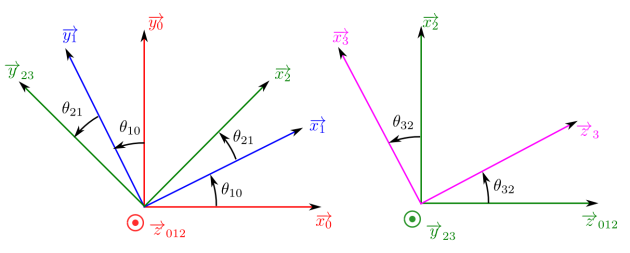
\(S_1\) est en rotation d'axe \((O_1, \overrightarrow{z}_{012})\) avec le solide \(S_0\). On pose \(\theta_{10}=(\overrightarrow{x_0},\overrightarrow{x_1})=(\overrightarrow{y_0},\overrightarrow{y_1})\).
\(S_2\) est en rotation d'axe \((O_2, \overrightarrow{z}_{012})\) avec le solide \(S_1\). On pose \(\theta_{21}=(\overrightarrow{x_1},\overrightarrow{x_2})=(\overrightarrow{y_1},\overrightarrow{y_2})\).
\(S_3\) est en rotation d'axe \((O_3, \overrightarrow{y}_{23})\) avec le solide \(S_2\). On pose \(\theta_{32}=(\overrightarrow{x_2},\overrightarrow{x_3})=(\overrightarrow{z}_{012},\overrightarrow{z_3})\).
Pour simplifier les notations, on posera \(\theta_{20}=(\overrightarrow{x_0},\overrightarrow{x_2})=(\overrightarrow{y_0},\overrightarrow{y_2})\)..
Question
Déterminer 2 figures géométrales permettant de représenter les angles de rotation \(\theta_{10}\), \(\theta_{21}\) et \(\theta_{32}\)
Question
Exprimer \(\left\{ \mathcal{V}_{1/0}\right\}_{O_1}\).
En déduire \(\left\{ \mathcal{V}_{1/0}\right\}_{P}\)
Solution
Réponse
\(\left\{ \mathcal{V}_{1/0} \right\}=\left.\begin{array}{c}~\\~\end{array}\right._{O_1}\left\{\begin{array}{l}\dot\theta_{10}\overrightarrow{z}_{012} \\ \overrightarrow{0}\end{array}\right\}\)
\(\left\{ \mathcal{V}_{1/0} \right\}=\left.\begin{array}{c}~\\~\end{array}\right._{P}\left\{\begin{array}{l}\dot\theta_{10}\overrightarrow{z}_{012} \\ \dot \theta_{10}\left( L_1 \overrightarrow{x}_1 + L_2 \overrightarrow{x_2} - L_3 \sin \theta_{32} \overrightarrow{y}_{23} \right)\end{array}\right\}\)
Question
Exprimer \(\left\{ \mathcal{V}_{2/1}\right\}_{O_2}\).
En déduire \(\left\{ \mathcal{V}_{2/1}\right\}_{P}\)
Solution
Réponse
\(\left\{ \mathcal{V}_{2/1} \right\}=\left.\begin{array}{c}~\\~\end{array}\right._{O_2}\left\{\begin{array}{l}\dot\theta_{21}\overrightarrow{z}_{012} \\ \overrightarrow{0}\end{array}\right\}\)
\(\left\{ \mathcal{V}_{2/1} \right\}=\left.\begin{array}{c}~\\~\end{array}\right._{P}\left\{\begin{array}{l}\dot\theta_{21}\overrightarrow{z}_{012} \\ \dot \theta_{21}\left( L_2 \overrightarrow{x_2} - L_3 \sin \theta_{32} \overrightarrow{y}_{23} \right)\end{array}\right\}\)
Question
Exprimer \(\left\{ \mathcal{V}_{3/2}\right\}_{O_3}\).
En déduire \(\left\{ \mathcal{V}_{3/2}\right\}_{P}\)
Solution
Réponse
\(\left\{ \mathcal{V}_{3/2} \right\}=\left.\begin{array}{c}~\\~\end{array}\right._{O_3}\left\{\begin{array}{l}\dot\theta_{32}\overrightarrow{y}_{23} \\ \overrightarrow{0}\end{array}\right\}\)
\(\left\{ \mathcal{V}_{3/2} \right\}=\left.\begin{array}{c}~\\~\end{array}\right._{P}\left\{\begin{array}{l}\dot\theta_{32}\overrightarrow{y}_{23} \\ -L_3 \dot \theta_{32} \overrightarrow{x}_3 \end{array} \right\}\)
Question
En utilisant la composition des mouvements, déterminer \(\left\{ \mathcal{V}_{3/0}\right\}_{P}\).
Solution
Réponse
\(\left\{ \mathcal{V}_{3/0} \right\}=\left.\begin{array}{c}~\\~\end{array}\right._{P}\left\{\begin{array}{l}\dot\theta_{20}\overrightarrow{z}_{012} + \dot \theta_{32} \overrightarrow{y}_{23}\\ L_1 \dot \theta_{10} \overrightarrow{x_1} + \dot \theta_{20}\left( L_2 \overrightarrow{x_2} - L_3 \sin \theta_{32} \overrightarrow{y}_{23} \right) - L_3 \dot \theta_{32} \overrightarrow{x}_3 \end{array}\right\}\)
Question
En déduire l'accélération \(\overrightarrow{\Gamma}(P,3/0)\).