Variateur à billes PIV

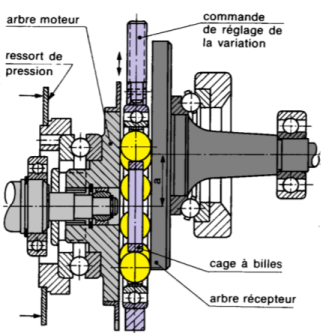
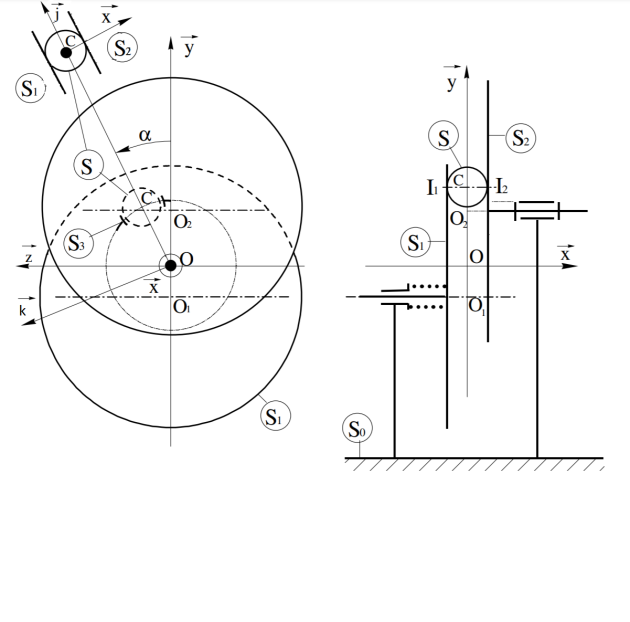
Le variateur de vitesse à billes de marque PIV dont la description détaillée est donnée transmet le mouvement de rotation entre un plateau moteur \(S_1\) et un plateau récepteur \(S_2\) par l'intermédiaire d'un ensemble de billes maintenues dans une cage \(S_3\).
La cage \(S_3\) est en liaison pivot d'axe \(\left( {O,\overrightarrow x} \right)\) avec le bâti. Afin de régler la vitesse du plateau récepteur \(S_2\), il est possible de déplacer la cage \(S_3\) par rapport au bâti selon l'axe \( \overrightarrow y\).
Le repère \(R\left( {O,\overrightarrow x,\overrightarrow y,\overrightarrow z} \right)\) est lié au bâti fixe \(S_0\) du variateur avec une origine \(O\) centre de la cage à bille \(S_3\).supposée pour notre étude fixe par rapport à \(S_0\) lors du fonctionnement.
Le plateau \(S_1\) est en liaison pivot d'axe \(\left( {{O_1},\overrightarrow x} \right)\) avec le bâti \(S_0\). Le plateau \(S_2\) est en liaison pivot d'axe \(\left( {{O_2},\overrightarrow x} \right)\) avec le bâti \(S_0\).
\(\overrightarrow {{O_1}{O_2}} = a\;\overrightarrow y\), \(\overrightarrow {{O_1}O} = \lambda \;\overrightarrow y\) où \(\lambda\) est le paramètre géométrique de réglage du variateur.
On pose \(\overrightarrow {\Omega ({S_1}/R)} = {\omega _1}\;\overrightarrow x\) et \(\overrightarrow {\Omega ({S_2}/R)} = {\omega _2}\;\overrightarrow x\)
Chaque bille \(S\), de rayon \(b\), roule sans glisser en \(I_1\) sur \(S_1\) et en \( I_2\) sur \(S_2\).
Le centre \(C\) de chaque bille est tel que \(\overrightarrow {OC} = r\;\overrightarrow i\) avec \({R_1}\left( {O,\overrightarrow i,\overrightarrow j,\overrightarrow z} \right)\) un repère lié à la cage \(S_3\).
On pose : \(\alpha = \left( {\overrightarrow y,\overrightarrow i} \right) = \left( {\overrightarrow x,\overrightarrow j} \right)\) et \(\overrightarrow {\Omega ({S_3}/R)} = \omega \;\overrightarrow x\)
Le corps \(S_2\), auquel on associe le repère \({{R}_{2}}(A,\overrightarrow{{{x}_{2}}},\overrightarrow{{{y}_{2}}},\overrightarrow{{{z}_{2}}})\) est en mouvement de rotation autour de l'axe \((A,\overrightarrow{{{z}_{1}}})\) avec le chariot \(S_1\). Le bras \(S_3\), auquel on associe le repère \({{R}_{3}}(B,\overrightarrow{{{x}_{3}}},\overrightarrow{{{y}_{3}}},\overrightarrow{{{z}_{3}}})\), est en mouvement de rotation autour de l'axe \((B,\overrightarrow{{{y}_{2}}})\) avec le corps \(S_2\).
Question
Q1. En exprimant que \(S\) roule sans glisser sur \(S_1\) au point \(I_1\), déterminer une relation vectorielle entre \( \overrightarrow { \Omega ({S_1}/R})\) et \(\overrightarrow{ \Omega (S/R})\).
Solution
Il y a R.S.G. au point \(I_1\) donc \(\overrightarrow {V({I_1},S/{S_1})} = \overrightarrow 0\) soit \(\overrightarrow {V({I_1},S/R)} - \overrightarrow {V({I_1},{S_1}/R)} = \overrightarrow 0\) avec
\(\begin{array}{l}\overrightarrow{ V({I_1},S/R)} = \overrightarrow {V(C,S/R)} + \overrightarrow {{I_1}C} \wedge \overrightarrow { \Omega (S/R)}\\\overrightarrow{ V({I_1},S/R)} = \overrightarrow {V(C,S/R) }+ b\overrightarrow x \wedge \overrightarrow{ \Omega (S/R)}\\\overrightarrow{ V({I_1},S/R)} =\overrightarrow {V(C,{S_3}/R)} + b\overrightarrow x \wedge \overrightarrow { \Omega (S/R)}\end{array}\)
et
\(\begin{array}{l}\overrightarrow{ V({I_1},{S_1}/R)} = \overrightarrow{ V({O_1},{S_1}/R) }+ \overrightarrow {{I_1}{O_1}} \wedge \overrightarrow {\Omega ({S_1}/R)}\\\overrightarrow{ V({I_1},S/R)} = (b\overrightarrow x - r\overrightarrow i - \lambda \overrightarrow y) \wedge \overrightarrow {\Omega ({S_1}/R)}\end{array}\)
d'où
\(r\omega \overrightarrow j + b\overrightarrow x \wedge \overrightarrow{ \Omega (S/R)} - (b\overrightarrow x - r\overrightarrow i - \lambda \overrightarrow y) \wedge \overrightarrow{ \Omega ({S_1}/R)} = 0\) car \(\overrightarrow{ V(C,{S_3}/R) }= \overrightarrow { V(C/R) }= {\left[ {\frac{{d\overrightarrow {OC} }}{{dt}}} \right]_R} = r{\left[ {\frac{{d\overrightarrow i}}{{dt}}} \right]_R} = r{\left[ {\frac{{d\overrightarrow i}}{{dt}}} \right]_{S3}} + \overrightarrow { \Omega ({S_3}/R)} \wedge r\overrightarrow i = r\omega \overrightarrow j\)
Question
Q2. En exprimant que \(S\) roule sans glisser sur \(S_2\) au point \(I_2\), déterminer une relation vectorielle entre \( \overrightarrow {\Omega ({S_2}/R)}\) et \(\overrightarrow {\Omega (S/R)}\).
Solution
Il y a R.S.G. au point \(I_2\) donc \(\overrightarrow {V({I_2},S/{S_2})} = \overrightarrow 0\) soit \(\overrightarrow {V({I_2},S/R)} - \overrightarrow {V({I_2},{S_2}/R)} = \overrightarrow 0\) avec
\(\begin{array}{l}\overrightarrow {V({I_2},S/R)} = \overrightarrow {V(C,S/R)} + \overrightarrow {{I_2}C} \wedge \overrightarrow{ \Omega (S/R)}\\\overrightarrow {V({I_2},S/R)} = \overrightarrow {V(C,S/R)} - b\overrightarrow x \wedge \overrightarrow {\Omega (S/R)}\\\overrightarrow {V({I_2},S/R)} = \overrightarrow {V(C,{S_3}/R)} - b\overrightarrow x \wedge \overrightarrow {\Omega (S/R)}\end{array}\)
et
\(\begin{array}{l}\overrightarrow{ V({I_2},{S_2}/R)} = \overrightarrow {V({O_2},{S_2}/R)} + \overrightarrow {{I_2}{O_2}} \wedge \overrightarrow {\Omega ({S_2}/R)}\\\overrightarrow {V({I_2},S/R)} = ( - b\overrightarrow x - r\overrightarrow i + (a - \lambda )\overrightarrow y) \wedge \overrightarrow {\Omega ({S_2}/R)}\end{array}\)
d'où \(r\omega \overrightarrow j - b\overrightarrow x \wedge \overrightarrow{ \Omega (S/R)} - ( - b\overrightarrow x - r\overrightarrow i + (a - \lambda )\overrightarrow y) \wedge \overrightarrow {\Omega ({S_2}/R)} = 0\)
Question
Q3. En déduire que le rapport de variation du mécanisme est : \(\frac{{{\omega _2}}}{{{\omega _1}}} = \frac{\lambda }{{a - \lambda }}\)
Solution
\(\begin{array}{l}r\omega \overrightarrow j + b\overrightarrow x \wedge \overrightarrow{ \Omega (S/R)} - (b\overrightarrow x - r\overrightarrow i - \lambda \overrightarrow y) \wedge {\omega _1}\overrightarrow x = 0\\r\omega \overrightarrow j - b\overrightarrow x \wedge \overrightarrow {\Omega (S/R) }- ( - b\overrightarrow x - r\overrightarrow i + (a - \lambda )\overrightarrow y) \wedge {\omega _2}\overrightarrow x = 0\end{array}\)
donc \(2r\omega \overrightarrow j - r({\omega _1} + {\omega _2})\overrightarrow j - \lambda {\omega _1}\overrightarrow z + (a - \lambda ){\omega _2}\overrightarrow z = 0\)
soit
\(\left\{ {\begin{array}{*{20}{c}}{2r\omega - r({\omega _1} + {\omega _2}) = 0}\\{ - \lambda {\omega _1} + (a - \lambda ){\omega _2} = 0}\end{array}} \right.\)
donc \(\frac{{{\omega _2}}}{{{\omega _1}}} = \frac{\lambda }{{a - \lambda }}\)
Question
Q4. Déterminer \(\overrightarrow {\Omega ({S_3}/R)}\) en relation avec \( {\omega _2}\) et \({\omega _1}\).
Solution
\(\omega = \frac{{{\omega _1} + {\omega _2}}}{2}\)
Question
Q5. Tracer la courbe représentative de ce rapport pour les valeurs \(0 < \lambda < a;\) En pratique \(0 < \frac{{{\omega _2}}}{{{\omega _1}}} < 1,2\). Quelle est alors la valeur maximum de \(\lambda\) ?
Solution
Avec \(a=10\)
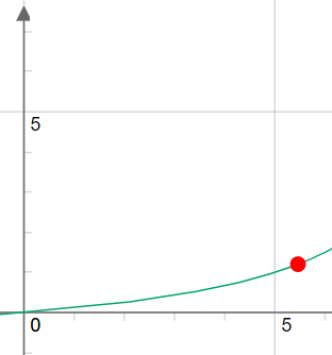
On a alors \(\lambda=\frac{6}{11}a\)