Calcul vectoriel Mécanisme 0
Soit le mécanisme suivant :
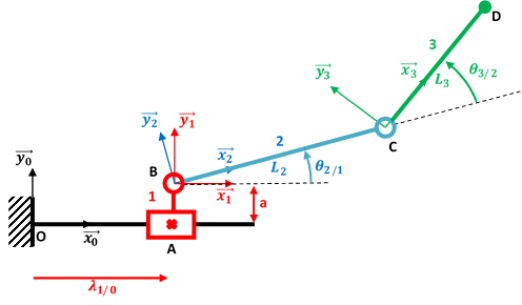
\(\overrightarrow{OA}={{\lambda }_{1/0}}\overrightarrow{{{x}_{0}}}~~~~~;~~~~~\overrightarrow{AB}=a\overrightarrow{{{y}_{0}}}=a\overrightarrow{{{y}_{1}}}~~~~~;~~~~~\overrightarrow{BC}={{L}_{2}}\overrightarrow{{{x}_{2}}}~~~~~;~~~~~\overrightarrow{CD}={{L}_{3}}\overrightarrow{{{x}_{3}}}\)
\({{\mathfrak{B}}_{i}}\left( \overrightarrow{{{x}_{i}}},\overrightarrow{{{y}_{i}}},\overrightarrow{{{z}_{i}}} \right)~,i=\left( 1,2,3 \right)\) sont des bases orthonormées directes telles que \(\forall \left( i,j \right)\overrightarrow{{{z}_{i}}}=\overrightarrow{{{z}_{j}}}\)
Dans tout l'exercice, on n'utilisera que le paramétrage qui est donné, en particulier concernant les angles.
Question
Q1. Exprimer le vecteur \(\overrightarrow{OD}\) en fonction des données.
Solution
\(\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}\)
\(\overrightarrow{OD}={{\lambda }_{1/0}}\overrightarrow{{{x}_{0}}}+a\overrightarrow{{{y}_{0}}}+{{L}_{2}}\overrightarrow{{{x}_{2}}}+{{L}_{3}}\overrightarrow{{{x}_{3}}}\)
Question
Q2. Exprimer les vecteurs \(\left( \overrightarrow{{{x}_{i}}},\overrightarrow{{{y}_{i}}} \right),~i=\left( 1,2,3 \right)\) dans la base \(0\) et faire les figures de changement de bases associées.
Solution
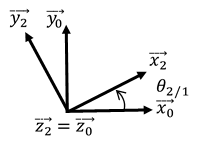
\(\overrightarrow{{{x}_{1}}}=\overrightarrow{{{x}_{0}}}~~~~~;~~~~~\overrightarrow{{{y}_{1}}}=\overrightarrow{{{y}_{0}}}\)
\({{\theta }_{1/0}}=0\)
\(\overrightarrow{{{x}_{2}}}=\cos {{\theta }_{2/1}}\overrightarrow{{{x}_{0}}}+\sin {{\theta }_{2/1}}\overrightarrow{{{y}_{0}}}\)
\(\overrightarrow{{{y}_{2}}}=-\sin {{\theta }_{2/1}}\overrightarrow{{{x}_{0}}}+\cos {{\theta }_{2/1}}\overrightarrow{{{y}_{0}}}\)
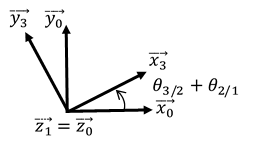
\(\overrightarrow{{{x}_{3}}}=\cos \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)\overrightarrow{{{x}_{0}}}+\sin \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)\overrightarrow{{{y}_{0}}}\)
\(\overrightarrow{{{y}_{3}}}=-\sin \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)\overrightarrow{{{x}_{0}}}+\cos \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)\overrightarrow{{{y}_{0}}}\)
Question
Q3. En déduire l'expression de \(\overrightarrow{OD}\) dans la base \(0\).
Solution
\(\overrightarrow{OD}={{\lambda }_{1/0}}\overrightarrow{{{x}_{0}}}+a\overrightarrow{{{y}_{0}}}+{{L}_{2}}\overrightarrow{{{x}_{2}}}+{{L}_{3}}\overrightarrow{{{x}_{3}}}\)
\(\overrightarrow{OD}={{\lambda }_{1/0}}\overrightarrow{{{x}_{0}}}+a\overrightarrow{{{y}_{0}}}+{{L}_{2}}\left( \cos {{\theta }_{2/1}}\overrightarrow{{{x}_{0}}}+\sin {{\theta }_{2/1}}\overrightarrow{{{y}_{0}}} \right)+{{L}_{3}}\left( \cos {{\theta }_{3/0}}\overrightarrow{{{x}_{0}}}+\sin {{\theta }_{3/0}}\overrightarrow{{{y}_{0}}} \right)\)
\(\overrightarrow{OD}=\left( {{\lambda }_{1/0}}+{{L}_{2}}\cos {{\theta }_{2/1}}+{{L}_{3}}\cos {{\theta }_{3/0}} \right)\overrightarrow{{{x}_{0}}}+\left( a+{{L}_{2}}\sin {{\theta }_{2/1}}+{{L}_{3}}\sin {{\theta }_{3/0}} \right)\overrightarrow{{{y}_{0}}}\)
Question
Q4. Exprimer le vecteur \(\overrightarrow{BC}\) dans les différentes bases du système.
Solution
\(\overrightarrow{BC}={{L}_{2}}\overrightarrow{{{x}_{2}}}\)
\(\overrightarrow{BC}={{L}_{2}}\left( \cos {{\theta }_{2/1}}\overrightarrow{{{x}_{0}}}+\sin {{\theta }_{2/1}}\overrightarrow{{{y}_{0}}} \right)\)
\(\overrightarrow{BC}={{L}_{2}}\left( \cos {{\theta }_{2/1}}\overrightarrow{{{x}_{1}}}+\sin {{\theta }_{2/1}}\overrightarrow{{{y}_{1}}} \right)\)
\(\overrightarrow{BC}={{L}_{2}}\left( \cos {{\theta }_{3/2}}\overrightarrow{{{x}_{3}}}-\sin {{\theta }_{3/2}}\overrightarrow{{{y}_{3}}} \right)\)
Question
Q5. Exprimer l'angle orienté \(\widehat{\left( \overrightarrow{{{y}_{0}}},\overrightarrow{{{x}_{3}}} \right)}\)
Solution
\(\widehat{\left( \overrightarrow{AB},\overrightarrow{CD} \right)}=\widehat{\left( \overrightarrow{{{y}_{0}}},\overrightarrow{{{x}_{3}}} \right)}=\widehat{\left( \overrightarrow{{{y}_{0}}},\overrightarrow{{{x}_{0}}} \right)}+\widehat{\left( \overrightarrow{{{x}_{0}}},\overrightarrow{{{x}_{1}}} \right)}+\widehat{\left( \overrightarrow{{{x}_{1}}},\overrightarrow{{{x}_{2}}} \right)}+\widehat{\left( \overrightarrow{{{x}_{2}}},\overrightarrow{{{x}_{3}}} \right)}=\left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)-\frac{\pi }{2}\)
Question
Q6. Calculer le produit scalaire \(\overrightarrow{AB}.\overrightarrow{CD}\) par la définition
Solution
\(\overrightarrow{AB}.\overrightarrow{CD}=a\overrightarrow{{{x}_{0}}}.{{L}_{3}}\overrightarrow{{{x}_{3}}}=~a{{L}_{3}}\overrightarrow{{{x}_{0}}}.\overrightarrow{{{x}_{3}}}\)
\(\overrightarrow{{{x}_{0}}}.\overrightarrow{{{x}_{3}}}=\overrightarrow{{{x}_{0}}}\overrightarrow{{{x}_{3}}}\cos \widehat{\left( \overrightarrow{{{x}_{0}}},\overrightarrow{{{x}_{3}}} \right)}=\cos \widehat{\left( \overrightarrow{{{x}_{0}}},\overrightarrow{{{x}_{3}}} \right)}=\cos \left( \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)-\frac{\pi }{2} \right)=\sin \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)\)
\(\overrightarrow{AB}.\overrightarrow{CD}=a{{L}_{3}}\sin \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)\)
Question
Q7. Calculer le produit vectoriel \(\overrightarrow{AB}\wedge\overrightarrow{CD}\) par la définition
Solution
\(\overrightarrow{AB}\wedge\overrightarrow{CD}=a\overrightarrow{{{x}_{0}}}\wedge{{L}_{3}}\overrightarrow{{{x}_{3}}}=~a{{L}_{3}}\overrightarrow{{{x}_{0}}}\wedge\overrightarrow{{{x}_{3}}}\)
\(\overrightarrow{{{x}_{0}}}\wedge\overrightarrow{{{x}_{3}}}=\overrightarrow{{{x}_{0}}}\overrightarrow{{{x}_{3}}}\sin \widehat{\left( \overrightarrow{{{x}_{0}}},\overrightarrow{{{x}_{3}}} \right)}\overrightarrow{{{z}_{0}}}=\sin \widehat{\left( \overrightarrow{{{x}_{0}}},\overrightarrow{{{x}_{3}}} \right)}\overrightarrow{{{z}_{0}}}=\sin \left( \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)-\frac{\pi }{2} \right)\overrightarrow{{{z}_{0}}}=-\cos \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)\overrightarrow{{{z}_{0}}}\)
\(\overrightarrow{AB}\wedge\overrightarrow{CD}=-~a{{L}_{3}}\cos \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)\overrightarrow{{{z}_{0}}}\)
Question
Q8. Exprimer \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) en notation verticale
Solution
\(\overrightarrow{AB}={{\left( \begin{matrix} 0 \\ a \\ 0 \\ \end{matrix} \right)}^{{{\mathfrak{B}}_{0}}}}\)
\(\overrightarrow{CD}={{\left( \begin{matrix} {{L}_{3}} \\ 0 \\ 0 \\ \end{matrix} \right)}^{{{\mathfrak{B}}_{3}}}}={{\left( \begin{matrix} {{L}_{3}}\cos \left( +{{\theta }_{2/1}} \right) \\ {{L}_{3}}\sin \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right) \\ 0 \\ \end{matrix} \right)}^{{{\mathfrak{B}}_{0}}}}\)
Question
Q9. Calculer le produit scalaire \(\overrightarrow{AB}.\overrightarrow{CD}\) en notation verticale
Solution
\(\overrightarrow{AB}.\overrightarrow{CD}={{\left( \begin{matrix} 0 \\ a \\ 0 \\ \end{matrix} \right)}^{{{\mathfrak{B}}_{0}}}}.{{\left( \begin{matrix} {{L}_{3}}\cos \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right) \\ {{L}_{3}}\sin \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right) \\ 0 \\ \end{matrix} \right)}^{{{\mathfrak{B}}_{0}}}}=a{{L}_{3}}\sin \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)\).
Question
Q10. Calculer le produit vectoriel \(\overrightarrow{AB}\wedge\overrightarrow{CD}\) en notation verticale.
Solution
\(\overrightarrow{AB}\wedge\overrightarrow{CD}={{\left( \begin{matrix} 0 \\ a \\ 0 \\ \end{matrix} \right)}^{{{\mathfrak{B}}_{0}}}}\wedge{{\left( \begin{matrix} {{L}_{3}}\cos \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right) \\ {{L}_{3}}\sin \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right) \\ 0 \\ \end{matrix} \right)}^{{{\mathfrak{B}}_{0}}}}={{\left( \begin{matrix} 0 \\ 0 \\ -a{{L}_{3}}\cos \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right) \\ \end{matrix} \right)}^{{{\mathfrak{B}}_{0}}}}\)
\(\overrightarrow{AB}\wedge\overrightarrow{CD}=-a{{L}_{3}}\cos \left( {{\theta }_{3/2}}+{{\theta }_{2/1}} \right)\overrightarrow{{{z}_{0}}}\)