Changement de base v1
On définit les trois repères suivants : \({{R}_{1}}({{O}_{1}},\overrightarrow{{{i}_{1}}},\overrightarrow{{{j}_{1}}},\overrightarrow{{{k}_{1}}})\) \({{R}_{2}}({{O}_{2}},\overrightarrow{{{i}_{2}}},\overrightarrow{{{j}_{2}}},\overrightarrow{{{k}_{2}}})\) \({{R}_{3}}({{O}_{3}},\overrightarrow{{{i}_{3}}},\overrightarrow{{{j}_{3}}},\overrightarrow{{{k}_{3}}})\).
• Où les \(\overrightarrow{{{i}_{m}}},\overrightarrow{{{j}_{m}}},\overrightarrow{{{k}_{m}}}\) sont les vecteurs unitaires formant les bases des \({{R}_{m}}\).
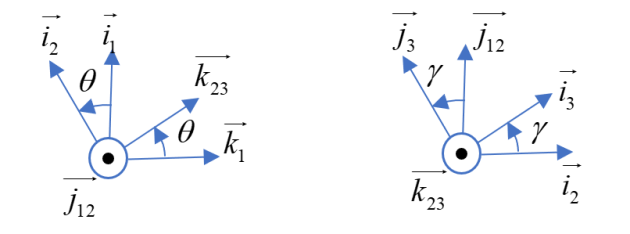
• On passe de R1 à R2 par une rotation \(\theta \) autour de l'axe défini par \(({{O}_{1}},\overrightarrow{{{j}_{1}}})\).
• On passe de R2 à R3 par une rotation \(\gamma \) autour de l'axe défini par \(({{O}_{2}},\overrightarrow{{{k}_{2}}})\).
Question
Q1. Faire les figures de changement de base.
Question
Q2. Donner les résultats des opérations suivantes :
1. \(\overrightarrow{{{i}_{3}}}\cdot \overrightarrow{{{i}_{2}}},\overrightarrow{{{i}_{3}}}\cdot \overrightarrow{{{j}_{2}}},\overrightarrow{{{j}_{2}}}\cdot \overrightarrow{{{j}_{3}}},\overrightarrow{{{i}_{2}}}\cdot \overrightarrow{{{j}_{3}}}\)
2. \(\overrightarrow{{{i}_{3}}}\wedge \overrightarrow{{{i}_{2}}},\overrightarrow{{{i}_{3}}}\wedge \overrightarrow{{{j}_{2}}},\overrightarrow{{{j}_{2}}}\wedge \overrightarrow{{{j}_{3}}},\overrightarrow{{{i}_{2}}}\wedge \overrightarrow{{{j}_{3}}}\)
3. \(\overrightarrow{{{i}_{3}}}\cdot {{\overrightarrow{{{k}_{1}}}}_{{}}}\)
et \(\overrightarrow{{{i}_{3}}}\wedge \overrightarrow{{{j}_{1}}}\)
Solution
 Les calculs écrits si dessous sont les seuls à réaliser ! ! ! Si vous avez des lignes de calculs en plus pour attendre le résultat VOYEZ votre enseignant.
Les calculs écrits si dessous sont les seuls à réaliser ! ! ! Si vous avez des lignes de calculs en plus pour attendre le résultat VOYEZ votre enseignant.
1. \(\overrightarrow{{{i}_{3}}}\cdot \overrightarrow{{{i}_{2}}}=cos\gamma\)
\(\overrightarrow{{{i}_{3}}}\cdot \overrightarrow{{{j}_{2}}}=sin\gamma\)
\(\overrightarrow{{{j}_{2}}}\cdot \overrightarrow{{{j}_{3}}}=cos\gamma\)
\(\overrightarrow{{{i}_{2}}}\cdot \overrightarrow{{{j}_{3}}}=-sin\gamma\)
2. \(\overrightarrow{{{i}_{3}}}\wedge \overrightarrow{{{i}_{2}}}=-sin\gamma\overrightarrow{k_{23}}\)
\(\overrightarrow{{{i}_{3}}}\wedge \overrightarrow{{{j}_{2}}}=cos\gamma\overrightarrow{k_{23}}\)
\(\overrightarrow{{{j}_{2}}}\wedge \overrightarrow{{{j}_{3}}}=sin\gamma\overrightarrow{k_{23}}\)
\(\overrightarrow{{{i}_{2}}}\wedge \overrightarrow{{{j}_{3}}}=cos\gamma\overrightarrow{k_{23}}\)
3. \(\overrightarrow{{{i}_{3}}}\cdot {{\overrightarrow{{{k}_{1}}}}_{{}}}=-cos\gamma.sin\theta\)
et\( \overrightarrow{{{i}_{3}}}\wedge \overrightarrow{{{k}_{1}}}=\overrightarrow{{{i}_{3}}}\wedge [cos\theta.\overrightarrow{{{k}_{23}}}-sin\theta.\overrightarrow{{{i}_{2}}}]==-cos\theta.\overrightarrow{{{j}_{3}}}+cos\gamma.sin\theta.\overrightarrow{{{k}_{23}}}\)
Question
Q3. Calculer : \({{\left( \overrightarrow{{{j}_{3}}}\wedge \overrightarrow{{{k}_{1}}} \right)} ~\boldsymbol{\cdot }~ }\overrightarrow{{{j}_{2}}}\)
Solution
\({{\left( \overrightarrow{{{j}_{3}}}\wedge \overrightarrow{{{k}_{1}}} \right)} ~\boldsymbol{\cdot }~ }\overrightarrow{{{j}_{2}}}={{\left( \overrightarrow{{{j}_{12}}}\wedge \overrightarrow{{{j}_{3}}} \right)} ~\boldsymbol{\cdot }~ }\overrightarrow{{{k}_{1}}}={{\left( \overrightarrow{{{k}_{1}}}\wedge \overrightarrow{{{j}_{12}}} \right)} ~\boldsymbol{\cdot }~ }\overrightarrow{{{j}_{3}}}=-\overrightarrow{{{i}_{1}}}\cdot {{\overrightarrow{{{j}_{3}}}}_{{}}}=cos\theta.sin\gamma\)
Question
Q4. Calculer : \({{\left( \frac{d\overrightarrow{{{i}_{2}}}}{dt} \right)}_{R1}} et ~~{{\left( \frac{d\overrightarrow{{{j}_{3}}}}{dt} \right)}_{R1}}\)
Solution
\({{\left( \frac{d\overrightarrow{{{i}_{2}}}}{dt} \right)}_{R1}}={{\left( \frac{d\overrightarrow{{{i}_{2}}}}{dt} \right)}_{R2}}+\overrightarrow{\Omega_{2/1}}\wedge\overrightarrow{i_{2}}=\dot{\theta{}}\overrightarrow{j}_{12}\wedge\overrightarrow{{{i}_{2}}}=-\dot{\theta{}}\overrightarrow{k}_{23}\)
\({{\left( \frac{d\overrightarrow{{{j}_{3}}}}{dt} \right)}_{R1}}={{\left( \frac{d\overrightarrow{{{j}_{3}}}}{dt} \right)}_{R3}}+\overrightarrow{\Omega_{3/1}}\wedge\overrightarrow{j_{3}}=[\dot{\theta{}}\overrightarrow{j}_{12}+\dot{\gamma}\overrightarrow{k}_{23}]\wedge\overrightarrow{{{j}_{3}}}=\dot{\theta{}}sin\gamma\overrightarrow{k}_{23}-\dot{\gamma}\overrightarrow{i}_{3}\)