This story also appears in the Additional Resources section of Maths300 Lesson 97, Tackling Times Tables. The software and all activities in this lesson are focused on skill development (ie: automatic times tables response) in conjunction with cementing an understanding of the multiplication concept. Poly Plug is the preferred demonstration lesson throughout the lesson and this is also reflected in the software. I was weeding the vegie patch recently when Jesse, my new Year 5 neighbour, perched on the fence and engaged me in conversation. We had lived in this house less than three months, and, although I had known Jesse previously, we had much to explore of each other now we were neighbours. The conversation drifted around to: What do you do Doug? Hmmm, well I try to help teachers improve the way they teach mathematics. Mathematics. I'm bad at that. (Then in the same breath.) Well, not bad exactly, but I don't know my tables. … Well, I need to learn my sixes and sevens and eights.Always willing to be a teacher, I explained to Jesse how she could use her calculator to help learn them. Suppose you want to learn 6 x 7. Just press those buttons on the calculator, BUT don't press equals. Before you press = you must think about 6 x 7 in your head and guess what the calculator will show after you press equals. Then, when you press = the calculator will correct you.Jesse said she would try that. I moved on - pedagogically speaking. That is one of the activities that will help you remember what to say when you are asked 6 x 7, but what does six times seven mean? Huh? Like, if I asked you to put a picture of six times seven in your head, what would you see? A 6 and a cross and a 7.Uh oh, I began to perceive a problem here. Well they are the symbols for six times seven, but do you know what they mean? Not really, what do you mean?Now it is not I, rather my Princess, who plants the vegies - you already know my job - and in this case she clearly hadn't thought ahead. There was nothing in the garden arranged in six rows of seven. The best I could call on was the spring onions. You see those spring onions there … (quizzical look) … the ones with the pointy stems a bit like spears. Yes. How have they been planted?Straddling the ubiquitous neighbourhood fence, Jesse had a good view of their layout. In four rows of four. So, when Ina planted them she planted four in a row. Yes. And how many times did she do that? Four. So, the spring onions make a picture of 4 x 4. What would be the picture be for 6 x 7? Ahh (thinking) … six rows with seven. That's right. Now keep that picture in your head, think of spring onions in that layout if you like, and imagine yourself moving around to look at the garden bed from the side. What is the picture now? Seven rows with six in them. Well done. So, now when you have to think about a times table, like when you are using the calculator to help you learn, you can picture what it means.We checked the image for a couple of other times tables; you know the sort of question, "What do you see for 6 x 4?" and so on, but it was probably a good thing Jesse was called in for tea, because I was about to start on: I'll think of a number. You tell me all the ways you could arrange it in rows, and then tell me the times tables for each one.When I was called for tea too, I acted out this little cameo again with Ina, who is substantially beyond Year 5. She thought Jesse was quite reasonable thinking of six sevens as a six and a cross and a seven. When pressed for an image, Ina saw six scattered collections of seven. That increased my admiration for the order in our vegetable garden, but it did concern me that both she and Jesse have come their respective distances through maths education and don't realise that all multiplication can be pictured as counting in a rectangle. Why do we line kids up to count them onto buses on excursions? It's easier to do the counting, right? Right. Counting can be done if the objects are all over the place, but it is easier to order them first. It's the same with multiplication (and its backwards form, division). Multiplication is counting the count:
Think of those spring onions again:
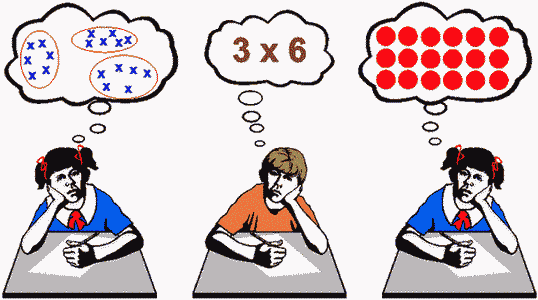
If a Year 5 student, who would be described by all her teachers as bright, enthusiastic and capable, has not developed a picture of multiplication are we doing our kids a disservice?
create brain pictures on which to hang their mathematical understandings.
Whose brain picture is more powerful?
|