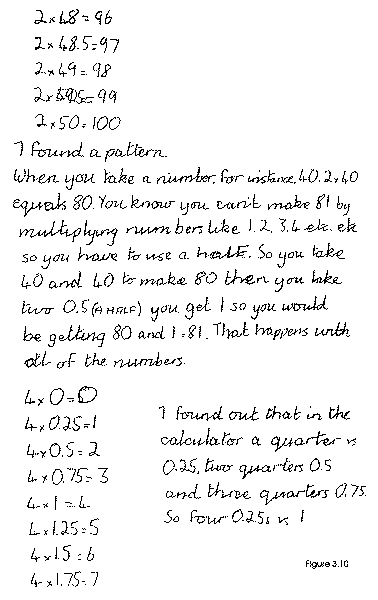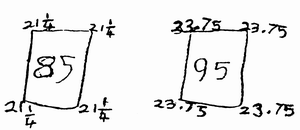|
Decimals & Fractions
 |
When the calculator is used freely as a core resource in challenging investigative activities children meet decimals quite early. How do they interpret them and what can teachers do to support their learning? This article from pages 18 - 23 of the CAN Report contains several classroom vignettes that support teachers in tackling this challenge.
As soon as they start to use the division key on the calculator, children see decimal numbers in the display. At the end of the first year of CAN, the evaluator, after a visit to a project classroom, wrote about an incident in which a six-year-old girl had consulted her.
Figure 3.9, Page 19 CAN Report
Calculating Changes investigations sheets similar to this can be found at the end of the article.
|
A girl brought me a calculator displaying 3·125. 'Do you know numbers like this?' she asked. When I said I did, she showed me what she had been doing. 'We are doing things about fifty,' she said, 'but I thought I would like to halve it.' She showed me 25, halved again and showed me 12·5, halved again to produce 6·25, and finally obtained 3·125.
I suggested that halving was like sharing things between us, so we shared 25 cubes between us. She gave us 12 each, but she couldn't halve the one left over. 'Let's make a Plasticine cube and then we can cut it in half..' I said. 'How many have we got?' 'Twelve and a half,' she replied. Then I invited her to try it on the calculator. 'Is that how the calculator writes a half?' she asked.
We went on to make six and a quarter, using the Plasticine and consulting the calculator. She accepted that the calculator wrote six and quarter as 6·25. She insisted on going on: 'So that's how the calculator writes three and an eighth.' She commented that the numbers were getting longer, but her confidence in matching the Plasticine with the calculator display seemed undaunted.
Similar experiences occurred in many classrooms, and many children came to know that '0·5 is the way the calculator writes a half'. For example, a teacher asked Nigel, a low-attaining eight-year-old, to explore patterns of dividing by two, initially without a calculator. She started him off with the sequence 10 ÷ 2 = 5, 12 ÷ 2 = 6, 14 ÷ 2 = 7. Nigel continued, using the calculator, and recorded:
15 ÷ 2 = 7·5, 16 ÷ 2 = 8, 17 ÷ 2 = 8·5.
The teacher asked him to predict the answer to 23 ÷ 2, which he did correctly and confidently.
For many children, a stream of figures after the decimal point is at first a great surprise. An advisory teacher interviewed Gail, another low-attaining eight-year-old, and part of their conversation went as follows:
| Teacher: |
Can you share 16 sweets between three people? |
| Gail: |
They will all get five and there will be one left over. |
| Teacher: |
Do you ever use the calculator for sharing? Show me.
[Gail put in 16 ÷ 3 and got 5·3333333.] |
| Teacher: |
What does it mean? |
| Gail: |
I think it's wrong. |
Later, Gail explained to the advisory teacher, in response to 13 ÷ 2 = 6·5: 'That's how much they get. The point five is the bit left over.'
Some teachers have devised activities which ensure that children meet decimals. One activity was a workcard which started a pattern (Figure 3.9). Children investigated the pattern in different ways. David used Unifix.
| David: |
Two lots of three - that's six. That's too many ... I want five. Two lots of two is four. It must be two and a half. |
| Teacher: |
Can you check that on the calculator?
[David keyed in 2 x 2·5 = ]
|
Some children extended the pattern to much larger numbers, and some explored three times and four times. Figure 3.10 shows part of a child's work on this activity.
|
Figure 3.10, Page 20 CAN Report
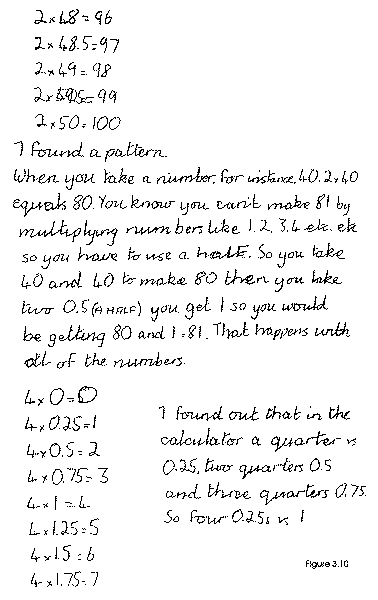
|
A teacher asked a group of first-year junior children (aged seven to eight): 'How could we show fractions on a calculator?' None of them knew, so she took an example, and wrote down the fraction 1/4 . She said:'The way we write it - it contains the numbers one and four. What can you do with one and four on the calculator?' Gus recorded what he could do in a very systematic way; he wrote:
4 + 1 = 5
4 x 1 = 4
4 - 1 = 3
4 ÷ 1 = 4
|
1 + 4 = 5
1 x 4 = 4
1 - 4 = -3
1 ÷ 4 = 0·25
|
Then he said: 'I think a quarter is 0·25.' And he checked it in two ways:
0·25 + 0·25 + 0·25 + 0·25 = 1
0·25 x 4 = 1
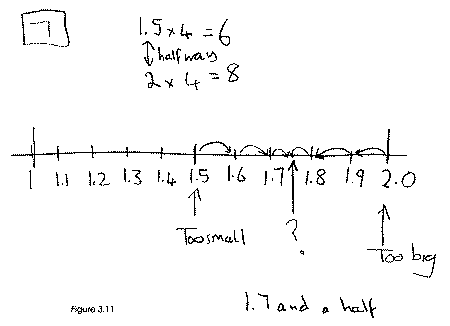
The child's work shown in Figure 3.11 is the familiar activity of putting a number in the middle of a square, and then putting a number at each of the four corners, these four numbers adding up to the number in the middle. (Ed: see Number Shapes & Box Hunt.) The child's sketch may not be very accurate, but it shows clear appreciation that 1·5 is half way between 1 and 2 , and that 1·75 is halfway between 1·5 and 2.
|
| One teacher gives an extended account of work on decimals done by a group of eight to nine year olds:
One group became very interested in the remainders in division, and on their calculator checks. They had:
43 ÷ 2 = 21 rem 1 ... Check: 21·5
41 ÷ 3 = 13 rem 2 ... Check: 13·666666
I asked them about 40 ÷ 3. That was easy: 13 rem 1. On the calculator? 'Thirteen point something.' They did the following calculations mentally and checked them on the calculator:
40 ÷ 3 = 13 rem 1 ... Check: 13·333333
39 ÷ 3 = 13 rem 0 ... Check: 13
38 ÷ 3 = 12 rem 2 ... Check: 12·666666
|
Figure 3.11, Page 21 CAN Report
|
They were able to predict the next calculation:
37 ÷ 3 = 12 rem 1 ... Check: 12·333333
and they continued the pattern down to 27 ÷ 3 = 9.
I returned and asked: 'Why ·333333 and ·666666?' They were not sure. We recalled:
49 ÷ 2 = 24 rem 1 ... Check: 24·5
They said that point five is half, and remainder one when dividing by two is a half. One of them then suggested that ·333333 was three quarters. 'No,' the other one said. 'Point seven five is three quarters and point two five is one quarter.'
So we got out the fraction cakes and shared them between three people. they realised that 4 ÷ 3 = 1 rem 1, and in dividing by three, remainder one is one third. We returned to the calculator. and recorded:
40 ÷ 3 = 13 rem 1 ... Check: 13·333333
The children said: '·333333 is one out of three, or a third.'
41 ÷ 3 = 13 rem 2 ... Check: 13·666666
The children said: '·666666 is two out of three, or two thirds.'
Many children have built up a good deal of knowledge of the decimal equivalents of familiar fractions, but the calculator does not make it plain why it writes fractions in these ways. This is a much more difficult task.
Ways of developing this idea include working with sums of money such as £0·50, £0·25, £0·33. Children also need to explore ways in which the calculator writes fractions such as 1/10 and 1/100 , and relate this to their understanding of place value for whole numbers.
The following conversation between a teacher and two nine-year-old children shows the children's developing awareness of why the calculator writes fractions as it does. They were again doing the familiar activity of putting a number in a box, and writing numbers at the corners (Figure 3.12).

Figure 3.12, Page 22 CAN Report
The teacher asked Michael and Richard to explain:
| Teacher: |
Can you tell us what you've done Michael? |
| Michael: |
Nought point two five, and you add them all together and you get one.
|
| Teacher: |
You seem to know that. ... How do you know that? |
| Michael: |
Put one ... divide by four.
|
| Richard: |
'Cos ... point two five is a quarter ... I was just playing around with the calculator ... when I was in the infants ... I just found it out. |
| Teacher: |
But how do you know it is a quarter? ... What if someone didn't believe you? How could you prove it to them?
|
| Michael: |
Because 25 is a quarter of 100, and if you add a nought on the beginning, it would be a quarter of one as well. |
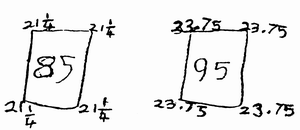
Figure 3.13, Page 22 CAN Report
|
Carole, working on the same activity, sometimes recorded in decimals and sometimes in fractions (Figure 3.13).
The decimal equivalent of one third shows a further complication. The calculator gives:
1 ÷ 3 = 0·3333333
but on most four-function calculators:
0·333333 x 3 = 0·9999999
|
However all children will have to tackle this rounding problem in the mathematics National Curriculum:
Know how to interpret results on a calculator which has rounding errors.
Example: Interpret 7 ÷ 3 x 3 = 6·9999999 if it occurs on a calculator. [AT 4, Level 4]
In fact, as children explore numbers with their calculators, they become more familiar with the structure of the number system than they could in any other way at this age. Their developing knowledge includes not only whole numbers, positive and negative, but also decimal numbers.
Most children in the project have not yet reached a full understanding of decimals, although they can use them in many situations, as can be seen from the examples above. The mistakes in James' work, shown in Figure 3.14, indicate what is lacking in his understanding of decimal place value. He makes a consistent error whenever he has to add or subtract a number with one decimal place from a number with two decimal places; he treats the decimal parts as if they were whole numbers. If he were urged to check with the calculator, this would cause a conflict between what he thought and what the calculator showed. this might lead him to further exploration and to developing his understanding.

Figure 3.14, Page 23 CAN Report
This Calculating Changes assessment activity is based on James' work.
In order to help children to make sense of the number system, teachers need to develop a new teaching skill. Children find out from their calculators how numbers behave, but the calculator does not show why numbers behave like this. The teachers must devise activities which enable children to make sense of what they have found out from the calculator.
In the past, teachers have been able to keep negative numbers and decimals hidden from children until they thought the children would understand a full explanation. This is no longer a possible strategy; children cannot be prevented from discovering negative numbers and decimals for themselves on the calculator display at an early age. Dealing with this situation makes new demands on the teacher. Negative numbers seem to have caused few problems, but decimals are conceptually much more difficult.
Investigation Sheets
Based on the C.A.N. work above, these sheets have been produced by Calculating Changes members to encourage children to 'run into' decimal numbers.

Return to C.A.N. Report Index
Calculating Changes ... is a division of ... Mathematics Centre
|