Leçon: Bases de statistiques et probabilités¶
Paquets utiles¶
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import math
import scipy
import scipy.stats as stats
/home/nico/.pyenv/versions/miniconda3-latest/lib/python3.9/site-packages/scipy/__init__.py:146: UserWarning: A NumPy version >=1.16.5 and <1.23.0 is required for this version of SciPy (detected version 1.23.1
warnings.warn(f"A NumPy version >={np_minversion} and <{np_maxversion}"
Statistiques¶
Définition¶
D'après wikipédia:
Statistics is the discipline that concerns the collection, organization, displaying, analysis, interpretation and presentation of data.
C'est un outil mathématique très puissant qui permet de:
- comprendre et résumer des données (indicateurs univariés, méthodes multi-variées, ...)
- valider des hypothèses (par des tests statistiques)
- modéliser des données (régression) ou identifier des patterns (clustering, ...)
- mesurer une incertitude (intervalle de confiance, ...)
- ...
Statistiques descriptives¶
Toutes les données que vous allez analyser sont des échantillons !!!¶
En statistiques, on considère que chaque échantillon est tiré au hasard à partir d'une population. Cela implique qu'un échantillon mesure une valeur entachée d'erreur de la vraie valeur de la population
Les différents tirages possibles donnent lieu à des échantillons qui varient: on parle de fluctuation d'échantillonnage
Notion de variable aléatoire¶
En statistique, on travaille généralement sur des variables dont on ne connait pas les vraies valeurs (ex: la taille de la population francaise), c'est pourquoi on les modélise souvent comme des variables aléatoires
Notion d'estimateur statistique¶
Du fait des fluctuations d'échantillonnage on ne connait généralement pas la vraie valeur (celle de l'ensemble de la populatation) des indicateurs que l'on souhaite calcule, mais plutôt de valeurs estimées (dont on peut mesurer l'erreur)
C'est pour cela qu'on parle d'estimateurs !
Répartition d'une variable¶
histogramme de repartition vs distribution théorique¶
male_df = pd.DataFrame([140, 145, 160, 190, 155, 165, 150, 190, 195, 138, 160, 155, 153, 145, 170, 175, 175, 170, 180, 135, 170, 157, 130, 185, 190, 155, 170, 155, 215, 150, 145, 155, 155, 150, 155, 150, 180, 160, 135, 160, 130, 155, 150, 148, 155, 150, 140, 180, 190, 145, 150, 164, 140, 142, 136, 123, 155],
columns=['weight'])
male_df['sex'] = 'male'
female_df = pd.DataFrame([140, 120, 130, 138, 121, 116, 125, 145, 150, 112, 125, 130, 120, 130, 131, 120, 118, 125, 135, 125, 118, 122, 115, 102, 115, 150, 110, 116, 108, 95, 125, 133, 110, 150, 108],
columns=['weight'])
female_df['sex'] = 'female'
weights_df = pd.concat([male_df, female_df], ignore_index=True)
weights_df.sample(5)
| weight | sex | |
|---|---|---|
| 78 | 122 | female |
| 35 | 150 | male |
| 14 | 170 | male |
| 64 | 145 | female |
| 53 | 142 | male |
ax = sns.histplot(weights_df["weight"], bins=len(weights_df))
ax.set_xlabel("Weight (in lbs)")
ax.set_title("Distribution of weight variable")
plt.show()
En réduisant le nombre de bins, on obtient un histogramme différent
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 4))
ax1.hist(weights_df["weight"], bins=12)
ax1.set_xlabel("weight")
ax1.set_title("Simple distribution of weight")
ax2 = sns.histplot(weights_df["weight"], bins=12, ax=ax2, kde=True)
ax2.set_title("Density estimation of weight")
plt.show()
La courbe bleue cherche à estimer la distribution théorique de notre variable poids
Estimateurs statistiques univariés¶
Mesures de tendence centrale¶
Moyenne (moment d'ordre 1)¶
La moyenne de la population des $N$ élements, s'écrit:
La moyenne des $n$ (n<N) échantillons, s'écrit:
Dans le cas de notre dataset :
np.mean(weights_df.weight)
145.15217391304347
Mediane¶
Il s'agit de la valeur qui partage une série croissante en deux "parties" de même taille : 50% des données sont contenues dans chaque "partie"
Exemple pour les séries impaires : 1 2 2 5 7 8 9
Pour les séries paires, on fait la moyenne des deux valeurs au milieu : 1 2 2 5 7 8 9 12
la médiane dans ce cas est $\frac{5+7}{2} = 6$
Dans le cas de notre dataset :
np.median(weights_df.weight)
145.0
Moyenne vs mediane¶
En général, les valeurs de la médiane et de la moyenne d'une série seront différente !
Elle seront identique lorsque la distribution sera parfaitement symétrique
La moyenne est sensible aux valeurs extrêmes alors que la médiane y est robuste !!!
---> Prvilégiez la médiane lorsque vos data set contient des valeurs extrêmes
Les quantiles¶
Il s'agit de la généralisation de l'idée de la médiane: on veut faire des "paquets" de données ayant la même taille
On peut découper notre série en différents paquets $q$ :
- pour $q = 4$ on parle de quartile
- pour $q = 10$ on parle de décile
- pour $q = 100$ on parle de percentile
- ...
Plus généralement, $q$ est le quantile d'ordre q
On représente souvent les quartiles d'une série par une boite à moustache (boxplot)
avec matplotlib¶
plt.boxplot(weights_df.weight)
plt.title("Box plot of weight")
plt.show()
avec seaborn¶
ax = sns.boxplot(x=weights_df["weight"])
Ou par un violin plot, qui permet de représenter la densité des points:
ax = sns.violinplot(x=weights_df["weight"])
Intervalle Inter Quartile (Inter Quartile Range)¶
Il s'agit d'une mesure de dispersion simple: $IIQ = Q3 - Q1$
Elle correspond à la taille de la boite dans un boxplot
Le critère de fisher est souvent utilisé pour détecter les valeurs abérantes (outliers) dans un boxplot: les moustaches sont positionnées à une distance de $1.5*IIQ$ au dela des moustaches.
On considère alors les variables en dehors des moustaches comme des valeurs abérantes
Mode¶
Il s'agit de la valeur la plus fréquente d'une série
1 3 5 6 6 6 7 7 12 12 17
Le mode de cette série est 6
1 3 5 6 6 6 7 7 12 12 12 17
Cette série est bi-modale : elle a pour mode 6 et 12
Mesure de dispersion: moments d'ordre supérieur (k>1)¶
la variance : moment d'ordre 2¶
La variance est une mesure de dispersion de votre variable, elle mesure à quel point ses observations s'écartent de la valeur moyenne
Exemple de deux distributions de même moyenne mais de variance différente¶
Définition et estimateur¶
L'écart-type $\sigma$ correspond à la racine carré de la variance: $$\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2} $$
Pour un échantillon de taille $n$, un bon estimateur (non-biaisé) $s$ de $\sigma$ pourra être calculé par:
coefficient d'assymétrie (skewness) : moment d'ordre 3¶
Il s'agit de la mesure de l'asymétrie par rapport à la moyenne d'une distribution d'une variable aléatoire réelle

By Diva Jain Lien
Il s'agit d'une mesure du degré d'applatissment des queues (par rapport à une loi normale) d'une distribution d'une variable aléatorie réelle
Loi de probabilités rangées par kurtosis:¶
Mesurer l'erreur associées à nos estimateurs¶
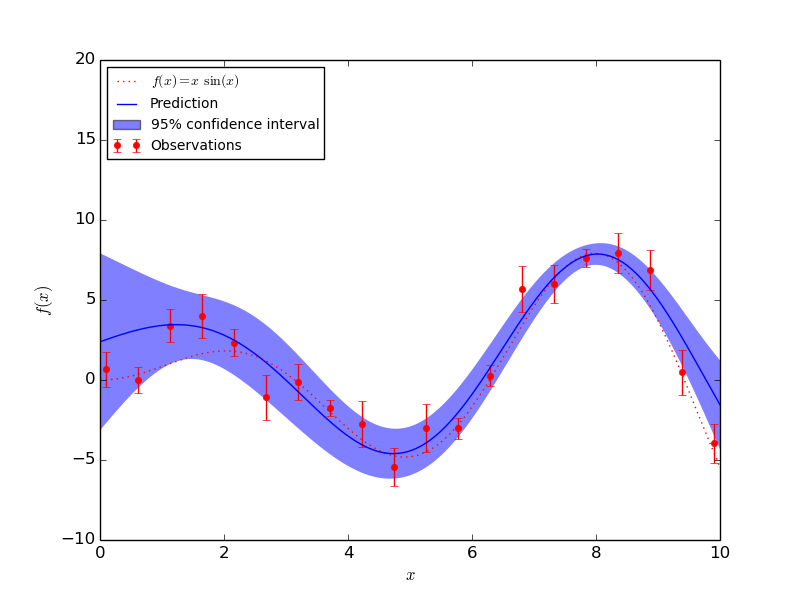
Un intervalle de confiance encadre une valeur réelle que l’on cherche à estimer, souvent pour définir une marge d'erreur entre les résultats d'un échantillonnage et un relevé exhaustif de la population totale
Un intervalle de confiance est associé à un niveau, en général sous la forme d’un pourcentage, qui encadre la probabilité que l'intervalle contienne la valeur à estimer
Exemple d'intervalle de confiance de niveau 50% : Parmi les 20 échantillons tirés suivant une loi normale de moyenne $\mu$ : 50% contiennent la valeur $\mu$ à estimer (en bleu) et 50% ne la contiennent pas (en rouge)
En pratique, on utilise souvent l'intervalle de confiance pour mesurer l'erreur pour commise lorsque l'on utilise des estimateurs d'indicateurs statistiques (comme par exemple la moyenne, la variance, ...)
Les facteurs qui influent sur la largeur de l'IC sont le niveau de confiance, la taille de l'échantillon et la variabilité de l'échantillon.
Un échantillon plus grand produira un intervalle de confiance plus étroit.
De même, une plus grande variabilité dans l'échantillon produit un intervalle de confiance plus large, et un niveau de confiance plus élevé exigerait un intervalle de confiance plus large.
Pour des détails concernant son calcul, vous pouvez lire ce chapitre
Exemple d'intervalle de confiance pour une régression¶
Estimateurs multi-variés¶
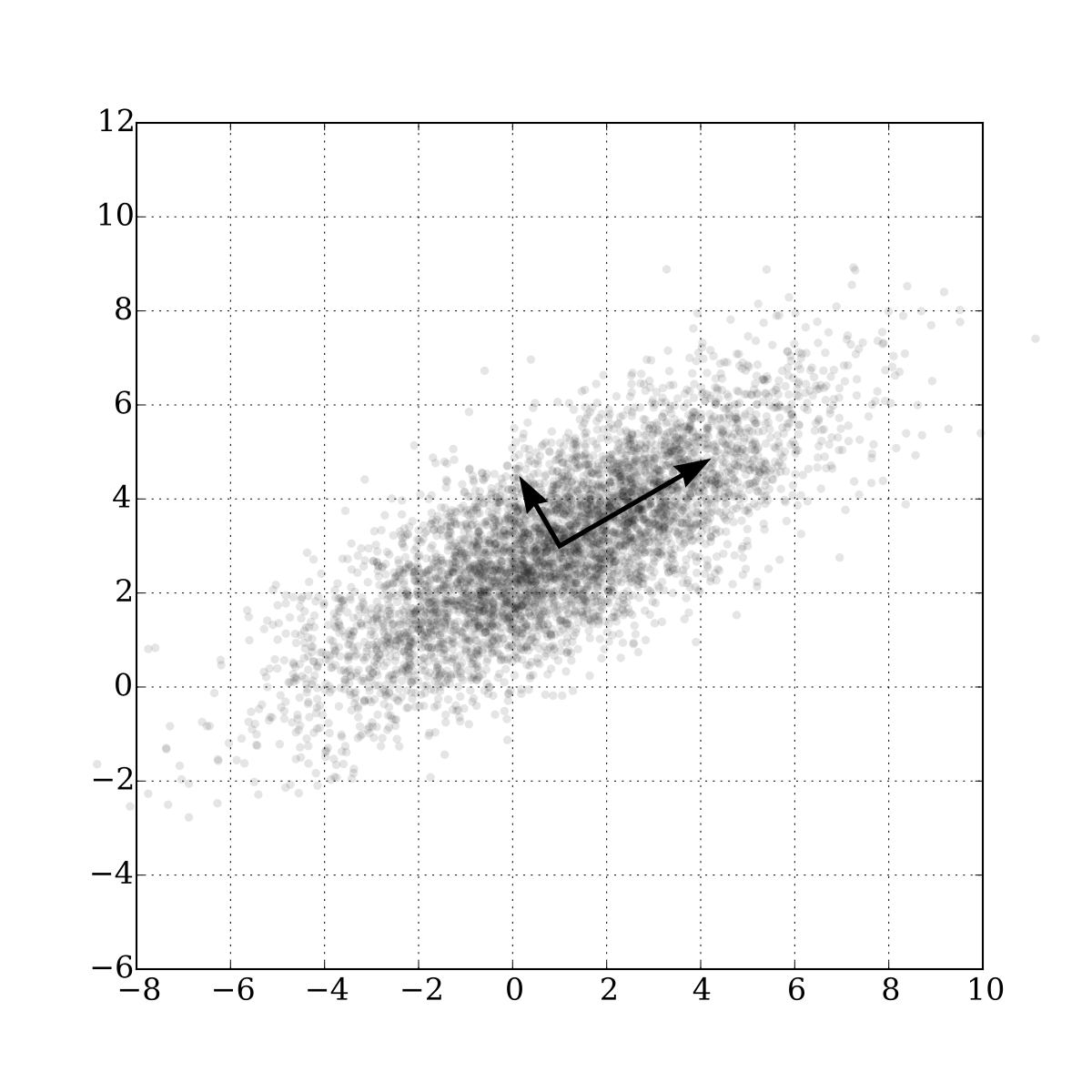
Corrélation¶
Le coefficient de corrélation de Pearson mesure le degré de relation linéaire entre deux variables $X$ et $Y$
Pour la population $N$:
Et pour un échantillon de taille $n$:
Illustrations de différentes corrélations¶
Evolution des corrélations¶
Attention aux mauvaises interprétations:¶
- Deux variables indépendantes ont une corrélation nulle ... mais deux variables ayant une corrélation nulle ne sont pas forcément indépendantes !
- Même si X et Y sont fortement corrélées, cela ne garantit pas que X cause Y !
Exemple de l'Analyse en Composante Principale (ACP)¶
Cette méthode consiste à combiner linéairement les variables de départ de votre dataset ($x_1$, $x_2$, ... $x_p$) pour construire de nouvelles variables, les composantes, qui seront maximalement non corrélées.
En représentant les données dans une nouvelle base constituée par ces composantes, on obtient un espace dont les vecteurs représentent les principales sources de variances du dataset
llustration d'une ACP avec deux composantes¶
Explorons un exemple interactif pour mieux appréndher son mécanisme
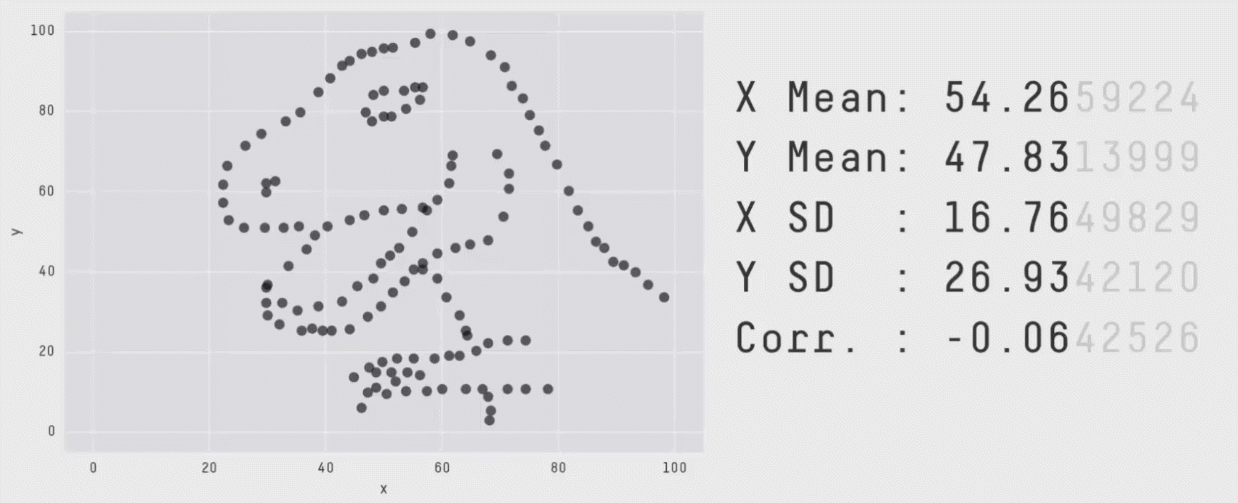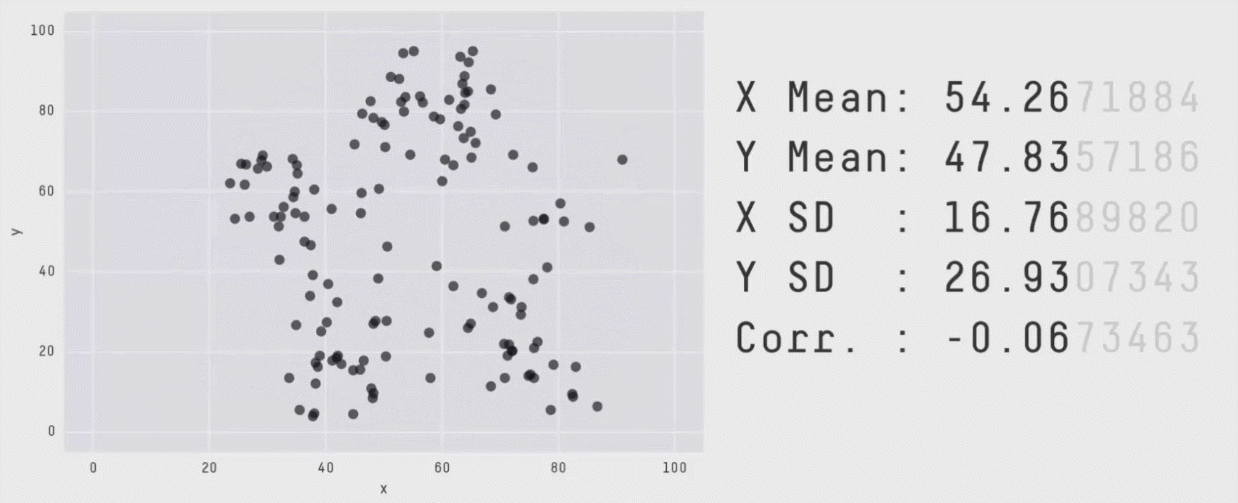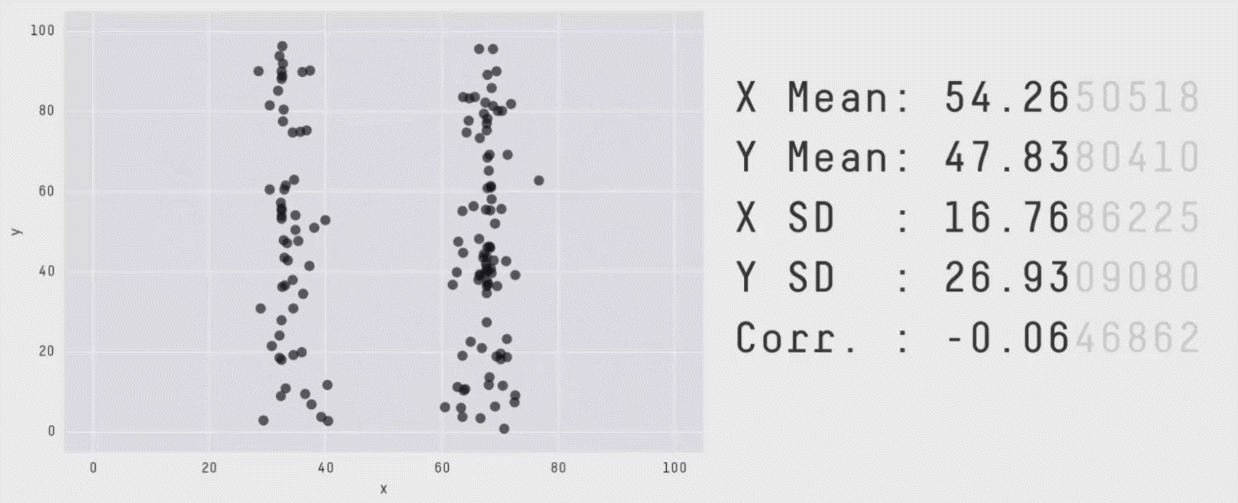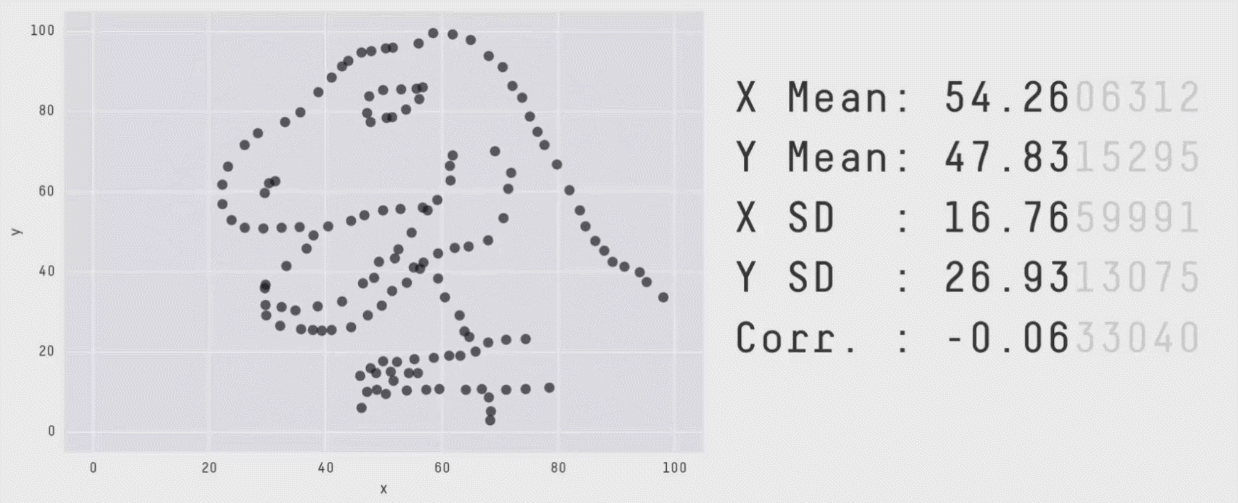
Attention au quartet D'anscombe et au datasaurus¶
Les statistiques descriptives ne sont pas suffisantes pour bien comprendre finement vos données, elle ne vous en donnent qu'un aperçu !!
Vous aurez besoin de faire croiser les indicateurs que vous utiliserez pour bien comprendre vos données
Les estimateurs que nous avons vu sont univariés: il n'opérent que sur une variable à la fois et ne peuvent donc pas capturer de relation entre les variables. Il faut pour cela utiliser des méthodes multivariées
Probabilités¶
Notion d'expérience aléatoire¶
Il s'agit d'une expérience dans laquelle les observations sont aléatoires.
On définit pour chaque expérience l'ensemble des résultats possibles (univers) $\Omega$.
Examples:
- Lancer une pièce $\Omega$ = {Pile, Face}
- Lancer un dé $\Omega$ = {1,2,3,4,5,6}
Lorsque l'on répète plusieurs fois une expérience aléatoire, on obtient une épreuve,par exemple:
$\Omega$ = {(Pile,Pile, Pile),(Face, Pile, Face)}
Union et intersection¶
Pour deux évenements A et B on peut définir:
- $A \cup B$ est réalisé lorsque A ou B est réalisé
- $A \cap B$ est réalisé lorsque A et B sont réalisé simultanément
Probabilité : définition et propriétés¶
Il s'agit d'un réel P(A) tel que $0\leqslant P(A) \leqslant 1$ défini par :
Probabilité conditionelle¶
Si on obtient des informations additionnelles au cours d'une expérience aléatoire, comment mettre à jour une probabilité ?
La probabilité de A sachant B est définie par:
Exemple¶
Considerons l'expérience suivante: piocher deux cartes, une à la fois, sans remplacement dans un jeu de 52 cartes.
Vous piochez un roi (évenement A)
Quelle est la probabilité de piocher un second roi (évenement B) ?
Solution¶
Comme le tirage estt sans remise, les deux événement A et B sont dépendants:
Indépendance statistique¶
A et B son indépedant si et seulement si:
$P(A|B) = P(A)$ (avec $P(B)\neq 0$)
Formule de Bayes¶
On cherche a exprimer $P(B|A)$ en fonction de $P(A|B)$
On sait que:
$P(A \cap B)= P(A)P(B|A)$
$P(B \cap A)= P(B)P(A|B)$
En remarquant que $P(A \cap B) = P(B \cap A)$, on obtient la formule de Bayes:
Cette formule est célèbre car elle a permis definir le principe d'inférence bayesienne et à donné lieu a un courant dans les le domaine des statistiques (on parle de statistiques bayésiennes) et même d'un courant de pensée le bayésianisme!
En data science, on pourrait reformuler la formule de Bayes, pour un évenement consistant à observer les données D sachant la théorie T par:
Avant de réaliser une expérience, on peut se donner un a priori (ou un pari) sur la probabilité P(T) de notre théorie, après une épreuve, on peut estimer la vraissemblance des données obtenues p(D|T) puis on calcule, par la formule, la plausibilité de la théorie P(T|D).
Lorsque l'on répète l'expérience, on peut se servir de la plausibilité calculée comme nouvel a priori et calculer à nouveau la plausibilité de la théorie après cette nouvelle observation.
Ce fonctionnement itératif nous permet de d'affiner itérativement la plausibililté de notre théorie !
Pour une explication détaille, voire cette excellente vidéo de 3Blue1Brown
Il s'agit d'une fonction mathématique qui donne les probabilité d'occurence des différents résultats que peut prendre une (ou plusieurs) variable(s) aléatoire
Graphiquement, on la détermine par l'aire sous la courbe de la densité de probabilité (probability density function) ou de celle de la distribution cumulée (cumulative density function)
Il existe plusieurs loi de probabilité dont on connait la formule, comme la célèbre loi normale
Sa densité de probabilité est définie par la formule:
def plot_normal_distribution(mu, variance):
sigma = math.sqrt(variance)
x = np.linspace(-10, 10, 100)
plt.plot(x, stats.norm.pdf(x, mu, sigma), label=f"μ={mu}, σ²={variance}")
plot_normal_distribution(0, 1)
plot_normal_distribution(1, 2)
plot_normal_distribution(-3, 5)
plt.legend()
plt.show()
On parle souvent de la loi normale centrée ($\mu = 0$) réduite ($\sigma=1$)
Découpage d'une loi normale centré réduite par écart type¶
En pratique, on ne connait que rarement la distribution de probabilité d'une variable lorsque l'on réalise une expérience aléatoire
Par exemple, si on répète le lancer d'une pièce avec une probabilité $p$ de faire pile:
L'évenement "obtenir n fois pile" est décrit par distribution binomiale !
np.random.binomial(n=1, p=0.5, size=10)
array([0, 0, 0, 1, 0, 0, 1, 1, 0, 1])
Au bout de n lancers, on obtient les fréquences:
n = 5
np.random.binomial(n=n, p=0.5, size=10) / n
array([0.8, 0.2, 0.8, 0.4, 0.2, 0.4, 0.4, 0.4, 0.4, 0.8])
n = 5
sns.histplot(np.random.binomial(n=n, p=0.5, size=10000), kde=False);
Quand n est grand, la fréquence du nombre de pile vers une distribution normale !
n = 1000
sns.histplot(np.random.binomial(n=n, p=0.5, size=10000) / n, bins=20, kde=True);
On peut généraliser le résultat précédant à n'importe quelle expérience aléatoire !
Formulation¶
pour n'importe quelle suite de variables aléatoires réélles $X_1, X_2, \cdots X_n$, indépendantes et de moyenne et variance identique :
- leur moyenne $\bar{X}$ converge vers une distribution normale lorsque la taille de l'échantillon n augmente
- elle est centrée autour de la moyenne de la population $\mu$
- avec l'écart type $\frac{\sigma}{\sqrt{n}}$
Ceci est vrai peut inmporte la forme de la distribution de l'échantillon !