Leçon : Preparation de données pour des traitements statistiques¶
Rappel des types d'erreurs courantes¶
- les valeurs manquantes
- les doublons
- les valeurs mal renseignées (par exemple issue d'erreurs de saisie)
- les erreurs du au formatage de données (par exemple les dates)
- les outliers
Généralement les valeurs manquantes et les outliers sont les types d'erreur impactant le plus la performance de votre modèle, et donc celles qu'il faudra traiter avec le plus d'attention.
Différentes étapes de préparation des données¶
- Nettoyage minimal des données
- Gestion des doublons et format de données
- Gestion des donnnées manquantes
- Gestion des données abérantes (outliers)
- Etapes de préparation souvent nécessaires
- Encodage des données catégorielles
- Scaling des données
- Equilibrage des données
- Discrétisation des données
- Etapes visant à améliorer l'information contenue dans le dataset
- Création de features
- Sélection de features
Exemple avec un dataset connu¶
La première chose à faire pour répérer ce type d'erreur est d'explorer un minimum son data set
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
filepath = "https://filedn.eu/lefeldrXcsSFgCcgc48eaLY/datasets/regression/housing-price_train.csv"
raw_df = pd.read_csv(filepath)
raw_df.drop("Id",axis='columns',inplace=True)
raw_df.head()
| MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | LotConfig | ... | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 60 | RL | 65.0 | 8450 | Pave | NaN | Reg | Lvl | AllPub | Inside | ... | 0 | NaN | NaN | NaN | 0 | 2 | 2008 | WD | Normal | 208500 |
| 1 | 20 | RL | 80.0 | 9600 | Pave | NaN | Reg | Lvl | AllPub | FR2 | ... | 0 | NaN | NaN | NaN | 0 | 5 | 2007 | WD | Normal | 181500 |
| 2 | 60 | RL | 68.0 | 11250 | Pave | NaN | IR1 | Lvl | AllPub | Inside | ... | 0 | NaN | NaN | NaN | 0 | 9 | 2008 | WD | Normal | 223500 |
| 3 | 70 | RL | 60.0 | 9550 | Pave | NaN | IR1 | Lvl | AllPub | Corner | ... | 0 | NaN | NaN | NaN | 0 | 2 | 2006 | WD | Abnorml | 140000 |
| 4 | 60 | RL | 84.0 | 14260 | Pave | NaN | IR1 | Lvl | AllPub | FR2 | ... | 0 | NaN | NaN | NaN | 0 | 12 | 2008 | WD | Normal | 250000 |
5 rows × 80 columns
# On va travailler sur une copie du data frame pour comparaison avec le data frame brut
df=raw_df.copy()
Nettoyage minimal des données
Gestion des doublons¶
Cette étape consiste à gérer les doublons présents dans le dataset, c'est à dire différentes informations (encodées dans différentes lignes) qui devraient correspondre à une même information (à fusionner dans une même ligne). Par exemple, la présence de doublons peut se manifester par:
- des données dupliquées : se traite par la méthode dataframe.drop_duplicates()
- des données comportant la même information mais formatée différement : par exemple des dates dans différents formats. Dans ce cas le module datetime de python peut vous aider à gérer ces différences de format
- des différences d'orthographe ou de casse: dans ce cas les méthodes de logique floue peuvent être utiles comme le package fuzzy wuzzy ou fuzzy names
- ... d'autres situations :les expressions régulières pourront souvent vous permmettre de capturer différents schémas récurrent pour les uniformiser
Gestion des valeurs manquantes et les outliers¶
Dans un data set, les données peuvent être manquantes pour plusieurs raisons différentes (données n'ayant pas pu être observées, données perdues, ...). Plusieurs stratégies classiques sont possibles pour gérer vos valeurs manquantes:
Ne rien faire (et travailler avec un gruyère):¶
Lorsque la proportion de données manquantes est faible, on peut envisager de ne pas les traiter, à condition que le modèle que vous utilisez puisse gérer de manière satisfaisante les données manquantes.
En général, c'est une situation que l'on rencontre peu, cette approche n'est pas conseillée !
Supprimer certaines variables:¶
Lorsque la proportion de données manquantes est importante dans certaines variables on peut envisager de les supprimer, en vérifiant que la suppression de ces variables ne réduisent pas trop la performance de votre modèle. Lorsque vous travaillez avec un DataFrame, vous pouvez utilisez la méthode de pandas dataframe.drop()
Je peux choisir de supprimer, les colonnes ayant plus d'un certains % de valeurs manquantes:
percent_missing = df.isnull().sum() * 100 / len(df)
percent_missing.sort_values(ascending=False,inplace=True)
threshold_view = 2
filtered = percent_missing[percent_missing.values > threshold_view]
ax = sns.barplot(x = filtered, y = filtered.index, orient='h');
ax.set_title(f"Répartition du pourcentage de valeurs manquantes"
"supérieures au seuil de {threshold_view}%");
Par exemple, ici je choisi de supprimer les colonnes ayant plus de 70% de valeurs manquantes :
threshold = 70
columns_to_drop = percent_missing[
percent_missing.values > threshold].index
columns_to_drop
Index(['PoolQC', 'MiscFeature', 'Alley', 'Fence'], dtype='object')
df.drop(columns_to_drop, axis='columns', inplace=True)
df.shape
(1460, 76)
Supprimer des observations:¶
Si la variable qui contient des données manquantes est cruciale dans l'analyse, alors mieux vaut créer un sous-échantillon et y supprimer les observations pour lesquels cette variable est manquante.
Par exemple, je peux supprimer les lignes contentant toutes des valeurs manquantes:
df.dropna(how='all',inplace=False).head(5)
| MSSubClass | MSZoning | LotFrontage | LotArea | Street | LotShape | LandContour | Utilities | LotConfig | LandSlope | ... | EnclosedPorch | 3SsnPorch | ScreenPorch | PoolArea | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 60 | RL | 65.0 | 8450 | Pave | Reg | Lvl | AllPub | Inside | Gtl | ... | 0 | 0 | 0 | 0 | 0 | 2 | 2008 | WD | Normal | 208500 |
| 1 | 20 | RL | 80.0 | 9600 | Pave | Reg | Lvl | AllPub | FR2 | Gtl | ... | 0 | 0 | 0 | 0 | 0 | 5 | 2007 | WD | Normal | 181500 |
| 2 | 60 | RL | 68.0 | 11250 | Pave | IR1 | Lvl | AllPub | Inside | Gtl | ... | 0 | 0 | 0 | 0 | 0 | 9 | 2008 | WD | Normal | 223500 |
| 3 | 70 | RL | 60.0 | 9550 | Pave | IR1 | Lvl | AllPub | Corner | Gtl | ... | 272 | 0 | 0 | 0 | 0 | 2 | 2006 | WD | Abnorml | 140000 |
| 4 | 60 | RL | 84.0 | 14260 | Pave | IR1 | Lvl | AllPub | FR2 | Gtl | ... | 0 | 0 | 0 | 0 | 0 | 12 | 2008 | WD | Normal | 250000 |
5 rows × 76 columns
df.shape
(1460, 76)
Imputer les valeurs manquantes (a utiliser avec précaution !) :¶
Une stratégie un peu plus audacieuse (mais qui peut se réveler payante si vous souhaitez conservez plus de données) consiste à remplacer les valeurs manquantes par une valeur estimée. Il existe différentes méthodes d'imputation, variant par la méthode estimation des valeurs manquante à remplacer:
Pour des variables numériques :¶
Imputation unviariée¶
- l'imputation par la moyenne (ou la médiane):
On remplace chaque valeur manquante d'une variable par la moyenne (ou la mediane) des valeurs de cette variable. Pour des variables discrètes, on pourra utiliser la valeur la plus fréquente (le mode) comme estimateur des données à remplacer. Cette méthode d'imputation est implémentée dans scikit-learn par SimpleImputer
Imputation multivariée¶
- l'imputation par la régression:
On remplace chaque valeur manquante $y_i$ par son estimation $\hat y_i$ calculé en faisant une régression à partir d'autres variables disponibles (ne contenant pas ou peu de données manquantes). Cette méthode d'imputation est implémentée dans scikit-learn par IterativeImputer
- l'imputation par la méthode hot-deck aléatoire:
On remplace une valeur manquante $y_i$ par une observation sélectionnée au hasard avec remise (parmi les observations non manquantes)
- l'imputation par la méthode des plus proches voisin:
On remplace une valeur manquante $y_i$ par l'observation correspondant au plus proche voisin parmi les observations non manquantes. Cette méthode d'imputation est aussi implémentée dans scikit-learn par KNNImputer
Imputation univariée des variables catégorielles :¶
On ne peut plus utiliser les méthodes citées plus haut car elle ne sont calculables que sur des variables numériques, il faudra utiliser des méthodes d'imputation spécifiques:
- l'imputation par le mode:
On remplace chaque valeur manquante d'une variable par la valeur la plus fréquente (le mode) comme estimateur des données à remplacer. Cette méthode d'imputation est encore implémentée dans SimpleImputer en utilisant le kwarg strategy = most_frequent
Exemple : Imputation de la variable Electrical par la valeur la plus frequente¶
df.loc[:,"Electrical"].isnull().sum()
1
from sklearn.impute import SimpleImputer
imputation = SimpleImputer(missing_values = np.nan,
strategy = 'most_frequent')
imputation.fit(df["Electrical"].values.reshape(-1,1))
SimpleImputer(strategy='most_frequent')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
SimpleImputer(strategy='most_frequent')
imputation.transform(df["Electrical"].\
values.reshape(-1,1))
array([['SBrkr'],
['SBrkr'],
['SBrkr'],
...,
['SBrkr'],
['FuseA'],
['SBrkr']], dtype=object)
df.loc[:,"Electrical"] = imputation.transform(df["Electrical"].values.reshape(-1,1))
# check that there is no more missing value
df.loc[:,"Electrical"].isnull().sum()
0
Imputation des variables numériques restantes¶
Dans cet exemple on va faire une imputation multivariée (en sélectionnant uniquement les variables numériques) :
numeric_features = df.select_dtypes(include=['float','int'])
numeric_features.shape
(1460, 37)
from sklearn.impute import KNNImputer
imputation = KNNImputer(missing_values=np.nan)
imputed = imputation.fit_transform(numeric_features)
imputed.shape
(1460, 37)
df.loc[:,numeric_features.columns] = imputed
Effet de l'imputation¶
def compare_dist(feature):
fig, axes = plt.subplots(1,2,figsize=(12,3))
sns.histplot(raw_df.loc[:,feature],kde=True, ax=axes[0])
axes[0].set_title(f"Raw {feature}");
sns.histplot(df.loc[:,feature],kde=True, ax=axes[1])
axes[1].set_title(f"Imputed {feature}");
compare_dist("LotFrontage")
Dangers de l'imputation¶
L'imputation doit être utilisé avec précaution car elle introduit à la place des observations manquantes, des données estimées. En conséquence, en fonction de la pertinence et de la justesse de ces estimations, vous risquez d'affecter négativement les performances de votre algorithme de manchine learning.
En particulier, il vous faudra prendre des précautions et vérifier en explorant les données que votre imputation:
- ne modifie pas de manière drastique les relations entre les variables
- ne modifie pas de manière drastique la variance de l'estimation de votre variable d'intérêt (dans le cas de l'apprentissage supervisé il s'agire de votre estimation des labels $y$ ou de la variable à optimiser dans le cas du clustering (par exemple l'inertie dans le cas de K-means))
Les outliers¶
Un outlier peut désigner une valeur aberrante (une valeur probablement erronnée) ou une valeur atypique (qui est inhabituelle mais pas forcément fausse).
En général, il est assez souvent difficile de distinguer ces deux cas de figure pour un outlier, la meilleure solution à votre portée reste d'explorer vos données en calculant des indicateurs statistiques (mediane, ecart-type, corrélations, ...) et en utilisant des visualisations de données .
Identification et traitement des outliers¶
Les identifier supprimer manuellement (par exploration des données)¶
Avec le critère de Tukey¶
Une convention consiste à utiliser le critère de Tukey pour représenter les outliers comme des points se situant en dehors des moustaches d'un diagramme à moustache, ou boxplot
import seaborn as sns
ax = sns.boxplot(data=df.loc[:,["1stFlrSF","2ndFlrSF"]]);
ax.set_ylabel("Surface");
ax.set_title("Boxplots utilisant le critère de Tukey");
Attention, ce critère n'est qu'indicatif, il convient de continuer à explorer les données suspectées, par exemple avec un scatter plot :
ax = df.plot(kind='scatter',
x="1stFlrSF",
y= "2ndFlrSF")
ax.set_title("Surface des étages");
Avec des méthodes automatiques¶
Il est possible d'utiliser des modèles de machine learning spécifiquement entraînés pour détecter des identifier la frontière séparant les inliers des données outliers
Par exemple, scikit-learn propose plusieurs méthodes décrites dans cette page dédiée
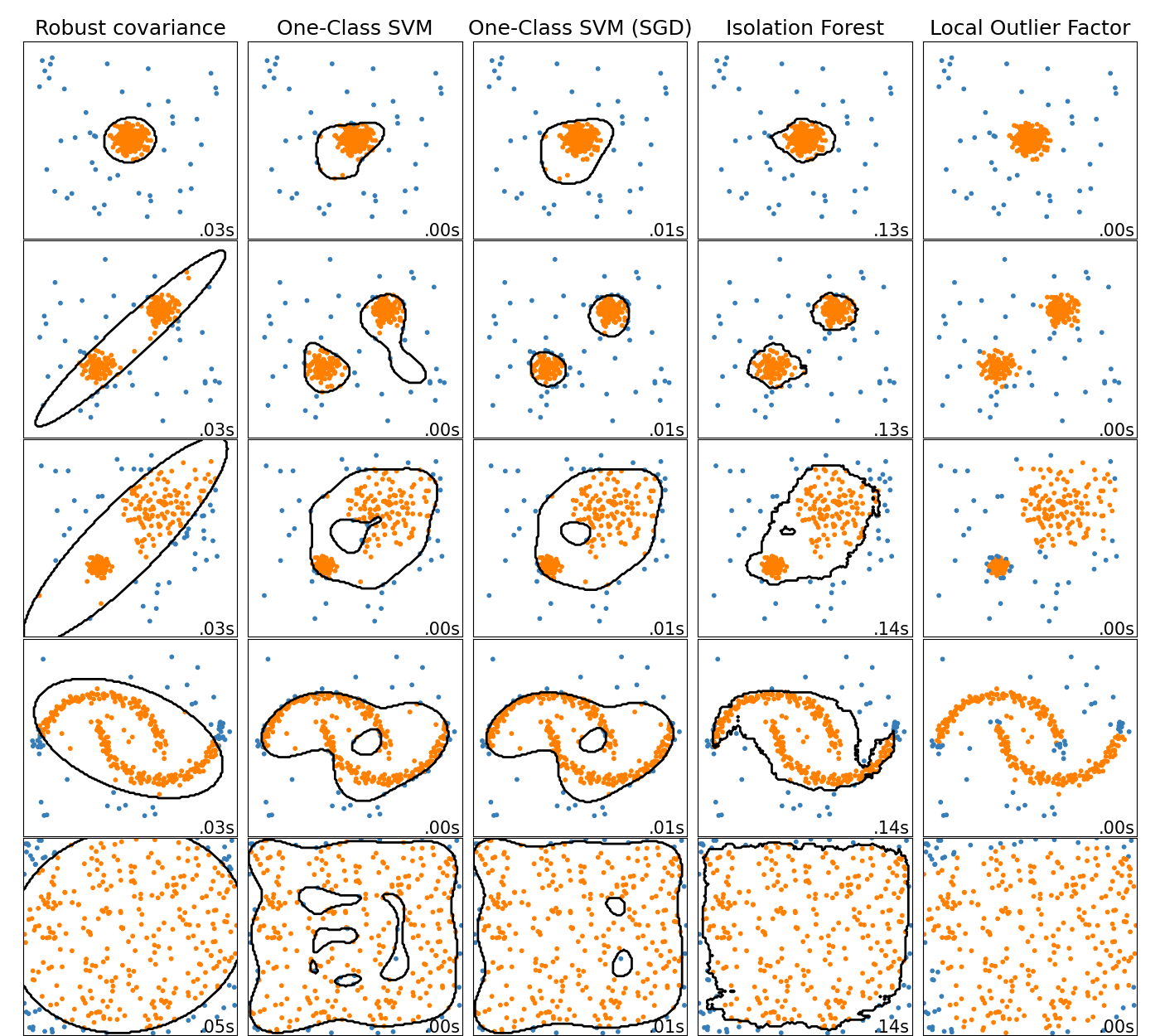
Conserver ces valeurs ?¶
Si vous avez des doutes, conservez les outliers qui pourraient être des valeurs atypiques. Dans ce cas, vous avez plutôt intérêt dans ce cas à utiliser des méthodes d'analyse robustes aux outliers, comme par exemple les modèles qui utilisent des méthodes de régularisation (c'est le cas par exemple des regression ridge et lasso)
Dans tous les cas, je vous conseille d'avoir une démarche itérative et de mesurer à quel point vos traitements affectent la performance générale de vos analyses !
Etapes de traitements supplémentaires
Nous allons voir maintenant d'autres étapes, non indispensables, mais souvent nécessaires dans certaines tâches de data science, en particulier pour le machine learning
Encodage des variables catégorielles¶
Cette étape de traitement consiste à encoder les variables catégorielles en variables numériques afin qu'elle soient utilisables par la plupart des algorithmes de traitement de données. Il existe différentes façons de réaliser cet encodage, par exemple :
Encodage des labels (target)¶
On utilise label encoder qui recode les valeurs de la variable target en valeur numérique de 0 à $n_{classes}-1$
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
le.fit_transform(["paris", "paris", "tokyo", "amsterdam"])
array([1, 1, 2, 0])
Encodage des features¶
Pour encoder des les features catégorielles ordinales, on peut utiliser l'outil ordinal encoder qui va les transformer en série de nombre en préservant la relation d'ordre
oe = preprocessing.OrdinalEncoder()
X = [['Small', 1], ['Tall', 3], ['Tall', 2]]
oe.fit_transform(X)
array([[0., 0.],
[1., 2.],
[1., 1.]])
En revanche, pour les variables catégorielles qui sont non ordinales, afin de ne pas introduire de hiérarchie entre les catégories, on utilise généralement le one-hot-encoder
En pratique, on peut sélectionner toutes les variables catégorielles en utilisantselect_dtypes :
df.select_dtypes('object').info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 1460 entries, 0 to 1459 Data columns (total 39 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 MSZoning 1460 non-null object 1 Street 1460 non-null object 2 LotShape 1460 non-null object 3 LandContour 1460 non-null object 4 Utilities 1460 non-null object 5 LotConfig 1460 non-null object 6 LandSlope 1460 non-null object 7 Neighborhood 1460 non-null object 8 Condition1 1460 non-null object 9 Condition2 1460 non-null object 10 BldgType 1460 non-null object 11 HouseStyle 1460 non-null object 12 RoofStyle 1460 non-null object 13 RoofMatl 1460 non-null object 14 Exterior1st 1460 non-null object 15 Exterior2nd 1460 non-null object 16 MasVnrType 588 non-null object 17 ExterQual 1460 non-null object 18 ExterCond 1460 non-null object 19 Foundation 1460 non-null object 20 BsmtQual 1423 non-null object 21 BsmtCond 1423 non-null object 22 BsmtExposure 1422 non-null object 23 BsmtFinType1 1423 non-null object 24 BsmtFinType2 1422 non-null object 25 Heating 1460 non-null object 26 HeatingQC 1460 non-null object 27 CentralAir 1460 non-null object 28 Electrical 1460 non-null object 29 KitchenQual 1460 non-null object 30 Functional 1460 non-null object 31 FireplaceQu 770 non-null object 32 GarageType 1379 non-null object 33 GarageFinish 1379 non-null object 34 GarageQual 1379 non-null object 35 GarageCond 1379 non-null object 36 PavedDrive 1460 non-null object 37 SaleType 1460 non-null object 38 SaleCondition 1460 non-null object dtypes: object(39) memory usage: 445.0+ KB
Pour l'exemple, encodons les variable LotShape and HouseStyle:
df.loc[:,['LotShape','HouseStyle']].head()
| LotShape | HouseStyle | |
|---|---|---|
| 0 | Reg | 2Story |
| 1 | Reg | 1Story |
| 2 | IR1 | 2Story |
| 3 | IR1 | 2Story |
| 4 | IR1 | 2Story |
On définit et entraine un OneHotEncoder :
from sklearn.preprocessing import OneHotEncoder
enc = OneHotEncoder(handle_unknown='ignore')
enc.fit(df.loc[:,['LotShape','HouseStyle']])
OneHotEncoder(handle_unknown='ignore')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
OneHotEncoder(handle_unknown='ignore')
On peut regarder les catégories unique qui vont être encodées :
enc.categories_
[array(['IR1', 'IR2', 'IR3', 'Reg'], dtype=object),
array(['1.5Fin', '1.5Unf', '1Story', '2.5Fin', '2.5Unf', '2Story',
'SFoyer', 'SLvl'], dtype=object)]
On applique ensuite la transformation :
encoded_features = enc.transform(df.loc[:,['LotShape','HouseStyle']]).toarray()
encoded_features
array([[0., 0., 0., ..., 1., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[1., 0., 0., ..., 1., 0., 0.],
...,
[0., 0., 0., ..., 1., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]])
Scikit-learn permet aussi récupérer le nom des features encodées :
encoded_features_names = enc.get_feature_names_out()
encoded_features_names
array(['LotShape_IR1', 'LotShape_IR2', 'LotShape_IR3', 'LotShape_Reg',
'HouseStyle_1.5Fin', 'HouseStyle_1.5Unf', 'HouseStyle_1Story',
'HouseStyle_2.5Fin', 'HouseStyle_2.5Unf', 'HouseStyle_2Story',
'HouseStyle_SFoyer', 'HouseStyle_SLvl'], dtype=object)
ou l'afficher dans un data frame :
pd.DataFrame(encoded_features,
columns = encoded_features_names).head()
| LotShape_IR1 | LotShape_IR2 | LotShape_IR3 | LotShape_Reg | HouseStyle_1.5Fin | HouseStyle_1.5Unf | HouseStyle_1Story | HouseStyle_2.5Fin | HouseStyle_2.5Unf | HouseStyle_2Story | HouseStyle_SFoyer | HouseStyle_SLvl | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 1 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 3 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 4 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
OHE et la dimensionalité¶
Bien qu'il soit beaucoup utilisé pour sa simplicité, OHE présente l'inconvénient de rajouter beaucoup de colonnes, lorsque les variables à encoder possèdent beaucoup de catégories. C'est pourquoi, il est souvent souhaitable dans ce cas de réduire le nombre de dimensions de votre dataset.
Alternatives a OHE¶
Lorsque vos features à encoder possède beaucoup de catégories, il est préférable d'utiliser des méthodes alternatives à OHE, par exemple :
- la méthode count encoder qui encode les catégories par leur fréquence d'apparition
Cette méthode bien qu'un peu simpliste, peut parfois suffire.
- la méthode hashing encoder qui encode les catégories en générant un hash
Cette méthode, à l'avantage de ne pas être destructive, mais peut être lente et dépend d'hyperparamètre à bien régler.
Pour d'autres méthodes, voir le paquet category encoders
Scaling des données numériques¶
Cette étape de traitement consiste à transformer les variables continues ayant des ordres de grandeur différents en des variables ayant des ordres de grandeur comparables. Bien que généralement non indispensable au fonctionnement direct de votre chaîne de traitement, il est souhaitable de l'utiliser pour:
- Empecher les variables avec des variations de grande amplitude de prendre artificiellement plus d'importance dans votre modèle que celle ayant des variations de faible amplitude (par une mesure de temperatures en °C par rapport a une mesure de tailles de personnes en m)
- Le scaling permet d'interpréter plus facilement l'importance relative des variables pour votre modèle
- Le scaling permet de diminuer les temps de calcul puisqu'il diminue l'ordre de grandeur des variables
La standardisation¶
Elle consiste à simplement changer l'ordre de grandeur de vos variable, sans changer leur distribution. On transforme la variable initiale $X$ en $X'$ suivant:
import numpy as np
import seaborn as sns
from mlxtend.preprocessing import minmax_scaling
import matplotlib.pyplot as plt
# generate 1000 data points randomly drawn from an exponential distribution
original_data = np.random.exponential(size=1000)
# mix-max scale the data between 0 and 1
scaled_data = minmax_scaling(original_data, columns=[0])
# plot both together to compare
fig, ax = plt.subplots(1,2);
sns.histplot(original_data, ax=ax[0]);
ax[0].set_title("Original Data");
sns.histplot(scaled_data, ax=ax[1]);
ax[1].set_title("Scaled data");
La normalisation¶
Elle consiste à modifier la distribution de votre variable d'intérêt pour qu'elle suive une distribution normale. Cette transformation est parfois un prérequis statistique pour certains modèle (comme le Naive Bayes ou généralement les modèles impliquant une gaussienne), dans ce cas il est impératif de l'appliquer. On transforme la variable initiale $X$ en $X'$ qui va varier entre 0 et 1:
from scipy import stats
# normalize the exponential data with boxcox
normalized_data = stats.boxcox(original_data)
# plot both together to compare
fig, ax=plt.subplots(1,2);
sns.histplot(original_data, ax=ax[0]);
ax[0].set_title("Original Data")
sns.histplot(normalized_data[0], ax=ax[1]);
ax[1].set_title("Normalized data");
Le scaling robuste aux outliers¶
Un des problème potentiel avec la standardisation et normalisation est qu'elle est sont sensibles aux outliers (dans leur formule on va utiliser les valeurs extrêmes contenues dans les données ou la variance qui sont sensible aux outliers).
Dans le cas où vos données contiennent encore des outliers, vous pouvez utiliser une méthode de scaling robuste aux outliers (dont le calcul n'est pas trop affecté par leur présence). Par exemple, en utilisant la formule:
où IQR(X) désigne l'Inter Quartile Range (l'écart inter quartile).
Cette méthode est implémentée dans scikit-learn avec la classe RobustScaler
Autres méthodes de scaling¶
Il existe d'autres méthodes de scaling, vous pouvez consultez ce notebook pour visualiser leur effet sur les données
Equilibrage des données (balancing)¶
Cet traitement s'avère nécessaire lorsque le nombre d'observation par classe est fortement déséquilibré: certaines classes peuvent être sous repésentées ou sur représentées, par rapport aux autres classes (par exemple 30% vs 70%)
En apprentissage supervisé, ce problème impacte souvent fortement les performances des algorithmes utilisés: leurs perfomances sera souvent particulièrement mauvaise pour les classes sous représentées (l'algorithme aura plus de mal à généraliser)
Méthodes de ré-échantillonnage aléatoire¶
Pour pallier à ce problèmes on peut utiliser différentes stratégies, les plus simples étant:
- le sous echantillonnage au hasard de la classe majoritaire (random under sampling majority)
- le sur enchantillonnage par duplication, au hasard, de la classe minoritaire (random over sampling minority)
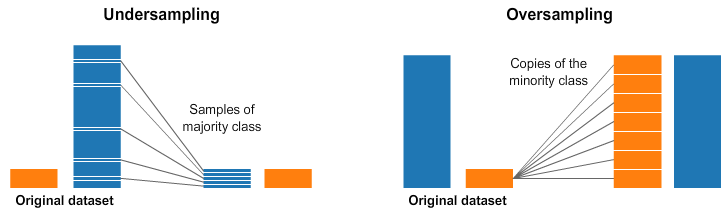
⚠ Attention, les méthodes de sur echantillonnage peuvent causer du data leakage (de l'information provenant d'autre part que le data set d'entrainement est utilisée pour entrainer le modèle) !
Méthodes de ré-échantillonnage avancées¶
Il existe des méthodes de sous échantillonage plus avancées, SMOTE et sa variation, ADASYN opèrent en fabriquant de nouvelles observations de la classe minoritaire en combinant linéairement les observations provenant de la classe sous représentée
SMOTE et ASASYN sont des méthodes de sur échantillonnage, qui génèrent de nouvelles observations à partir d'observations de la classe minoritaire, en se basant sur des combinaisons linéaires du vecteur consititué à partir chacune de ces observations avec ses k plus proches voisins
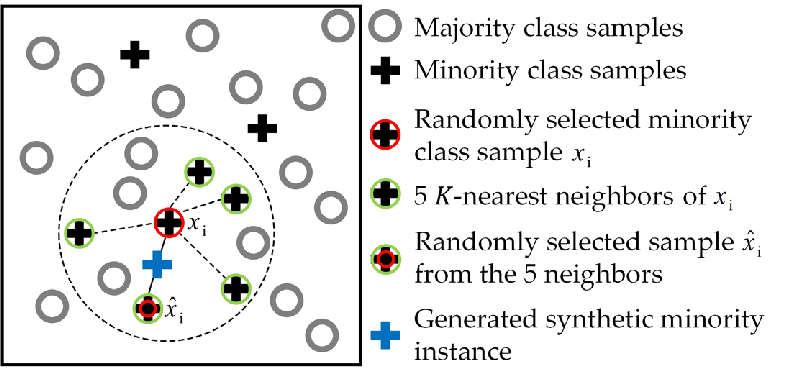
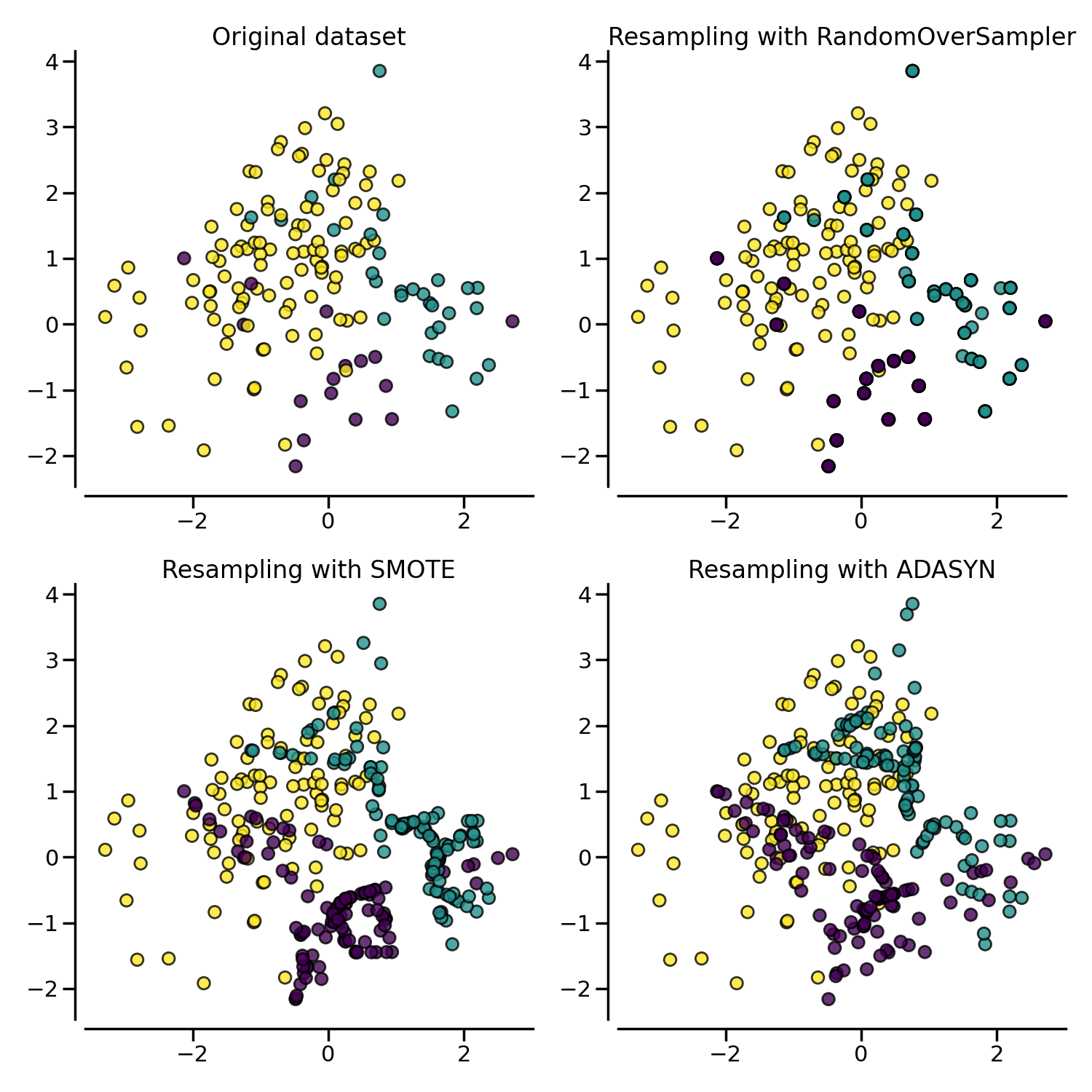
⚠ Attention, on n'utilise les méthodes de ré-échantilonnage que sur le data set d'entrainement, uniquement pour l'apprentissage du modèle. On souhaite garder le data set de test aussi représentatif possible de la réalité !
Pour plus de détails, vous pouvez consultez ce notebook
Discretisation des données¶
On applique ce traitement lorsque l'on souhaite transformer une variable continue en faisant des paquets (bins) pour la rendre discrete. Cela peut servir, par exemple:
- à transformer une tâche de regression en tâche de classification
- faire du feature engineering pour donner plus d'efficacité au modèle
import pandas as pd
import numpy as np
pd.cut(np.array([1, 7, 5, 4, 6, 3]),3, labels=["bad", "medium", "good"])
['bad', 'good', 'medium', 'medium', 'good', 'bad'] Categories (3, object): ['bad' < 'medium' < 'good']
df['SalePriceBinary'] = pd.cut(x = df['SalePrice'],
bins=[df['SalePrice'].min()-1,
df['SalePrice'].mean(),
df['SalePrice'].max()+1],
labels=['cheap', 'expensive'])
df.loc[0:3,['SalePrice','SalePriceBinary']]
| SalePrice | SalePriceBinary | |
|---|---|---|
| 0 | 208500 | expensive |
| 1 | 181500 | expensive |
| 2 | 223500 | expensive |
| 3 | 140000 | cheap |
Améliorer l'information contenue dans le data set
Création de features¶
Cet traitement n'est pas indispensable mais consiste à ajouter de l'information en fabriquant de nouvelles features, pour tenter d'améliorer les performances du modèle
On peut créer des features par différentes méthodes:
- Sur la base d'intutition mathématiques, par exemple en introduisant des features polynomiales:
Exemple : transformer un set de feature ($X_1,X_2$) en ($ X_1, X_2, X_1^2, X_1X_2, X_2^2 $)
- On peut les créer en utilisant des connaissances du domaine, par exemple:
en calculant le BodyMassIndex: $\frac{height}{mass^2}$
- Ou en tentant d'ajouter des informations supplémentaires provenant d'autres sources, comme:
ajouter une variable concernant la présence d'un starbuck près d'une gare dans un problème visant à prédire la fréquentation
Sélection de features¶
Ce traitement consiste à éliminer les features les moins informatives de votre data set afin d'obtenir le modèle le plus parcimonieux, c.a.d celui qui le modèle le plus performant avec le moins de features possibles.
Avantages¶
Réduit le bruit dans les données dues au features peu ou pas informatives
Réduit la complexité du modèle
Evite le problème du fléau de la dimension
Favorise l'interprétabilité du modèle
Réduit le cout computationnel
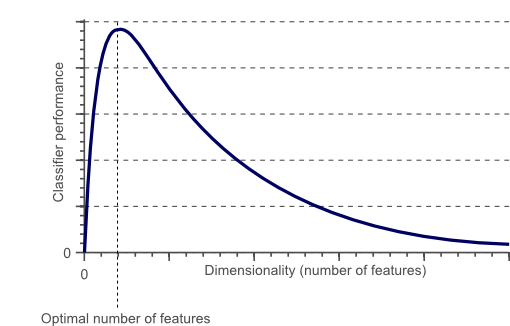
Fléau de la dimension
La performance décroit lorsque on dépasse un nombre critique de features
Le nombre de données nécessaire au augmente exponentiellement avec le nombre de features (dimensions)
Une régle du pouce recommande d'avoir au moins 5 échanntilon d'apprentissage par dimension !
Attention avec l'utilisation du one-hot-encoder --> augmente le nombre de features
Corrélation de Pearson¶
Une des plus simple méthode de sélection consiste à éliminer les features les plus corrélées entre elles, puisqu'elles sont fortement dépendantes et apportent une information redondante
Par seuil: suppression des features moins bien classés¶
Dans cette famille de méthodes on classe les features en calculant un score, puis on supprime les features les moins bien classées
Dans scikit-learn, SelectKbest SelectPercentile, ... sélectionnent les features qui obtiennent les meilleurs scores suivant un critère statistique donné, comme par exemple un test statistique d'indépendance ($\chi^2$)
Example avec le dataset Iris qui contient 4 features:
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
X, y = load_iris(return_X_y=True)
X.shape
(150, 4)
X_new = SelectKBest(chi2, k=2).fit_transform(X, y)
X_new.shape
(150, 2)
On a sélectionné deux features parmi les 4.
Voir en détail l'effet d'une méthode sélection de feature univariée dans cet exemple
Sélection de features multi-variées¶
Il s'agit de méthodes spécifiques à une classe de modèles comme:
- la pénalisation des coefficients de modèles de régression ou classification
- des méthodes spécifiques aux arbres de décision
...
Les méthodes de type wrapper¶
Le principe de ces méthodes consiste à combiner différentes combinaisons de "paquets" de features simultanément (et prenant en compter leur interactions) et garder celles qui favorisent un score élevé du modèle
Par exemple l'elimination récurive de feature procède suivant ces étapes:
- a partir de l'ensemble des features de départ, on calcule leur importance
- on supprime les features les moins importantes
- la procédure est répéte jusqu'a obtenir un nombre désiré de feature
- dans les méthodes ascendantes on part de zero feature, puis on rajoute séquentiellement des features
- dans les méthodes descendantes, on part du set initial de feature, puis on supprime séquentiellement des variables
La réduction de dimensionalité¶
Certaines méthodes de décomposition de matrice comme l'Analyse en Composante Principale ou la Décomposition en Valeur Singulière permettent de trouver une nouvel espace vectoriel pour représenter les variables de votre dataset (plongement), qui exploite mieux certaines propriétés statistiques des données.
Dans ce nouvel, espace, les variables sont exprimées à partir de vecteurs propres, on peut supprimer certaines variables ayant des valeurs propres peu éléves, sans perdre trop d'information.
Par exemple, on peut ranger les composantes ainsi calculées par pourcentage de variance expliquée :
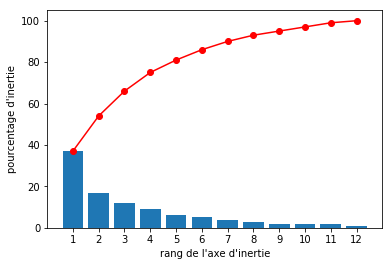
On peut ensuite faire le plongement inverse pour exprimer les variables à partir de l'espace vectoriel de départ, et on obtient alors un data set reconstruit avec moins de variables
Attention au data leakage !¶
Le data leakage (fuite de données) est un phénomène qui survient lorsque l'on utilise, au moment de l'apprentissage de l'information qui ne devrait pas être accessible au modèle.
!!! C'est un phénomène a éviter absolument car il risque de compromettre la capacité de votre modèle à généraliser !!!
Par exemple, si vous faites un scaling de variable en utilisant la totalité du data set, lorsque vous allez faire une validation croisée, vous utiliserez dans les folds pour la validation, des variables ayant été scalées à partir de tout le data set
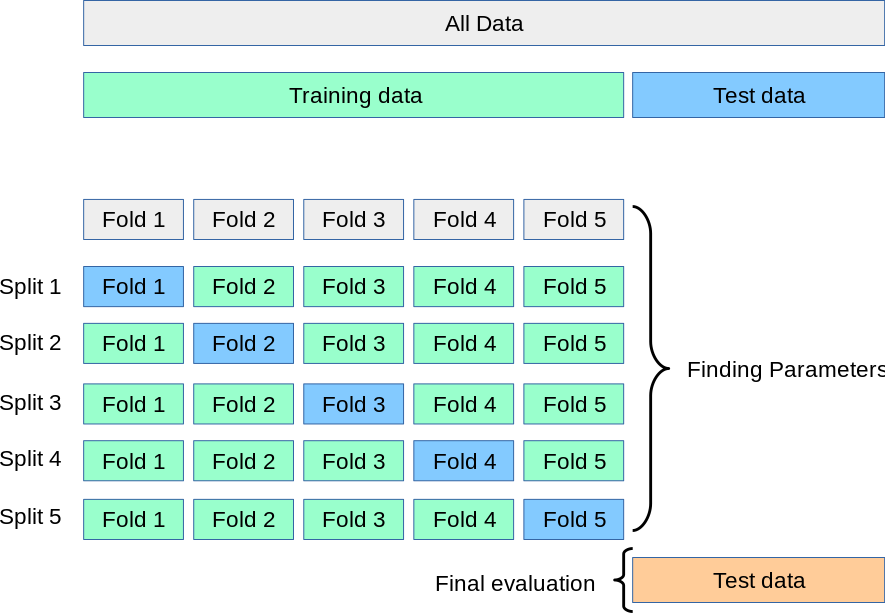
Solution : Utiliser l'objet pipeline de sckit-learn pour exécuter le scaling pendant la cross validation
Voir cet article pour apprendre en détail les différents cas de data leakage