Leçon : Méthodes ensemblistes

Principe général

Il consiste à combiner différents modèles que l'on va entrainer chacun sur toute ou partie des données, puis de combiner leur résultats par des méthodes de consensus pour donner une prédiction finale.

La combinaison des résultats des modèles entraînés ensemble permet généralement de réduire l'erreur et d'obtenir de meilleures performances que les modèles pris seuls séparément!

Le résultat final est obtenu par une méthode de consensus des prédictions des apprenants individuels, en général:

• tâche de régression: la moyenne des prédictions (régression)
• tâche de classificiation: un vote à la majorité des classes prédites (soft voting) ou calculer la moyenne des classes prédites et garder la classe avec la probabilité la plus élevée (hard voting)

En général, on entraine un ensemble d'apprenants faibles, c.a.d des modèles dont les performances individuelles sont faibles (un peu meilleure que les réponses au hasard), principalement pour des raisons de ressources computationnelles insuffisantes, mais il est possible de faire des ensembles avec n'importe quel types de modèle.

Pour cette raison, on utilise souvent les arbres de décision comme apprenants faibles.

Familles de méthodes ensemblistes

Nous allons voir 3 principales méthodes ensemblistes:

• le bagging
• le boosting
• le stacking

Retour sur les arbres de décision

Il s'agit d'un algorithme de machine learning supervisé hierarchique:

• utilisables pour les tâche de classification et régression
• pouvant modéliser des tendances non linéaires
• ils "découpent" les données suivant des régles simples, ce qui les rend facile à interpréter

Arbres de décision pour la classification

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris

# on utilise encore le dataset iris pour la démo
iris = load_iris()
data = pd.DataFrame(data= np.c_[iris['data'], iris['target']],
                     columns= iris['feature_names'] + ['target'])
data.drop(columns=['sepal length (cm)', 'sepal width (cm)'], inplace=True)
data.head(3)

	petal length (cm)	petal width (cm)	target
0	1.4	0.2	0.0
1	1.4	0.2	0.0
2	1.3	0.2	0.0

X = data.drop(columns=['target']).values
y = data.target.values

# On entraine un DecisionTreeClassifier
from sklearn.tree import DecisionTreeClassifier
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=2)
tree_clf.fit(X,y)

DecisionTreeClassifier(max_depth=2, random_state=2)

from sklearn import tree
tree.plot_tree(tree_clf,
               feature_names = data.drop(columns=['target']).columns,
               class_names=['0','1','2','3'], 
               rounded=True, filled=True);

Critère de division des noeuds

Ce critère mesure la qualité d'une division, par défaut c'est le critère de Gini qui mesure l'impureté d'un noeud (entre 0 et 1) :

$$Gini(node) = 1 - \sum{p_i^2}$$

$p{_i}$ étant le ratio d'observation d'appartenance à la classe i pour chaque noeud

# Calcul du critère de Gini du noeud vert
1 - 0**2 - (49/54)**2 - (5/54)**2

0.1680384087791495

Construction d'un arbre

1. L'algorithme démarre du noeud racine contenant toutes les données du dataset.

Puis il répète les étapes suivantes pour chaque séparation:

2. Puis il teste différentes combinaison de (features, seuils) pour séparer les données en 2 nouds fils.

3. Pour chaque combinaison, il calcule une moyenne pondérée (par le nombre de noeuds fils) du critère de classification.

4. L'algorithme sélectionne la combinaison avec la valeur le plus faible.

5. L'algorithme sépare le data set en noeud fils.

6. La croissance de l'arbre s'arrète lorsque le critère de division ne s'améliore plus ou qu'un critère de limitation de croissance est atteint max_depth,min_samples_split, min_samples_leaf.

7. La prédiction finale est donnée par une mesure de consensus du noeud selectionné: la classe la plus fréquente pour la classification.

Prédiction

• Lorsque l'on rencontre une nouvelle donnée on traverse l'arbre jusqu'a la feuille
• La prédiction finale correspond à la classe la plus représentée dans chaque feuille

# prediction de la cellule verte
print(tree_clf.predict([[4,1]]))

[1.]

print(tree_clf.predict_proba([[4,1]]))
# il le s'agit pas réellement de probabilité, mais plutôt d'un ratio

[[0.         0.90740741 0.09259259]]

On peut voir les arbres de décision comme des classifieurs "orthogonaux"

import matplotlib.pyplot as plt
def plot_decision_regions(X, y , classifier, features=[0,1], n_classes = len(np.unique(y)), 
                          figsize = (5,5), cmap=plt.cm.RdYlGn, plot_colors='ryb',
                          plot_step = 0.02):
    
    # keep only a pair of features
    X = X[:,features] 
    
    # Plot the decision boundary
    fig, ax = plt.subplots(1, 1, figsize=figsize)

    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(
        np.arange(x_min, x_max, plot_step), np.arange(y_min, y_max, plot_step)
    )
    plt.tight_layout(h_pad=0.5, w_pad=0.5, pad=2.5)

    Z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    cs = plt.contourf(xx, yy, Z, cmap=cmap)

    plt.xlabel(iris.feature_names[features[0]])
    plt.ylabel(iris.feature_names[features[1]])

    # Plot the training points
    for i, color in zip(range(n_classes), plot_colors):
        idx = np.where(y == i)
        plt.scatter(
            X[idx, 0],
            X[idx, 1],
            c=color,
            label=iris.target_names[i],
            cmap=plt.cm.RdYlBu,
            edgecolor="black",
            s=15,
        )
    plt.title("Decision surface")
    plt.legend(borderpad=0, handletextpad=0)        

plot_decision_regions(X, y, tree_clf)

Comparaison des frontières de decision avec différents classifieurs

Arbres de décision pour la régression

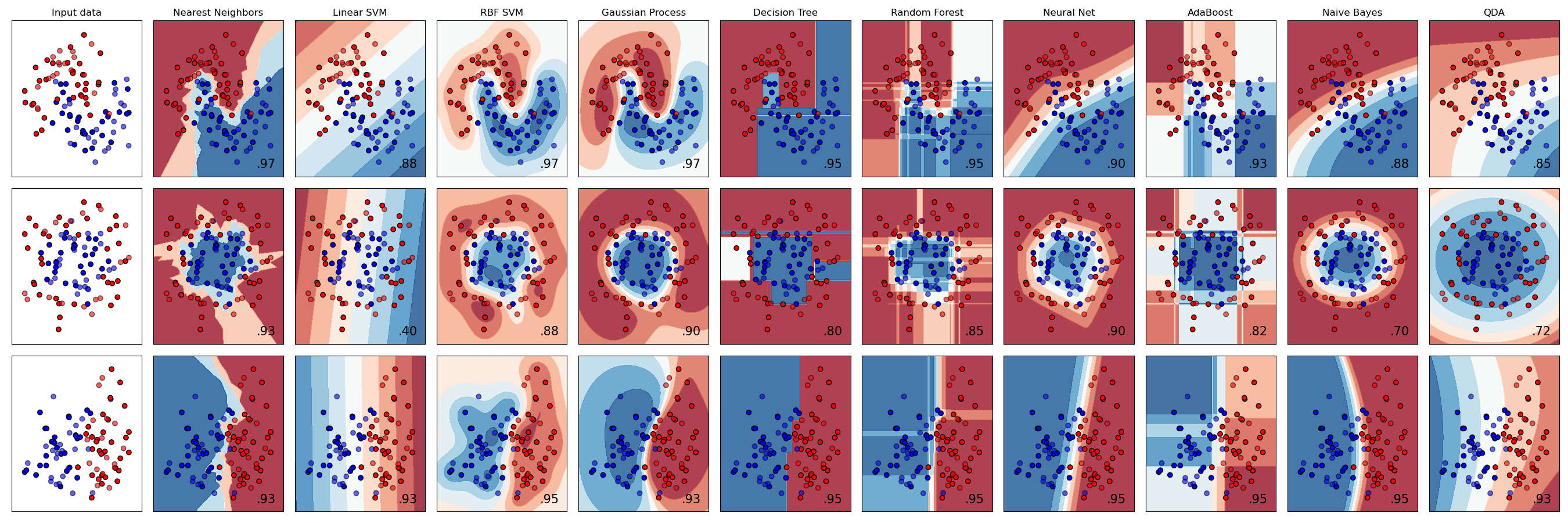
Critère de division des noeuds

Pour la régression on utilise souvent comme critère la moyenne de la somme des erreur que l'on essaye de minimiser, pour chaque noeud contenant $n$ observations:

$$SSE(node) = \sum_{i=1}^n (y-\hat y)^2$$

Construction de l'arbre de régression

On suit les même étapes que pour l'abre de classification, seule la manière de faire la prédiction finale change:
7. La prédiction finale est donnée par une mesure de consensus du noeud selectionné, souvent la moyenne de la feuille apres parcours de l'arbre

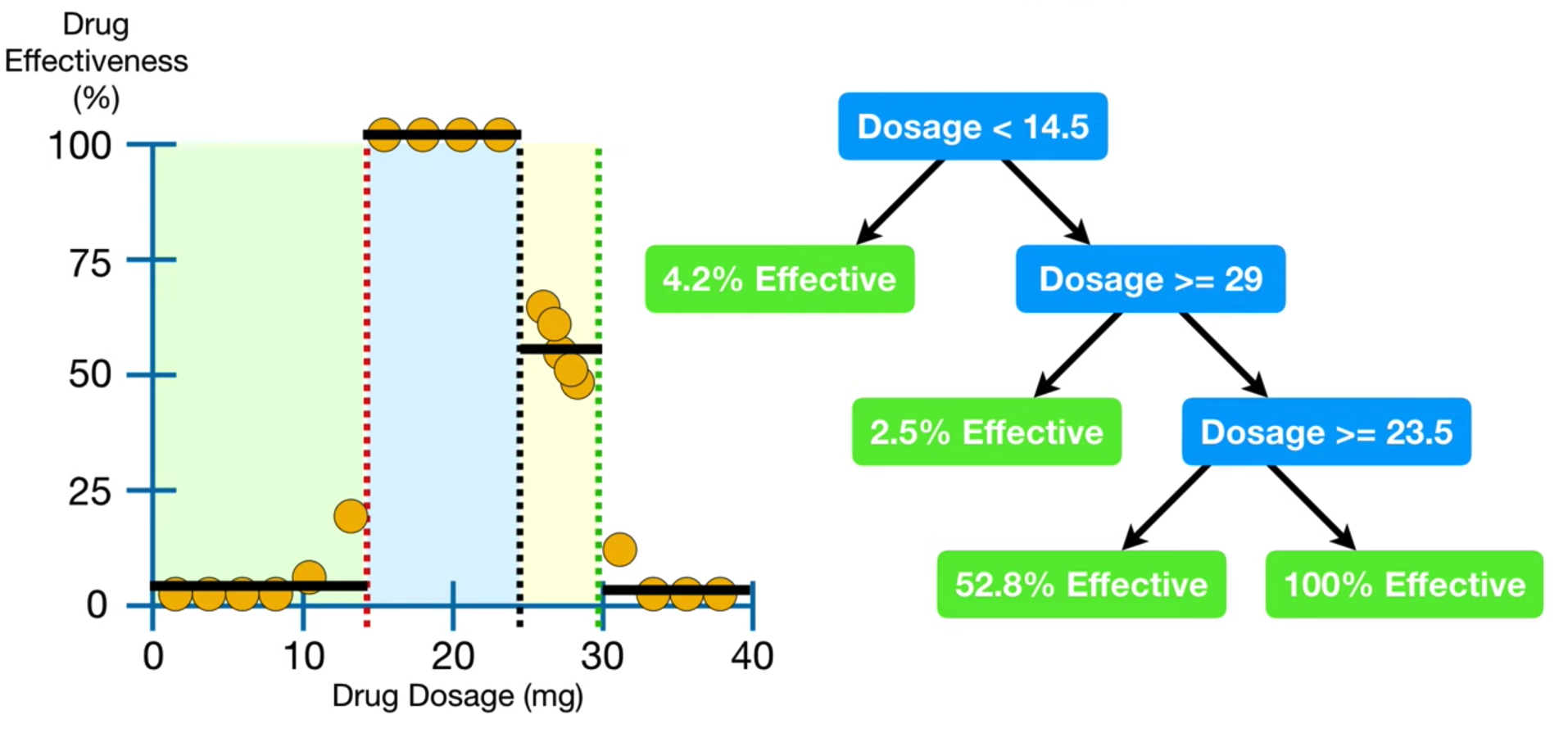
Le bagging (Boostrap Aggrégating)

Cette méthode consiste a aggréger un grand nombre d'apprenants faibles qu'on entraine en parallèle sur des échantillons crées par une méthode d'échantillonage aléatoire du dataset.

L'intêret principal de cette méthode consiste à introduire de la randomisation dans la construction des apprenants faible ce qui permet de réduire la variance globale du modèle aggrégé

L'algorithme RandomForest est un exemple de bagging d'abre de décision ! Dans ce cas, les apprenants faibles sont des arbres de décision dont la croissance individuelle est randomisée

Les méthodes d'échantillons aléatoires du dataset

Il existe différentes manières de "fabriquer" les échantillons aléatoires sur lesquels seront entraînés les apprenants faibles à partir du data set d'origine, ce qui constitue autant de variantes du bagging:

• le Bagging: les échantillons aléatoires sont tiré au hasard, avec remise
• le Pasting: les échantillons aléatoires sont tiré au hasard, sans remise
• les Random Subspaces: les échantillons aléatoires sont tirés au hasard sur un sous ensemble des features
• les Random Patches: les échantillons aléatoires sont tiré au hasard, à partir d'un sous ensemble d'observations et de features

Dans la pratique, lorsque l'on utilise la méthode du Bagging, on utilise très souvent la méthode du bootstrap pour fabriquer les échantillons aléatoires avec remise

Exemple pour le RandomForest:

Aggrégation des apprenants faible et décision finale

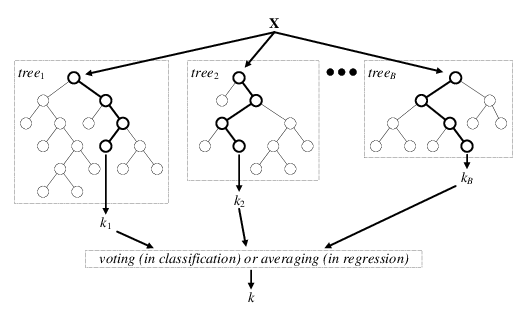
Le résultat final est obtenu par une méthode de consensus des prédictions des apprenants individuel

Exemple avec le data set moon

from sklearn.datasets import make_moons
n=600
X_moon,y_moon = make_moons(n_samples=n, noise=0.25, random_state=0)
plt.scatter(X_moon[:,0], X_moon[:,1], c=y_moon);

Avec un RandomForestClassifier

from sklearn.ensemble import RandomForestClassifier

rf = RandomForestClassifier(max_depth=5,oob_score=True)
rf.fit(X_moon, y_moon)
plot_decision_regions(X_moon, y_moon, classifier=rf)

Ou un bagging de KNNs

from sklearn.ensemble import BaggingClassifier
from sklearn.neighbors import KNeighborsClassifier

weak_learner = KNeighborsClassifier(n_neighbors=3)
bagged_model = BaggingClassifier(weak_learner, n_estimators=40,oob_score=True)

bagged_model.fit(X_moon, y_moon)
plot_decision_regions(X_moon, y_moon, classifier=bagged_model)

Out-of-bag samples

en choisissant l'option oob_score_ on peut estimer l'erreur de généralisation en calculant un score à partir d'un pseudo test set de donnée, mis de coté

print(f"Score on test set: {rf.score(X_moon,y_moon)}")
print(f"Score with out-of-bag: {rf.oob_score_}")

Score on test set: 0.9466666666666667
Score with out-of-bag: 0.9166666666666666

Feature importance

from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_validate

data, target = load_iris(as_frame=True, return_X_y=True)

X_train, X_test, y_train, y_test = train_test_split(
        data, target, test_size=0.3, random_state=42)

rf = RandomForestClassifier(max_depth=5,oob_score=True)
rf.fit(X_train, y_train)
cv_results = cross_validate(rf, X_train, y_train, cv=5)

print(f"Cross-validated training & score on validation set: {cv_results['test_score'].mean()}")
print(f"Score on test set: {rf.score(X_test,y_test)}")

Cross-validated training & score on validation set: 0.9428571428571428
Score on test set: 1.0

import seaborn as sns
feature_scores = pd.Series(rf.feature_importances_,index=data.columns).sort_values(ascending=False)
sns.barplot(x=feature_scores, y=feature_scores.index)
plt.xlabel('Feature Importance Score')
plt.ylabel('Features')
plt.title("Feature importance")
plt.show()

Avantages et inconvénients

Avantages

• Réduit la variance (et donc l'overfitting) du modèle des apprenants faibles aggrégés
• Peut être appliqué à n'importe quel type d'apprenant faible

Inconvénients

• Temps d'entrainement généralement important important
• La structure du modèle rend son interprétation moins facile

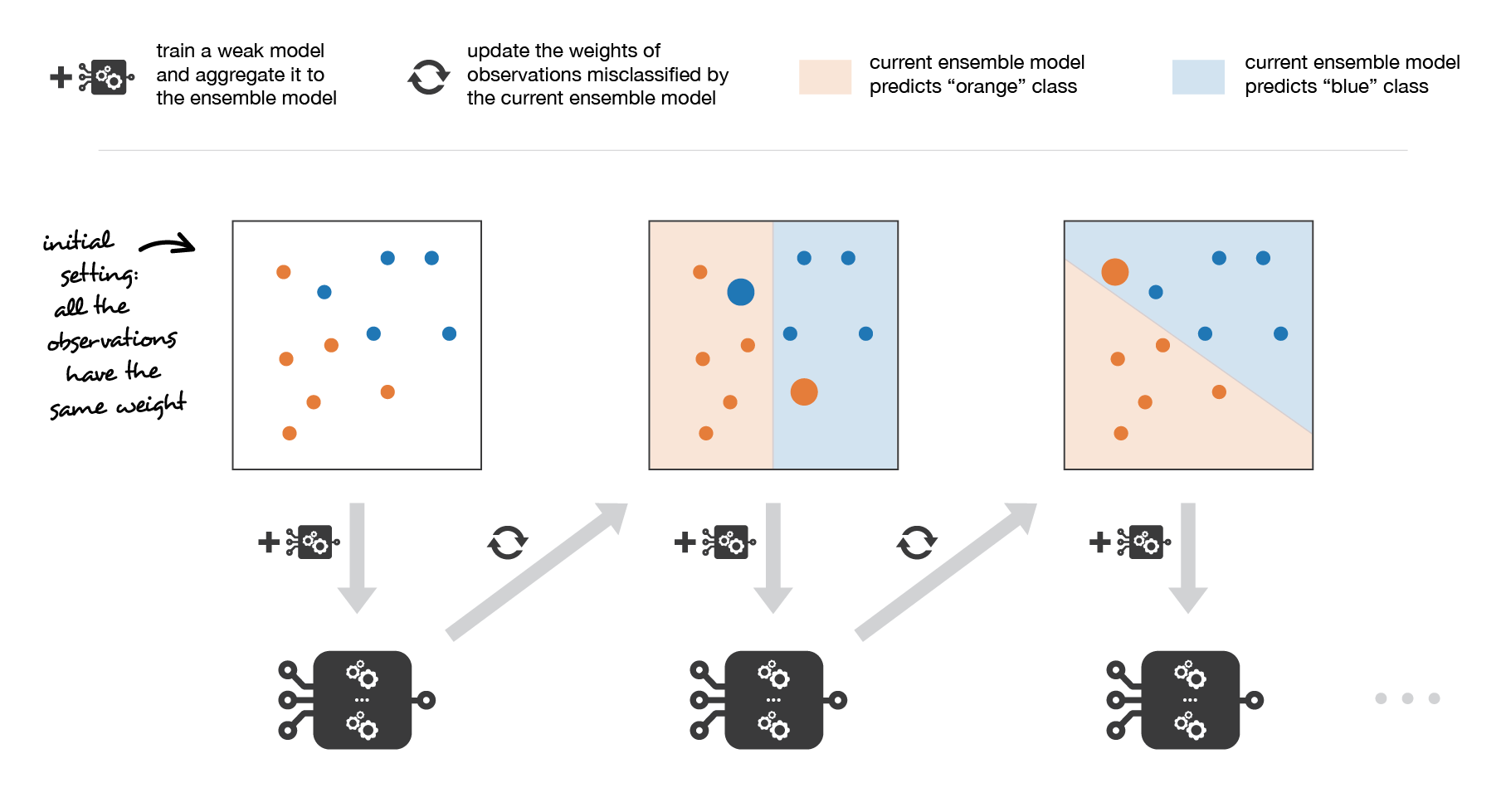
Le Boosting

Le boosting consiste à entrainer ensemble une séquence d'apprenants faibles qui apprennent des erreurs de leur prédécesseurs

Principe :

• Il s'agit d'un modèle d'ensemble séquentiel
• La méthode vise à réduire le biais du modèle d'ensemble ainsi formé
• Au fur et a mesure des itérations, elle permet de privilégier les observations qui sont difficiles à prédire en donnant plus de poids aux échantillons et aux modèles individuels qui apprennent sur ces échantillons
• Le résultat final est obtenu par une méthode de consensus des prédictions des apprenants individuel

Adaboost (Adaptative boosting)

C'est un algorithme de boosting populaire car simple et relativement performant

Principe et étapes:
On définit le modèle d'ensemble final $a_M$ comme la somme pondérée de $M$ apprenants faibles : $a_M = \sum_{m=1}^{M} c_m.a_m$

0. Assigner un poids initial $c=\frac{1}{n}$ aux n observations
1. Entrainer le meilleur $m$ apprenant faible parmi les $M$ sur les observations pondérées
2. Pour chaque itération:

• si l'erreur de prédiction est faible, $c_m$ est diminué
• si l'erreur de prédiction est importante, $c_m$ est augmenté

3. Mettre a jour le modèle d'ensemble $a_m = a_{m-1} + c_m.a_m$ et pondérer les observations avec les poids $c_m$ mis à jour

4. Entrainer un nouvel apprenant faible sur sur les observations pondérées

5. Répéter les étapes 3 et 4 jusqu'a ce que l'erreur de prédiction atteint un seuil

d'apres Josep Rocca

Décision finale

Dans scikit learn, il est implémenté pour la classification, AdaBoostClassifier ou la régression,AdaBoostRegressor

Exemple avec un AdaBoost composé d'arbre de décision

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier


adaboost = AdaBoostClassifier(
    DecisionTreeClassifier(max_depth=3),
    n_estimators=50)
adaboost.fit(X_train,y_train)
cv_results = cross_validate(adaboost, X_train, y_train, cv=5)

print(f"Cross-validated training & score on validation set: {cv_results['test_score'].mean()}")
print(f"Score on test set: {adaboost.score(X_test,y_test)}")

Cross-validated training & score on validation set: 0.9428571428571428
Score on test set: 1.0

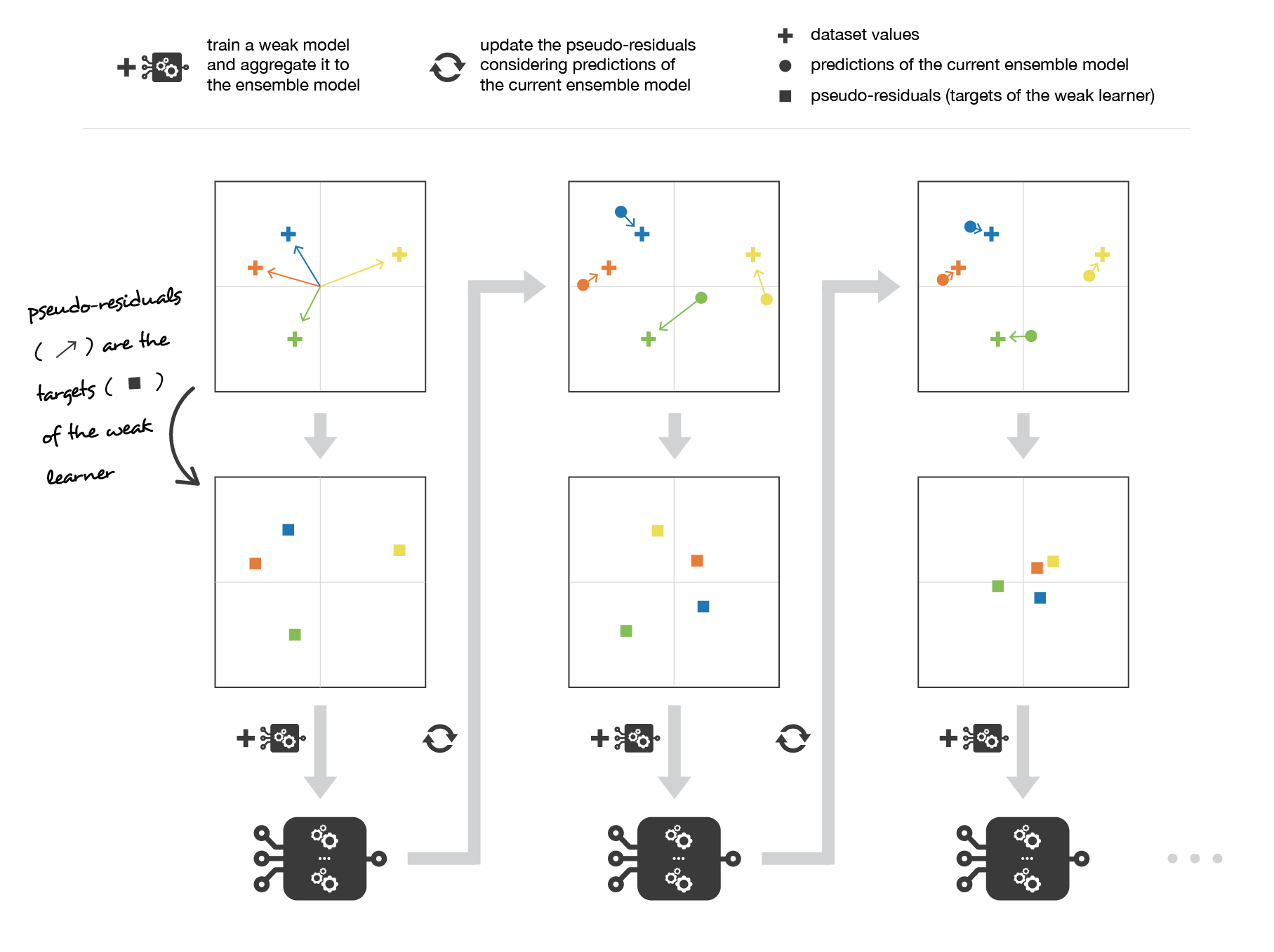
Gradient Boosting

Il peut se voir comme une généralisation d'adaboost, dans lequel on utilise l'algorithme de la descente de gradient comme méthode d'optimisation.

Principe et étapes:

Il reprend les mêmes étapes qu'Adaboost avec la particularité d'utiliser la descente du gradient pour mettre a jour les poids $c_m$:
Etape 3: Mettre a jour le modèle d'ensemble $a_m = a_{m-1} - c_m \times \nabla_{a_{m-1}}Loss(a_{m-1})$ et pondérer les observations avec les poids $c_m$ mis à jour

d'apres Josep Rocca

Implémentations

Dans la plupart des implémentations, le gradient boosting est utilisé avec des arbres de décisions uniquement:

• dans scikit-learn, GradientBoostingClassifier et GradientBoostingRegressor

from sklearn.ensemble import GradientBoostingRegressor
gb = GradientBoostingRegressor(
    n_estimators=100, 
    learning_rate=0.1,
    max_depth=3
)
gb.fit(X_train,y_train)
cv_results = cross_validate(adaboost, X_train, y_train, cv=5)

print(f"Cross-validated training & score on validation set: {cv_results['test_score'].mean()}")
print(f"Score on test set: {gb.score(X_test,y_test)}")

Cross-validated training & score on validation set: 0.9428571428571428
Score on test set: 0.9881685629476077

XGBoost (eXtreme Gradient Boosting)

XGboost est une librairie optimisée et disbtribuable qui implémente le gradient boosting pour les arbres de décision. Elle est très populaire et souvent utilisée en production en data science ou dans les concours

import xgboost as xgb
from sklearn import metrics
from sklearn.model_selection import GridSearchCV 

def auc(m, train, test): 
    return (metrics.roc_auc_score(y_train,m.predict_proba(train)[:,1]),
                            metrics.roc_auc_score(y_test,m.predict_proba(test)[:,1]))

# Instance & définition de la grille de parametres
model = xgb.XGBClassifier()
param_dist = {"max_depth": [10,30,50],
              "min_child_weight" : [1,3,6],
              "n_estimators": [200],
              "learning_rate": [0.05, 0.1,0.16],}
# grid search
grid_search = GridSearchCV(model, param_grid=param_dist, cv = 3, 
                                   verbose=10, n_jobs=-1)
grid_search.fit(X_train, y_train)

grid_search.best_estimator_

model = xgb.XGBClassifier(max_depth=50, min_child_weight=1,  n_estimators=200,\
                          n_jobs=-1 , verbose=1,learning_rate=0.16)
model.fit(X_train,y_train)

auc(model, X_train, test)

LightGBM

LightGBM est une également très populaire, qui implémente le gradient boosting pour les arbres de décision ayant les propriétés suivantes:

• Entrainements rapides et performants
• Faible usage de la mémoire
• Supporte le calcul parallèle, distribué et sur GPU
• Capable de gérer des grandes quantités de données

CatBoost

Il s'agit d'un framework qui implémente le gradient boosting sur les arbres de décision, avec un grand nombre de fonctionnalités, dont l'entraînement sur GPU

Avantages & Inconvénients

Avantages

• Réduit le biais du meta-modèle des apprenants faibles aggrégés
• En général leur performances sont meilleures que celles des modèles de bagging

Inconvénients

• Temps de calculs importants
• Méthode sensible aux outliers (puisque il donne plus de poids aux apprenenants individuels qui ont de mauvaises performances)

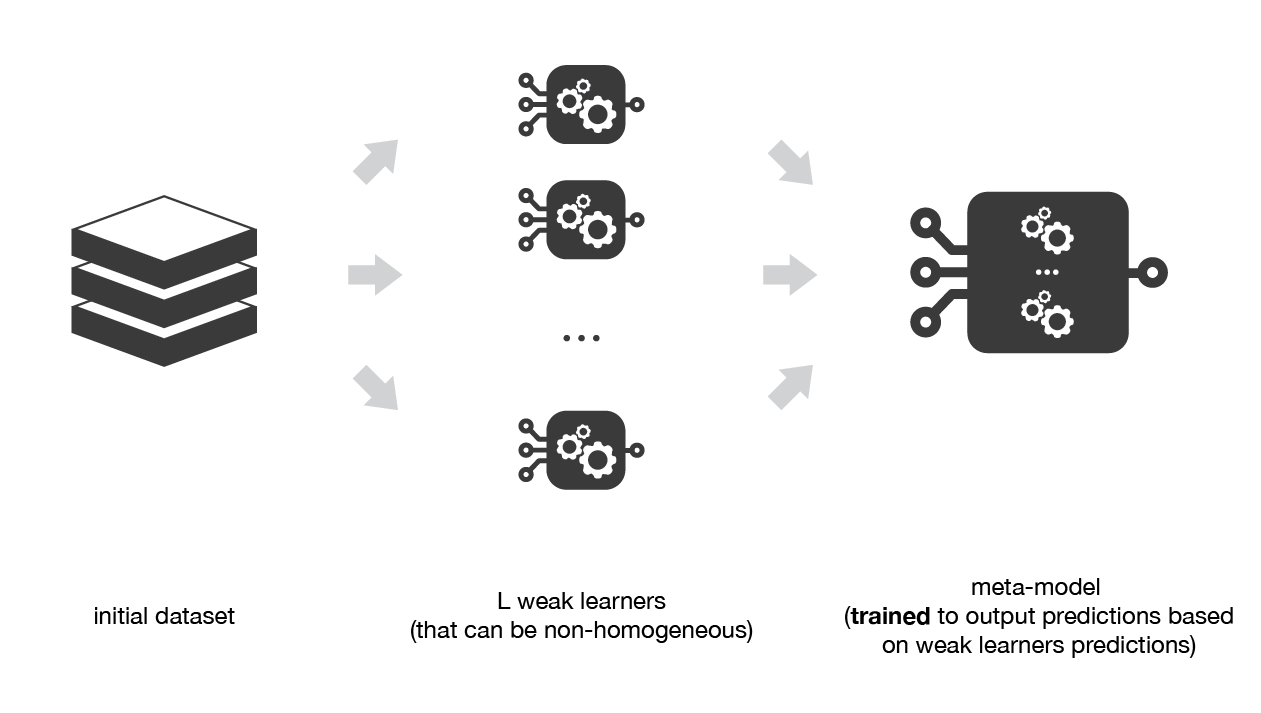
Le Stacking

Le principe du stacking consiste à combiner des modèles individuels et passer leur prédictions en entrée à un modèle de sortie qui produit la décision finale

Principe:

• Différents modèles hétérogènes sont entrainés pour capturer différentes propriétes des données
• Les résultats sont aggrégés comme entrée d'un modèle de sortie (généralement simple)

Etapes:

• Séparer les données en plusieurs folds de validation croisée
• Pour chaque split, entrainer, sur chacun de des folds d'entraînement les modèles individuels)
• Pour chaque split, entainer le modèle de modèle de sortie sur le fold de "validation" restant
• Le modèle de sortie donne la prédiction finale

d'apres Josep Rocca

Implémentations

Dans scikit-learn, différents modèles sont implémentés à la fois pour la classification et la régression:

• VotingClassifier & VotingRegressor: combinent des apprenants individuels et utilisent une méthode simple de consensus pour prendre la décision finale (vote, ou moyenne des prédictions)
• StackingClassifier & Stacking Regressor: ils implémentent le stacking à une seule couche avec une validation croisée pour l'entrainement du modele de sortie

from sklearn.ensemble import StackingClassifier
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from sklearn.linear_model import LogisticRegression

estimators = [
    ('rf', RandomForestClassifier(n_estimators=10, random_state=42)),
    ('svr', make_pipeline(StandardScaler(),
                          LinearSVC(random_state=42)))
]

stacked_model = StackingClassifier(
    estimators=estimators, final_estimator=LogisticRegression(),cv=5)

stacked_model = stacked_model.fit(X_train,y_train)
cv_results = cross_validate(stacked_model, X_train, y_train, cv=5)

print(f"Cross-validated training & score on validation set: {cv_results['test_score'].mean()}")
print(f"Score on test set: {gb.score(X_test,y_test)}")

Cross-validated training & score on validation set: 0.9523809523809523
Score on test set: 0.9881685629476077

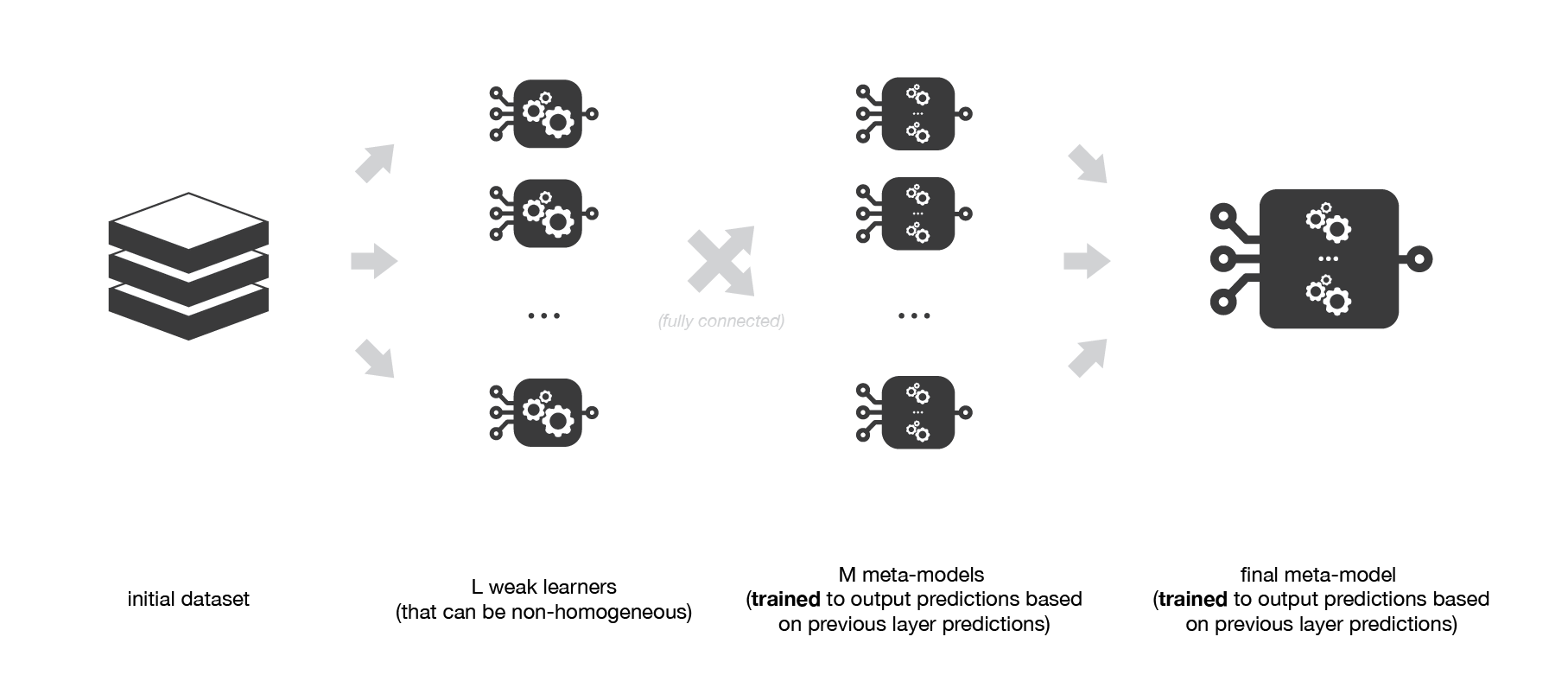
Stacking multi couches

On peut étendre le principe du stacking simple en rajoutant des couches de méta-modèles intermédiaires.
Chacun de ces modèles individuels va s'entrainer en prenant comme entrée les prédictions des modèles individuels de la couche précédante.

d'apres Josep Rocca

Résumé

Bagging	Boosting	Stacking
Modèles individuels homogènes	Modèles individuels homogènes	Modèles individuels hétérogènes
Classification & Régression	Classification & Régression	Classification & Régression
entrainements en parallèle	entrainements séquentiel	parallèle &séquentiel
vise à réduire la variance	vise à réduire le biais
plutôt utilisé avec des arbres de décision profond	plutôt utilisé avec des arbres de décision peu profonds	dépend des modèles individuels
BaggingEstimatorsRandomForest,	Adaboost	VotingClassifier & VotingRegressor
ExtremelyRandomisedTrees	GradientTreeBoosting	StackingClassifier&StackingClassifier
	XBoost,LightGBM,CatBoost

Sources et lectures supplémentaires

• Article du blog towards data science plutôt complet
• Le cours d'Open Classrooms sur les méthodes ensemblistes
• Le gradient boosting expliqué visuellement
• Comparaison des algorithmes, XGBoost, LightGBM & CatBoost