Leçon : Evaluation d'un modèle

Les métriques d'évaluation

Les métriques d'évaluation servent à quantifier la performance d'un modèle (une fois qu'il est entrainé) pour un problème donné, et ce tout au long du cycle de vie d'un modèle.

from sklearn import metrics

Attention !

Les métriques sont à choisir en fonction des caractéristiques de la tâche: classification, régression, clustering ...

Une métrique seule ne vous donne qu'un point de vue partiel de la performance d'un modèle pour une tâche : il est souvent souhaitable de comparer différentes métriques d'évaluation

De plus, la métrique ne vous donne pas nécessairement d'information concernant son interprétabilité, il convient d'inspecter son modèle par des analyses complémentaires comme à l'analyse des relations entre la variable de réponse et les features, ou des relations entre les features entre elles.

Aucun modèle ne peut avoir les meilleurs performances pour toutes les tâches (No Free Lunch Theorem) !

Score de référence (baseline)

Il convient de toujours de calculer le score d'un modèle de référence pour servir de point de comparaison à votre métrique d'évaluation !

Il peut s'agir d'un résultat provenant de l'état de l'art du domaine étudié, par exemple:

• un modèle physique pour la prédiction du réchauffement climatique
• la performance d'un humain sur la même tache

Ou sinon d'un modèle stupide donnant une réponse stéréotypée, par exemple:

• donner une réponse aléaroire
• pour la classification: prédire la classe la plus fréquente
• pour la régression: prédire une mesure de tendance centrale (moyenne, médiane, mode)
• ...

Exemple de modèle baseline stupide avec sklearn

DummyClassifier pour les classifieurs :

import numpy as np
from sklearn.dummy import DummyClassifier
X = np.array([-1, 1, 1, 1])
y = np.array([0, 1, 1, 1])

dummy_clf = DummyClassifier(strategy="most_frequent")
dummy_clf.fit(X, y)

dummy_clf.predict(X)

dummy_clf.score(X, y)

0.75

DummyClassifier pour les regresseurs :

import numpy as np
from sklearn.dummy import DummyRegressor
X = np.array([1.0, 2.0, 3.0, 4.0])
y = np.array([2.0, 3.0, 5.0, 10.0])

dummy_regr = DummyRegressor(strategy="mean")
dummy_regr.fit(X, y)

dummy_regr.predict(X)

dummy_regr.score(X, y)

0.0

Métriques de régression courantes

Exemple de data set pour la régression

Ce data set mesure la nombre de locations de vélo en fonction de certaines environnementales variables comme la météo :

from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split

bikes = fetch_openml("Bike_Sharing_Demand", version=2, as_frame=True, parser='auto')

bikes.data.head()

	season	year	month	hour	holiday	weekday	workingday	weather	temp	feel_temp	humidity	windspeed
0	spring	0	1	0	False	6	False	clear	9.84	14.395	0.81	0.0
1	spring	0	1	1	False	6	False	clear	9.02	13.635	0.80	0.0
2	spring	0	1	2	False	6	False	clear	9.02	13.635	0.80	0.0
3	spring	0	1	3	False	6	False	clear	9.84	14.395	0.75	0.0
4	spring	0	1	4	False	6	False	clear	9.84	14.395	0.75	0.0

bikes.target.head()

0    16
1    40
2    32
3    13
4     1
Name: count, dtype: int64

Methode hold out

# Make an explicit copy to avoid "SettingWithCopyWarning" from pandas
X, y = bikes.data.copy(), bikes.target
# Split the data into a training set and a test set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

Préparation minimale : scaling des features numériques & encoding des features catégorielles

numerical_features = [
    "temp",
    "feel_temp",
    "humidity",
    "windspeed",
]
categorical_features = X_train.columns.drop(numerical_features)

from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder, QuantileTransformer

mlp_preprocessor = ColumnTransformer(
    transformers=[
        ("num", QuantileTransformer(n_quantiles=100), numerical_features),
        ("cat", OneHotEncoder(handle_unknown="ignore"), categorical_features),
    ]
)
mlp_preprocessor

ColumnTransformer(transformers=[('num', QuantileTransformer(n_quantiles=100),
                                 ['temp', 'feel_temp', 'humidity',
                                  'windspeed']),
                                ('cat', OneHotEncoder(handle_unknown='ignore'),
                                 Index(['season', 'year', 'month', 'hour', 'holiday', 'weekday', 'workingday',
       'weather'],
      dtype='object'))])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Entrainement d'un modèle : MLP Regressor

from sklearn.neural_network import MLPRegressor
from sklearn.pipeline import make_pipeline

print("Training MLPRegressor...")
mlp_model = make_pipeline(
    mlp_preprocessor,
    MLPRegressor(
        hidden_layer_sizes=(30, 15),
        learning_rate_init=0.01,
        early_stopping=True,
        random_state=0,
    ),
)
mlp_model.fit(X_train, y_train)

Training MLPRegressor...

Pipeline(steps=[('columntransformer',
                 ColumnTransformer(transformers=[('num',
                                                  QuantileTransformer(n_quantiles=100),
                                                  ['temp', 'feel_temp',
                                                   'humidity', 'windspeed']),
                                                 ('cat',
                                                  OneHotEncoder(handle_unknown='ignore'),
                                                  Index(['season', 'year', 'month', 'hour', 'holiday', 'weekday', 'workingday',
       'weather'],
      dtype='object'))])),
                ('mlpregressor',
                 MLPRegressor(early_stopping=True, hidden_layer_sizes=(30, 15),
                              learning_rate_init=0.01, random_state=0))])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Mean Squared Error (MSE)

Elle mesure la différence quadratique moyenne entre les labels $y$ et leurs valeur prédites $\hat y$ :

$$MSE = \frac{1}{n}\sum_{i=1}^n(y_i - \hat y_i)^2$$

Quelques une de ses caractéristiques:

• utile pour pénaliser les erreurs importantes
• très sensible aux outliers
• ne donne pas la direction de l'erreur
• ne donne pas le même ordre de grandeur que $y$

Root Mean Squared Error (MSE)

$$ RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^n(y_i - \hat y_i)^2}$$

L'utilisation de la racine carrée permet d'avoir une erreur de même ordre de grandeur que les labels

Mean Absolute Error (MAE)

Elle mesure la moyenne de la différence absolue (norme $L_1$) entre les labels $y$ et leurs valeur prédites $\hat y$ :

$$MAE = \frac{1}{n}\sum_{i=1}^n |y_i - \hat y_i|$$

Elle est moins sensible aux outliers, utilisez la si les erreurs (petites ou grandes) ont la même importance

Max Error

Elle mesure la plus grande erreur faite par le modèle:

$$ME = max{_{i=1}^n|y_i - \hat y_i|}$$

Utilisez Max error lorsque vous souhaitez limiter la magnitude des erreurs

Le coefficient de détermination $R^2$

Mesure la proportion de variance observée sur $y$ qui est expliquée par les variables $X$ du dataset. Elle évalue la qualité de l'ajustement du modèle (goodness of fit) par rapport à un modèle stupide qui prédirait toujours $\bar y$

$$R^2(y,\hat y) = 1 - \frac{\sum{_{i=1}^n} (y_i-\hat y_i)^2}{\sum{_{i=1}^n} (y_i-\bar y_i)^2} $$

• $R^2$ = 1 caratérise modèle qui ajuste parfaitement les données
• $R^2$ ~ 0 caractéirse un modèle qui ne fait pas mieux que le modèle stupide
• $R^2$ < 0 caractérise un modèle plus mauvais encore !

Quelques une de ses caractéristiques:

• donne une mesure d'erreur standardisée (entre -1 et 1)
• peux être utilisée pour comparer la performance d'un modèle sur différents data set

Exemples de comparaison de métrique durant la cross-validation

from sklearn.model_selection import cross_validate

cv_results = cross_validate(mlp_model, X_train, y_train, cv=5, 
                            scoring = ['neg_mean_absolute_error',
                                       'neg_mean_squared_error',
                                       'max_error','r2'])

pd.DataFrame(cv_results)

	fit_time	score_time	test_neg_mean_absolute_error	test_neg_mean_squared_error	test_max_error	test_r2
0	1.698149	0.010826	-30.098396	-2280.340766	-360.056151	0.929707
1	5.293706	0.020174	-28.083844	-1998.342875	-463.954552	0.939888
2	4.315770	0.013060	-27.319143	-1836.767237	-271.759472	0.942871
3	3.086931	0.009863	-28.370111	-2141.842609	-443.785465	0.936017
4	3.279214	0.011184	-27.561188	-1887.310100	-364.704323	0.942186

cv_results['test_r2'].mean()

0.938133980593818

Métrique de classification courantes

On distingue souvent 3 types de classification: binaire {$C_0$,$C_1$}, multiclasse {$C_1 \ldots C_n $}, et mutlilabel { {$C_1$,$D_1$},$\ldots$,$C_n$,$D_n$} }

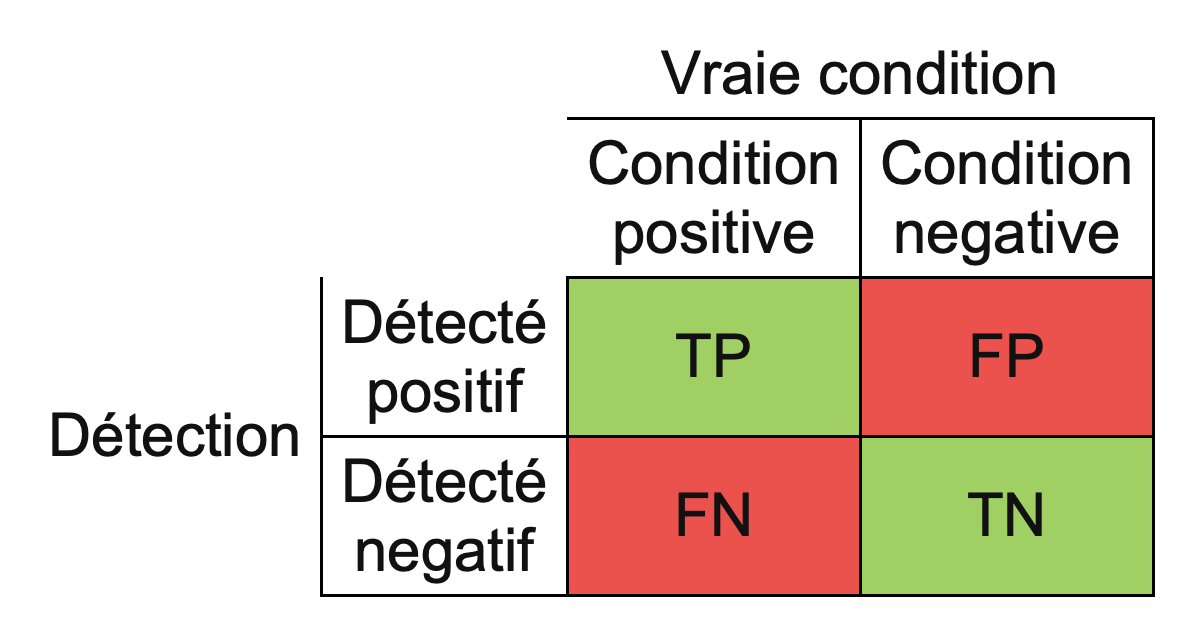
Matrice de confusion

Dans les tâches de classification, on distingue souvent deux types d'erreurs, que l'on peut représenter par une matrice de confusion

Exemple de matrice de confusion pour une classification multiclasse

on entraine un SVC sur le très connu iris data set:

import matplotlib.pyplot as plt

from sklearn import svm, datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import ConfusionMatrixDisplay

# import some data to play with
iris = datasets.load_iris()
X = iris.data
y = iris.target
class_names = iris.target_names

# Split the data into a training set and a test set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# Run classifier, using a model that is too regularized (C too low) to see
# the impact on the results
classifier = svm.SVC(kernel="linear", C=0.01).fit(X_train, y_train)

On représente souvent la matrice de confusion sous forme de carte de chaleur:

confmat = ConfusionMatrixDisplay.from_estimator(
        classifier,
        X_test,
        y_test,
        display_labels=class_names,
        cmap=plt.cm.Blues,
)
confmat.ax_.set_title("Confusion matrix");

Beaucoup de métriques de classification se basent sur la matrice de confusion ! (voir la page wikipédia dédiée pour plus de détails)

Accuracy score

C'est le score le plus simple, il correspond à la fraction de réponses correcte:

$$ accuracy = \frac{TP + TN}{TP + TN + FP +FN} $$

Attention ! C'est une mesure qui donne un score trop confiant en particulier lorsque le dataset à traiter contient des classes déséquilibrées, on lui préfera le balanced accuracy score dans ce cas

Balanced accuracy score

$$ balanced~accuracy = \frac{1}{2}(\frac{TP}{TP + FN} + \frac{TN}{TN + FP})$$

Recall / sensitivity / true positive rate

Cette métrique mesure la capacité du classifieur à détecter les vrais positifs parmi les échantillons positifs:

$$ recall = \frac{TP}{TP + FN}$$

On utilise de préférence le recall lorsqu'il est important d'identifier les occurences d'une classe, par exemple pour un test de dépistage d'une maladie

Precision

Cette métrique mesure la capacité du classifieur à détecter les vrais positifs parmi les prédictions positives:

$$ precision = \frac{TP}{TP + FP}$$

On utilise de préférence la précision lorsqu'il est important d'identifier correctement une classe, par exemple lorsque l'on utilise un moteur de recherche

F-score

Il s'agit d'une métrique combinant, avec un poids, la précision et le recall. On utilise souvent le F1 score :

$$ F_1 = 2\frac{precision.recall}{precision + recall}$$

mais on peut généraliser la pondération avec n'importe quelle valeur:

$$ F_\beta = (1+\beta^2)\frac{precision.recall}{\beta^2precision + recall}$$

• le meilleur score de $F_\beta$ vaut 1, le pire score 0
• donne le même poids au recall et la précision, si $\beta > 1$ on favorise le recall

Classification report

Cette fonction de scikit-learn renvoie un rapport intégrant plusieurs métriques de classification:

• la précision
• le recall
• le F1-score
• le support (le nombre de points utilisés)

from sklearn.metrics import classification_report

print(classification_report(y_test,classifier.predict(X_test) , target_names=class_names))

              precision    recall  f1-score   support

      setosa       1.00      1.00      1.00        13
  versicolor       1.00      0.62      0.77        16
   virginica       0.60      1.00      0.75         9

    accuracy                           0.84        38
   macro avg       0.87      0.88      0.84        38
weighted avg       0.91      0.84      0.84        38

Specificity / selectivity / true negative rate

Cette métrique mesure la capacité du classifieur à détecter les vrais négatifs parmi les échantillons négatifs:

$$ specificity = \frac{TN}{FP + TN}$$

ROC curve area (AUC)

La courbe ROC (Receiver Operating Characteristic) est une mesure de la performance d'un classifieur binaire, qui provient de la théorie de la détection du signal (elle etait utilisée pour séparer les signaux radar du bruit de fond)

Pratiquement, elle est calculée en faisant calculant le True positive rate (ou sensitivity) versus le True negative rate (1-specificity) en faisant varier un seuil de discrimination. La métrique consiste alors à mesurer l'aire sous la courve ROC (AUC) comme score

Pour en avoir un exemple interactif pour comprendre sa construction, consulter ce site

Métriques multilabel

Bien que certaines des métriques présentées peuvent avoir des variantes multilabel, il existe des métriques spécifiques aux tâches de classification multilabel (qui consistent à prédire plusieurs labels en même temps)

Certaines d'entre elles sont décrites et implémentées dans scikit-learn comme la coverage error, label ranking average precision, la ranking loss, ...

Métriques de clustering

Métriques nécessitant la connaissance de labels

La plupart des métriques d'évalutation du clustering nécessitent la connaissance à priori de labels

Comment se fait il, me direz vous ? l'apprentissage non supervisé n'est-il pas sensé se faire sans la connaissance de la target y ? 🤔

Dans la pratique, de nombreux algorithmes de clustering peuvent assigner aux points du dataset un label (le numéro du cluster auquel ils appartiennent). On peut alors utiliser ce label pour calculer la métrique d'évaluation

Le Rand Index

Connaissant l'assignement entre les labels labels_pred assignés à chaque point de donnée par le modèle de clustering et leur label réel label_true, ce type de métrique mesure la similarité entre deux assignements (mesurée entre 0 et 1), en ignorant les permutations

labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
metrics.rand_score(labels_true, labels_pred)

0.6666666666666666

le score ne change pas si on permute uniquement les valeurs des labels:

labels_pred = [1, 1, 0, 0, 3, 3]
metrics.rand_score(labels_true, labels_pred)

0.6666666666666666

Cependant le Rand index n'assure pas d'obtenir une valeur nulle pour une assignation dûe au hasard. l'adjusted Rand Index corrige ce problème en prenant le niveau de chance dû au hasard comme référence

metrics.adjusted_rand_score(labels_true, labels_pred)

0.24242424242424243

Les métrique de type Information Mutuelle

Ce type de métriques provient de la théorie de l'information. Elle mesure l'information mutuelle, c.a.d l'agrément entre les labels labels_pred assignés à chaque point de donnée par le modèle de clustering et leur label réel label_true

Par exemple, l'Adjusted MutualInformation qui prend en compte le hasard, renvoie un score compris entre 0 (pour deux partition assignée dont on aurait assigné les labels au hasard) et 1 pour deux partitions parfaitement identiques

labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]

metrics.adjusted_mutual_info_score(labels_true, labels_pred)  

0.2987924581708901

Quelques métriques agnostique des labels

Contrairement aux métriques présentées plus tôt, certaines métriques de clustering ne nécessitent pas la connaissance d'un label label_true.

Intuitivement elles vont s'appuyer sur une évaluation de l'homogeneité des clusters produits

Le score de silhouette

Le score de silhouette est une métrique basée sur la distance entre un points et tout ceux d'un même cluster, en comparaison avec tout ceux du cluster le plus proche.

Il se base sur deux scores :

• a : la distance moyenne entre un point et les autres points du même cluster
• b: la distance moyenne entre un point et les autres points du cluster voisin le plus proche

$$s = \frac{b-a}{max(a,b)}$$

Il varie entre -1, indiquant un clusterting fortement incorrect et 1 pour des clusters très dense et distincts les uns des autres,

Exemple avec un K-means appliqué au data set iris:

from sklearn import datasets
X, y = datasets.load_iris(return_X_y=True)

from sklearn.cluster import KMeans
kmeans_model = KMeans(n_clusters=3, random_state=42, n_init='auto').fit(X_train)
labels = kmeans_model.labels_

metrics.silhouette_score(X_train, labels, metric='euclidean')

0.5618512101716054

L'index de Calinski-Harabasz

Il s'agit d'une métrique basée sur le ratio entre; la somme de la dispersion intra-clusters et celle inter-clusters

Cette métrique n'est pas normalisée et donne en général un nombre réel positif, d'autant plus grand que les clusters sont disjoints et homogènes :

metrics.calinski_harabasz_score(X_train, labels)

433.0933726899339

L'index de Davies-Bouldin

Il s'agit d'une métrique basée sur la similarité moyenne entre les clusters (mesurée par le ratio de la distance intra-clusters à celle inter-clusters)

Le score minimum est zéro, un score faible indiquant un clustering de meilleure qualité

from sklearn.metrics import davies_bouldin_score
davies_bouldin_score(X_train, labels)

0.6402727236753957

Analyse des relations entre variables

Utiliser une ou plusieurs métriques est un premier pas, mais ne suffit pas à comprendre les relations entre les variables et leurs impacts sur les prédictions.

Analyse des relations entre features

Il s'agit d'analyser les relations entre les features, par exemple en examinant l'importance des features utilisée par le modèle.

Certains modèles possèdent nativement un tel score :

• les coefficients d'une régression
• l'importance des features utilisées dans les partition d'un arbre de décision

La plupart des modèles n'ayant pas de score natifs, on peut utiliser des méthodes génériques:

• l'importance des features calculées par permutation (en particulier pour les modèles non linéaires sur des données tabulaires)
• des modules dédiés proposent des methodes de calcul d'importance des features, commeLIME ou SHAP

Analyse des relations entre features et variable cible

Il s'agit d'analyser les relations entre les prédicteurs et variables cibles, en particulier leur degré de dépendance

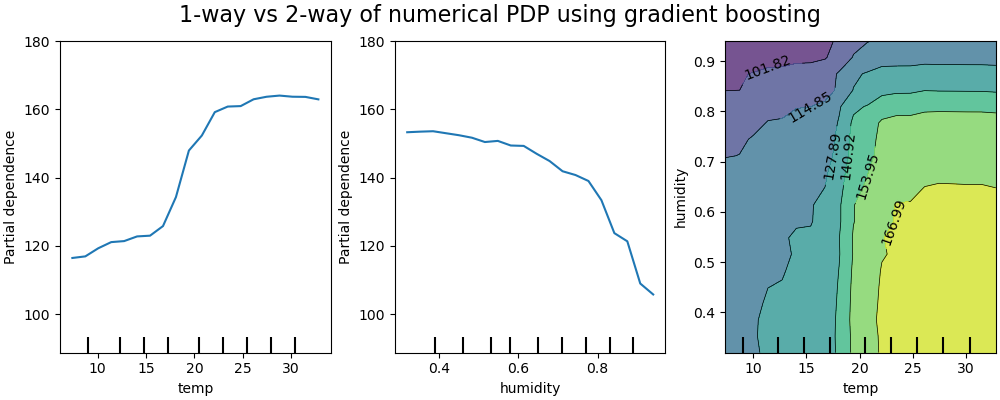
Analyse de dépendance partielle (partial dependence plots - PDP)

On utilise souvent les graphiques PDP pour représenter la dépendance de la variable de réponse, avec un sous groupe de features d'intérêt (généralement un petit nombre parmi les plus importantes), en comparaison avec toutes les autres features

Exemple de PDP sur un modèle de prédiction de la location de vélo avec les variables température et humidité

d'apres scikit-learn

Individidual conditional expectation plot (ICE)

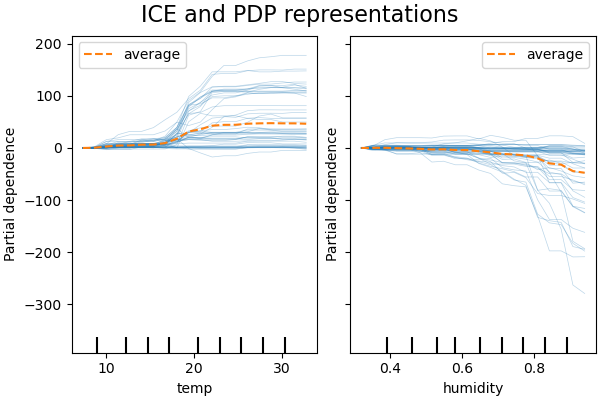
l'ICE représente la dépendance entre la variable de réponse et un sous groupe de features représentatif, pour chaque obervation séparément. On représente généralement une feature d'intrêt par grapique d'ICE (pour faciliter sa lecture)

Exemple d'ICE sur le même modèle de prédiction de location de vélo:

d'apres scikit-learn

Pour plus de détails sur l'analyse de dépendence partielle des variables de ce data set, vous pouvez voir l'exemple complet sur scikit-learn