Leçon : Algèbre linéaire pour la data science

L'algèbre linéaire pour la data science

L'algèbre linéaire est une branche des mathématiques qui étudie les espaces vectoriels et les transformations qu'on peut leur appliquer

Pratiquement, l'algèbre linéaire en data science nous est utile pour certains concepts comme:

• encoder tout type de données en une représentation numérique efficace pour les calculs
• faire des calculs sur des vecteurs, matrices, et plus généralement des tenseurs
• calculer des décompositons de matrices comme les valeurs propres et vecteurs propres
• calculer des nouveaux espaces de représentation pour notre data set (par rapport à l'espace de représentation de départ)
• transformer des systèmes d'équations en équations vectorielles
• ...

Notion d'espace vectoriel

Définition résumée

Basiquement, il s'agit d'un ensemble muni de deux lois de compositions (additive et multiplicative), lois permettent de réaliser des opérations sur les éléments de cet ensemble (et dont le résultat donne nécéssairement des éléments appartenant à cet ensemble).

(Attention : j'ai passé sous silence certaines propriétés supplémentaires nécessaires pour définir définir rigoureusement les espaces vectoriels)

Représentation graphique

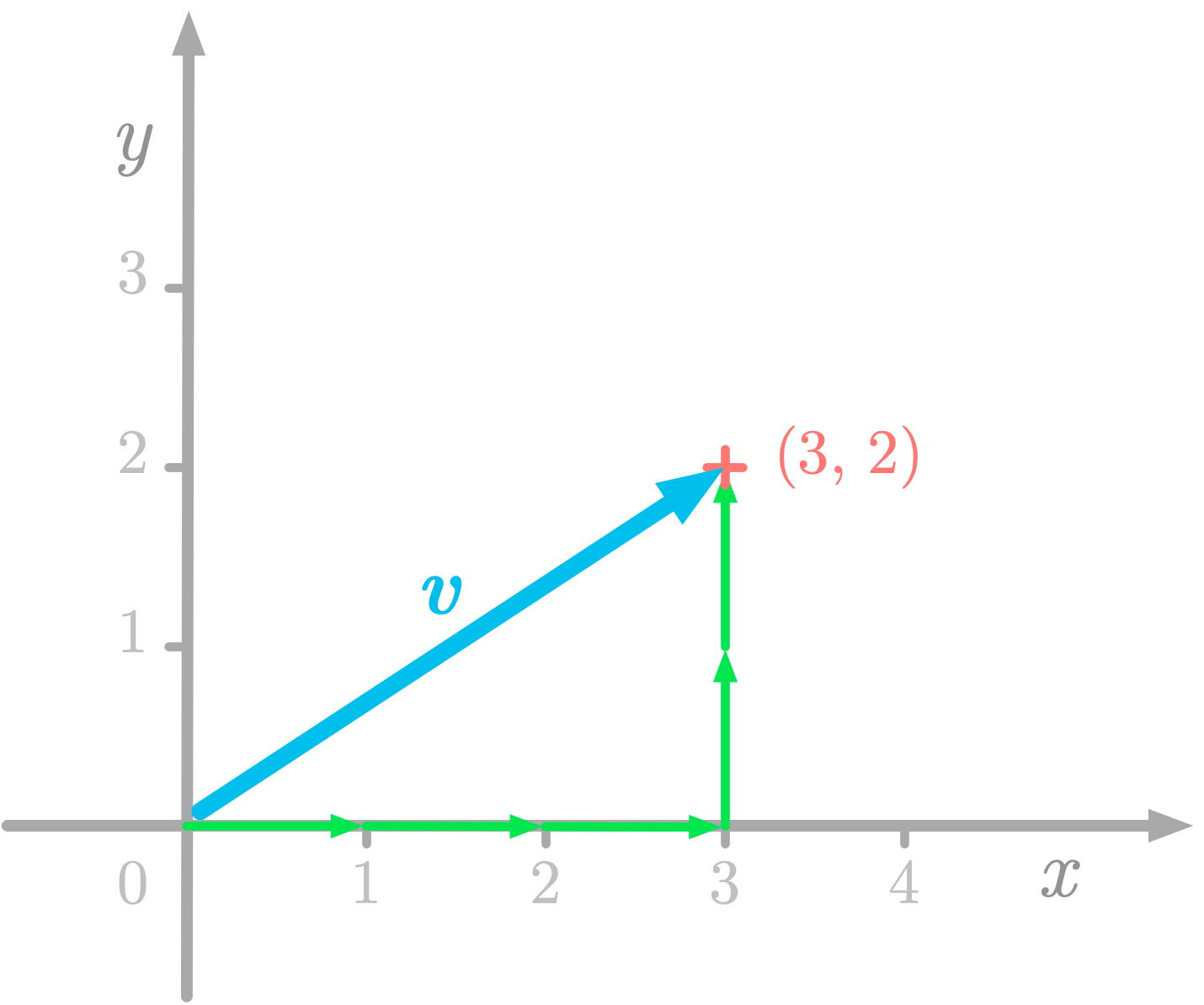
Les éléments d'un espace vectoriels sont des vecteurs, dont chacun peut se décomposer comme une combinaison linéaire de vecteurs de base, comme dans ce repère orthonormé (une base de vecteurs orthogonaux):

D'après Hadrien Jean

Dans cet exemple, on a: $$v = 3i + 2j$$

Notion de vecteurs

Annotations de présentation

• on peut faire des vecteurs avec n'importe quelle entitée
• notation sous forme de square braquet
• on peut les représenter comme des fleches au centre d'un repère qui donne les coordonnées de n'importe qu'elle point
• montrer comment on peut construire une espace vectoriel
• somme de vecteurs (schéma + opération +ex)
• mutliplication de vecteurs
• multiplication par un nb (montrer des exemples et expliquer la notion de scaler)

Intuition

Une manière simple de concevoir les vecteurs est une "flèche" donnant les coordonnées d'un point dans un sytème de coordonnées, souvent un repère

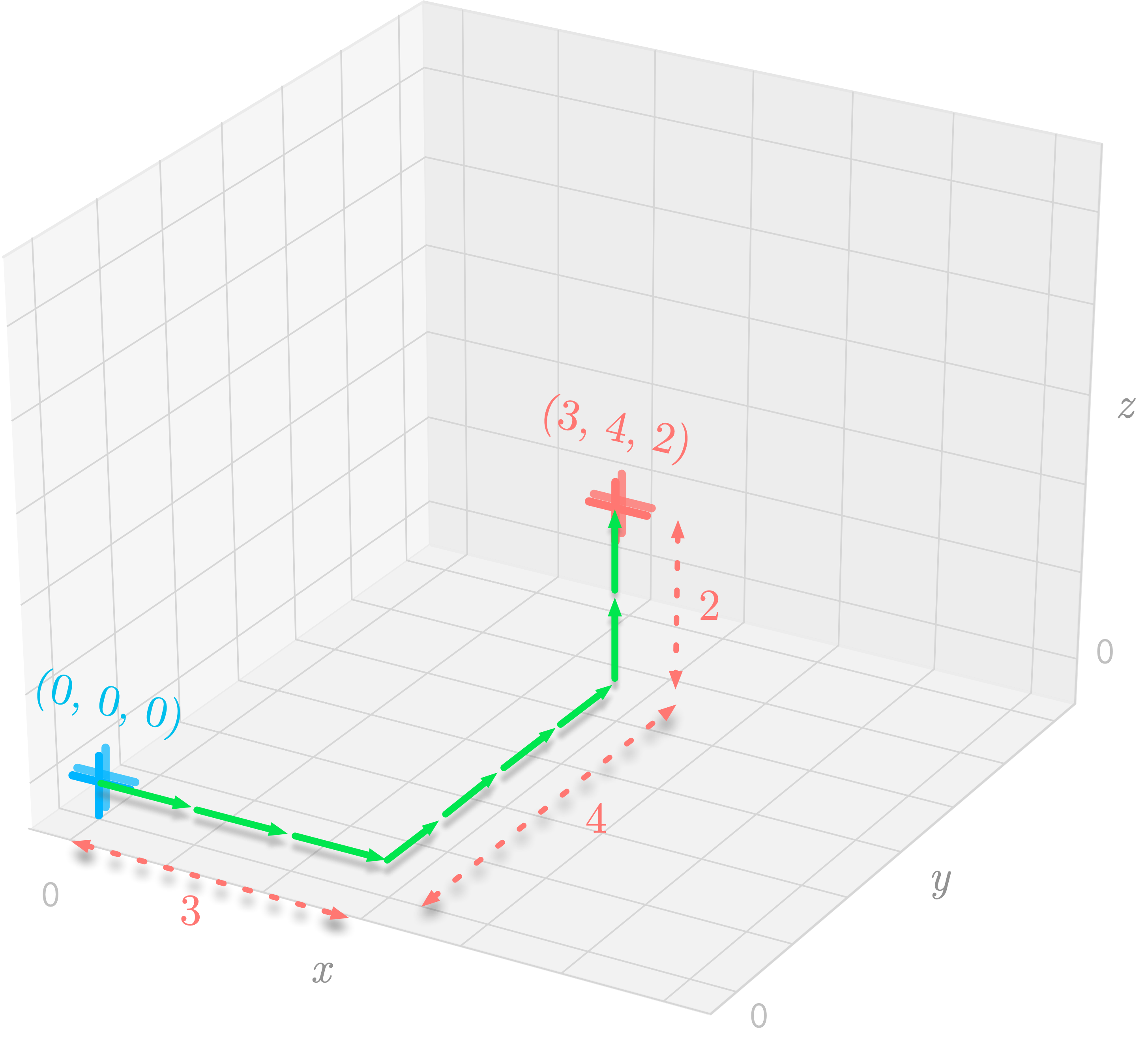
Dans ce syteme de coordonnée, chaque point peut être représenté par un vecteur, comme ici dans un espace vectoriel à 2-dimensions:

D'après Hadrien Jean

... ou encore à dans un espace vectoriel à 3 dimensions:

D'après Hadrien Jean

La notion de base et de vecteurs de base

Mathématiquement, un vecteur est un point dans un espace vectoriel et peut s'écrire comme une combinaison de vecteur de base. L'ensemble de ces vecteurs, associé à un point d'origine, forme un repère

En algèbre linéaire, chaque vecteur ou point, se décompose comme une combinaison linéaire de vecteurs de base, par exemple :

$$v = \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} = a_1 \begin{bmatrix} 1 \\ 0 \\ 0\end{bmatrix} + a_2 \begin{bmatrix} 0 \\ 1 \\ 0\end{bmatrix} + a_3\begin{bmatrix} 0 \\ 0 \\ 1\end{bmatrix} $$

Ecriture mathématique et informatique

En data science, un vecteur est utilisé pour encoder un objet sous forme de valeurs numériques. Très souvent, il sert à représenter les valeurs numériques d'un data set comme une collection de vecteurs.

Vecteur ligne

un vecteur ligne, représente un échantillon de données, dans laquelle chaque composante correspond à la même observation de différentes variable

$$ v = \begin{bmatrix} 3 & 4 & 2 \end{bmatrix}$$

v = np.array([3,4,5])
v

array([3, 4, 5])

Vecteur colonne

un vecteur colonne, représentant une variable ou feature, dans laquelle chaque composante correspond à une observation de cette variable.

$$ v = \begin{bmatrix} 3 \\ 4 \\ 2 \end{bmatrix}$$

v = np.array([3,4,2])
v.reshape(3,1)

array([[3],
       [4],
       [2]])

Généralisation à n dimensions

Plus généralement, les vecteurs peuvent avoir $n$ composantes lorsqu'ils représentent des points dans un espace a $n$ dimensions, par exemple des nombres réels $\mathbb{R}^n$

$$ v = \begin{bmatrix} 3 \\ 4 \\ 2 \\ \vdots \\ n \\ \end{bmatrix}$$

C'est une représentation efficace pour les vecteurs en géométrie euclidienne, mais on peut généraliser ce concept à différents objets : on peut construire des vecteurs représentant des mots, des fonctions mathématiques, ...

Opérations sur les vecteurs

Multiplication par un scalaire k

Si $v = \begin{bmatrix} 3 \\ 2\end{bmatrix}$ alors $kv = \begin{bmatrix} k*3 \\ k*2\end{bmatrix}$

v = np.array([3,2])
v

array([3, 2])

5*v

array([15, 10])

Produit scalaire (dot product)

Il multiplie deux vecteurs pour donner un scalaire, suivant la formule:

$$u.v = \sum_{i=1}^{m} u_iv_i$$

$$u.v = \begin{bmatrix} 3 \\ 2 \\ 5\end{bmatrix} . \begin{bmatrix} 7 \\ 1 \\ 3\end{bmatrix} = 3 \times 7 + 2 \times 1 + 5 \times 3 = 38 $$

u = np.array([3,2,5])
v = np.array([7,1,3])
np.dot(u,v)

38

Norme d'un vecteur

La norme d'un vecteur est un scalaire, résultat de son produit scalaire par lui même. Par exemple la norme euclidienne, $L_2$ : $${\parallel u \parallel}_2^2 = u.u$$

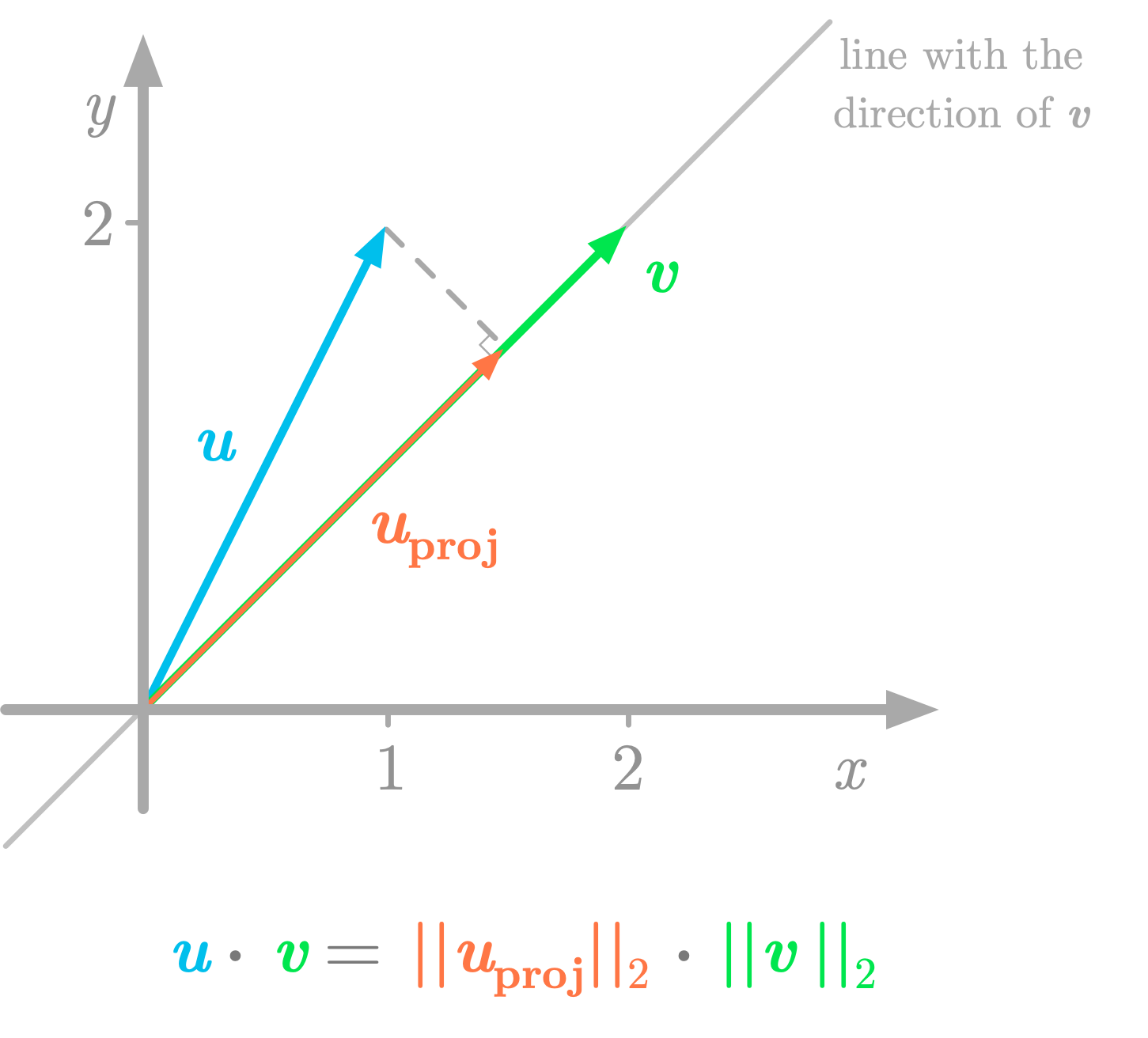
Interprétation géométrique

La multiplication de deux vecteurs $u = \begin{bmatrix} 1 \\ 2\end{bmatrix}$ et $v = \begin{bmatrix} 2 \\ 2\end{bmatrix}$ s'interpète comme la multiplication vectorielle de la norme de v par celle de la projection de u sur v:

D'après Hadrien Jean

A ne pas confondre avec le produit vectoriel (vector multiplication)

$$u\odot v = \begin{bmatrix} 3 \\ 2 \\ 5\end{bmatrix} \odot \begin{bmatrix} 7 \\ 1 \\ 3\end{bmatrix} = \begin{bmatrix} 3 . 7 \\ 2 . 1\\ 5 . 3\end{bmatrix} = \begin{bmatrix} 21 \\ 2 \\ 15\end{bmatrix} $$

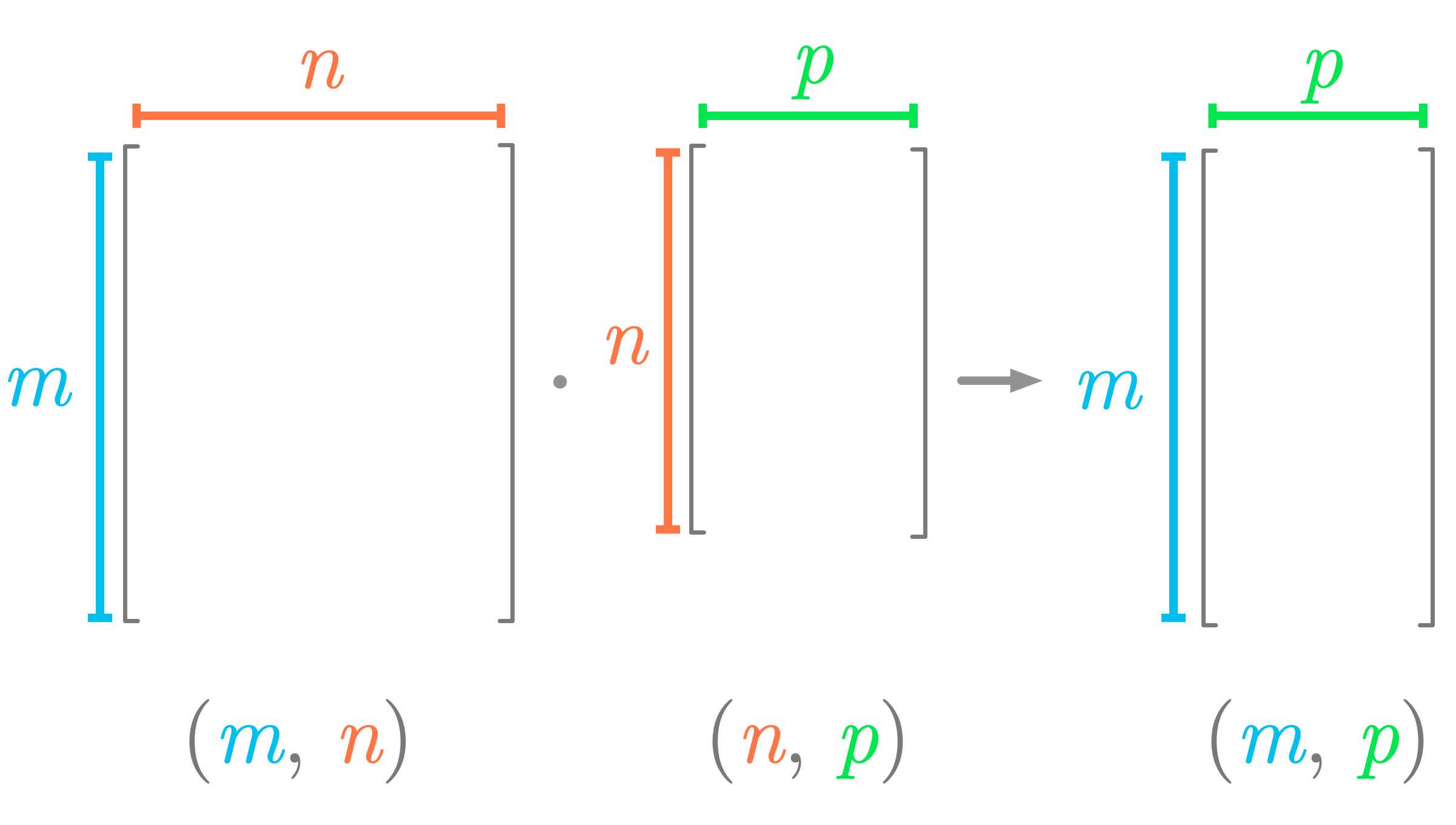
Les matrices et tenseurs

Définition résumée

En data science, on peut voir une matrice comme une structure de données sous forme de tableau. On représentera souvent ces deux dimensions comme :

• les observations (en ligne)
• les variables (en colonne)

Par exemple, on pourrait écrire une matrice de données $X$ de dimension $(n,p)$ :

$$ X = \begin{bmatrix} X_{1,1} & X_{1,2} & \dots & X_{1,p} \\ X_{2,1} & X_{2,2} & \dots & X_{2,p} \\ \dots & \dots & \dots & \dots \\ X_{n,1} & X_{n,2} & \dots & X_{n,p} \\ \end{bmatrix}$$

Les matrices : des cas particuliers de tenseurs

Plus généralement, les matrices sont des cas particuliers d'objets mathématiques appelés les tenseurs:

• Un scalaire est un tenseur d'ordre 0
• Un vecteur un tenseur d'ordre 1
• Une matrice un tenseur d'ordre 2
• ...

En data science, les matrices nous seront particulièrement utiles pour représenter des transformations (en particulier celle linéaire) et également écrire des systèmes d'équation de manières factorisée

représentation avec numpy

On peut facilement utiliser toutes les propriétés des matrices avec numpy :

X = np.array([[2.1, 7.9, 8.4],
              [3.0, 4.5, 2.3],
              [12.2, 6.6, 8.9],
              [1.8, 1.3, 8.2]])

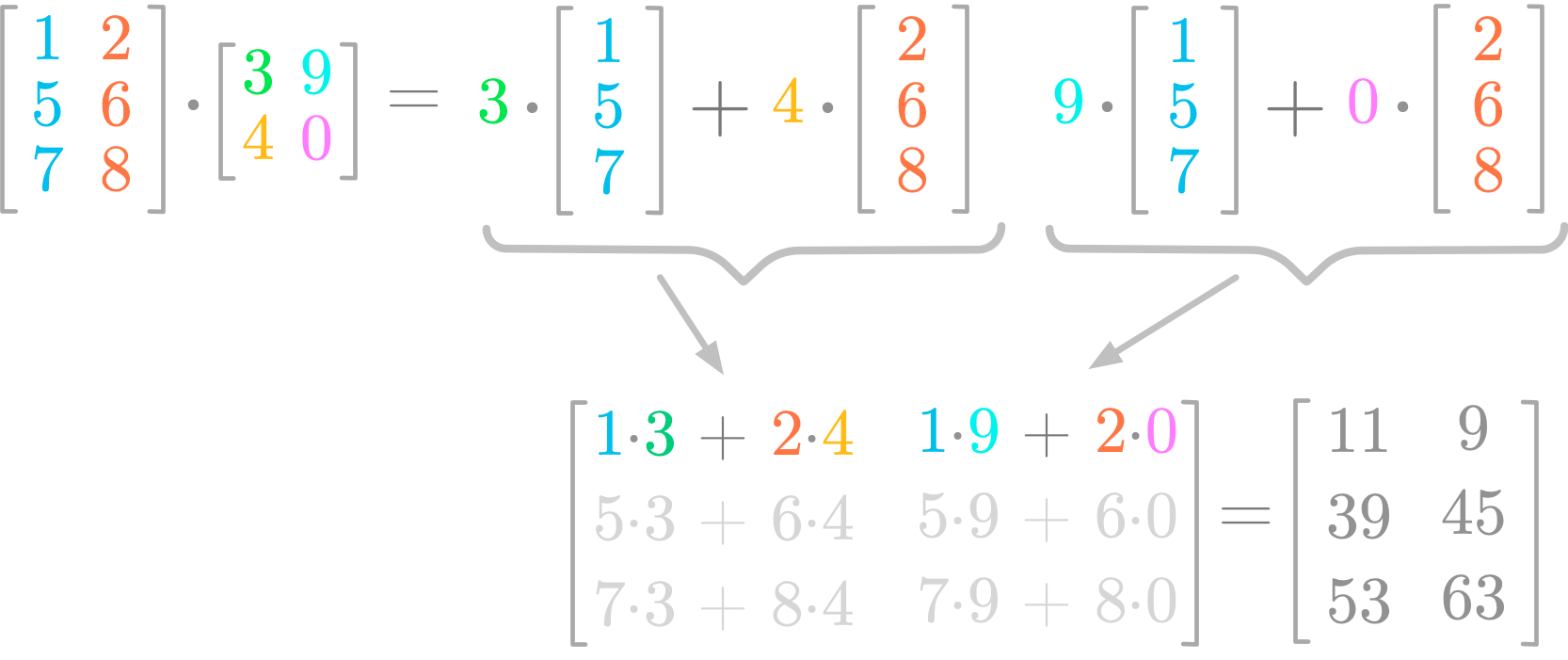
Produit de matrices

Exemple de calcul

Il s'agit d'une opération très courante en algèbre linéaire. La multiplication d'une matrice $A$ par $B$ donne une matrice, suivant le schéma suivant :

D'après Hadrien Jean

Avec numpy

A = np.array([
    [1, 2],
    [5, 6],
    [7, 8],
])
B = np.array([
    [3, 9],
    [4, 0]
])

np.dot(A,B) # On peut aussi écrire A @ B

array([[11,  9],
       [39, 45],
       [53, 63]])

Attention au dimensions des matrices

Attention, pour pouvoir réaliser un produit deux matrices, celle-ci doivent avoir des dimensions compatibles !

D'après Hadrien Jean

Pour plus de détails concernant les propriétés du produit matriciel, voire cette page dédiée d'Hadrien Jean

La transposée d'une matrice

C'est une transformation qui consiste à échanger les lignes et les colonnes d'une matrice. On note $A^T$ la matrice transposée de A

X = np.array([[2.1, 7.9, 8.4],
              [3.0, 4.5, 2.3],
              [12.2, 6.6, 8.9],
              [1.8, 1.3, 8.2]])
X

array([[ 2.1,  7.9,  8.4],
       [ 3. ,  4.5,  2.3],
       [12.2,  6.6,  8.9],
       [ 1.8,  1.3,  8.2]])

X.T

array([[ 2.1,  3. , 12.2,  1.8],
       [ 7.9,  4.5,  6.6,  1.3],
       [ 8.4,  2.3,  8.9,  8.2]])

Autres opérations sur les matrices

Certaines opérations plus avancées sont également très utiles en data science :

• la trace d'une matrice
• l'inverse d'une matrice et le pseudo-inverse de Moore-Penrose
• le déterminant
• ...

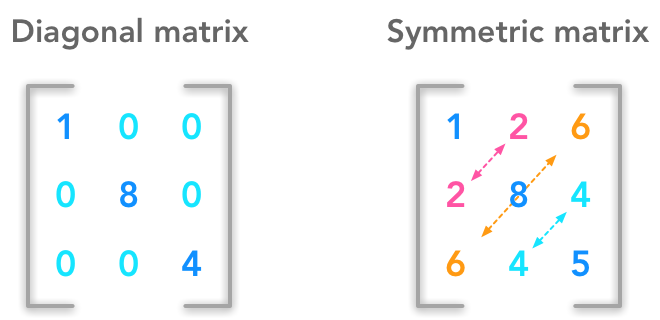
Quelques matrices caractéristiques

La matrice identité

C'est une matrice qui ne contient que des 1 sur sa diagonale, 0 ailleurs

\begin{bmatrix} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \dots & \dots & \dots & \dots \\ 0 & 0 & \dots & 1 \\ \end{bmatrix}

Les matrices diagonales et symétriques

D'après Hadrien Jean

Ces matrices sont intéressantes car elles ont des propriétés qui simplifient certaines formules et calculs dans lesquelles elle sont impliquées

Les matrices comme représentation de transformations linéaires

En plus de la vision de structure tabulaire de données, mathématiquement n'importe quelle transformation linéaire (addition et multiplication par un scalaire) peut se représenter par une matrice

Ainsi, chaque colonne d'une matrice représente la transformation d'un vecteur $T(v)$ d'un vecteur $v$ d'un espace donné:

$$ \begin{array}{c} \begin{matrix} T(e_1) & T(e_2) & \dots & T(e_p)\\ \end{matrix} \\ \begin{bmatrix} X_{1,1} & X_{1,2} & \dots & X_{1,p} \\ X_{2,1} & X_{2,2} & \dots & X_{2,p} \\ \dots & \dots & \dots & \dots \\ X_{n,1} & X_{n,2} & \dots & X_{n,p} \\ \end{bmatrix} \end{array} $$

Une matrice permet ainsi de transformer un espace vectoriel de départ en espace vectoriel d'arrivée !

Exemple de transformation d'un vecteur

Prenons, la transformation d'un vecteur quelquoncque, $v_1$ :

$$ v1 = T(e_1) = T(X_{1,1}.e_1 + X_{2,1}.e_2 + \dots + X_{n,1}.e_p)$$

Si $T$ est une transformation linéaire, on peut écrire :

$$ = T(X_{1,1}.e_1) + T(X_{2,1}.e_2) + \dots + T(X_{n,1}.e_p)$$

$$ = X_{1,1}.T(e_1) + X_{2,1}.T(e_2) + \dots + X_{n,1}.T(e_p))$$

$$ = \begin{bmatrix} T(e_1) & T(e_2) & \dots & T(e_p) \end{bmatrix} \begin{bmatrix} X_{1,1} \\ X_{2,1} \\ \dots \\ X_{n,1} \end{bmatrix} $$

En résumé, on voit que la transformation linéaire T de $v_1$ se décompose comme le produit des nouveaux vecteurs de base $T(e_1), \dots,T(e_n)$ par $v_1$

$$v_1 = \begin{bmatrix} T(e_1) & T(e_2) & \dots & T(e_p) \end{bmatrix} \begin{bmatrix} X_{1,1} \\ X_{2,1} \\ \dots \\ X_{n,1} \end{bmatrix} $$

Interprétation géométrique

Créeons une grille de point dans une espace en 2D. Chaque point de cette grille nous servira a représenter des vecteurs d'un espace vectoriel:

x = np.arange(-10, 10, 1)
y = np.arange(-10, 10, 1)

xx, yy = np.meshgrid(x, y)
plt.scatter(xx, yy, s=20, c=xx+yy);
# the matrix createad this way has a dimension of 20 x 20 = 400 points

Appliquons une transformation $T$ à cet espace

On veut appliquer une matrice $T$ à cet espace pour visualiser comment elle transforme cet espace : $$ T = \begin{bmatrix} -1 & 0 \\ 0 & -1 \\ \end{bmatrix}$$

T = np.array([
    [-1, 0],
    [0, -1]
])

# To apply T (2,2) to our space we have to reshape it to (2,400)
xy =  np.vstack([xx.flatten(), yy.flatten()])
xy.shape

(2, 400)

# We apply T to our reshaped matrix
trans = T @ xy
trans.shape

(2, 400)

# we reshape back our transformed matrix to the original space shape
xx_transformed = trans[0].reshape(xx.shape)
yy_transformed = trans[1].reshape(yy.shape)
xx_transformed.shape

(20, 20)

Visualisation de la transformation $T$

On visualise le résultat de l'application de T sur notre espace qui correspond a l'application d'une rotation de 90° :

f, axes = plt.subplots(1, 2, figsize=(6, 3))
axes[0].scatter(xx, yy, s=10, c=xx+yy)
axes[1].scatter(xx_transformed, yy_transformed, s=10, c=xx+yy);

Pour plus de détails, voire la page source du blog d'Hadrien Jean

Système d'équation linéaire

Exemple

Considérons le sytème d'équation suivant :

$$ \begin{cases} y = 2x + 1 \\ y = -0.5x +3 \\ \end{cases} $$

Représentation graphique

Ce système peut se représenter graphiquement par deux droites, dont les coordonnées d'intersection sont la solution du système:

x = np.linspace(-2, 2, 100)
y = 2 * x + 1
y1 = -0.5 * x + 3
plt.plot(x, y);
plt.plot(x, y1);
plt.xlabel('x')
plt.ylabel('y')
plt.axhline(2.6, xmax=0.68, linestyle = '--', color='k');
plt.axvline(0.8, ymax=0.68, linestyle = '--', color='k');

solutions du système

Les solutions $x=0.8$ et $y=2.6$ vérifient les coordonnées du sytème:

$$ \begin{cases} \textbf{2.6} = 2 \cdot \textbf{0.8} + 1 \\ \textbf{2.6} = -0.5 \cdot \textbf{0.8} +3 \\ \end{cases} $$

Ecriture matricielle

Notre système d'équation $$ \begin{cases} y - 2x = 1 \\ y + 0.5x = 3 \\ \end{cases} $$

peut se réecrire sous forme matricielle : $$ y \begin{bmatrix} 1 \\ 1 \end{bmatrix} + x \begin{bmatrix} -2 \\ 0.5 \end{bmatrix} = \begin{bmatrix} 1 \\ 3 \end{bmatrix} $$

Interprétation graphique

Avec l'interprétation graphique suivante :

D'après Hadrien Jean

Application : écriture matricielle pour décrire la régression linéaire appliquée à un data set

Pour un data set tabulaire contenant $n$ lignes et $p$ colonnes, la régression linéaire peut s'écrire par un système de $n $ équations :

$\hat y_1 = \theta_0 + \theta_1 x_{1,1} + \theta_2 x_{1,2} + \ldots + \theta_p x_{1,p} + \epsilon= \sum{_{i=0}^p \theta_ix_i}+ \epsilon$

$\hat y_2 = \theta_0 + \theta_1 x_{2,1} + \theta_2 x_{2,2} + \ldots + \theta_p x_{2,p} + \epsilon= \sum{_{i=0}^p \theta_ix_i}+ \epsilon$

$\vdots$

$\hat y_n = \theta_0 + \theta_1 x_{n,1} + \theta_2 x_{n,2} + \ldots + \theta_p x_{n,p} + \epsilon= \sum{_{i=0}^p \theta_ix_i}+ \epsilon$

Ce qui se traduit vectoriellement par :

$$\begin{pmatrix} \hat y_1 \\ \hat y_2 \\ \vdots \\ \hat y_n \end{pmatrix} = \begin{pmatrix} 1 & x_{1,1} & x_{1,2} & \cdots & x_{1,p}\\ 1 & x_{2,1} & x_{2,2} & \cdots & x_{2,p}\\ \vdots & \vdots & \vdots & \vdots & \vdots\\ 1 & x_{n,1} & x_{2,2} & \cdots & x_{n,p}\\ \end{pmatrix} \begin{pmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_{p+1} \end{pmatrix} + \begin{pmatrix} \epsilon \\ \epsilon \\ \vdots \\ \epsilon \end{pmatrix}$$

Application : écriture matricielle pour décrire un réseau de neurone

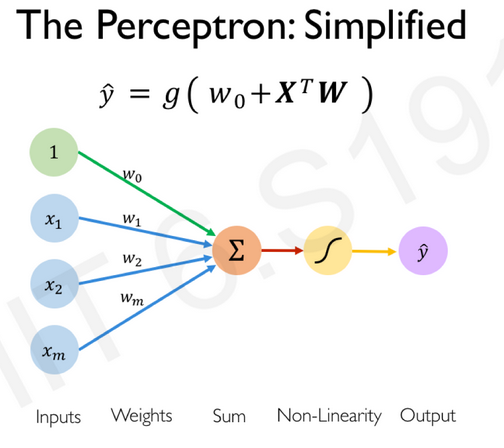
D'après le cours introtodeeplearning du MIT

Une neurone peut s'écrire matriciellement :

$$ z_1 = g(w_0+ X^TW) = g(\begin{pmatrix} 1 & x_{1,1} & x_{1,2} & \cdots & x_{1,p}\\ 1 & x_{2,1} & x_{2,2} & \cdots & x_{2,p}\\ \vdots & \vdots & \vdots & \vdots & \vdots\\ 1 & x_{n,1} & x_{2,2} & \cdots & x_{n,p}\\ \end{pmatrix}\begin{pmatrix} w_0 \\ w_1 \\ \dots \\ w_n \end{pmatrix})$$

Pour un perceptron, la couche cachée $k$ à $i$ neurones, peut s'écrire :

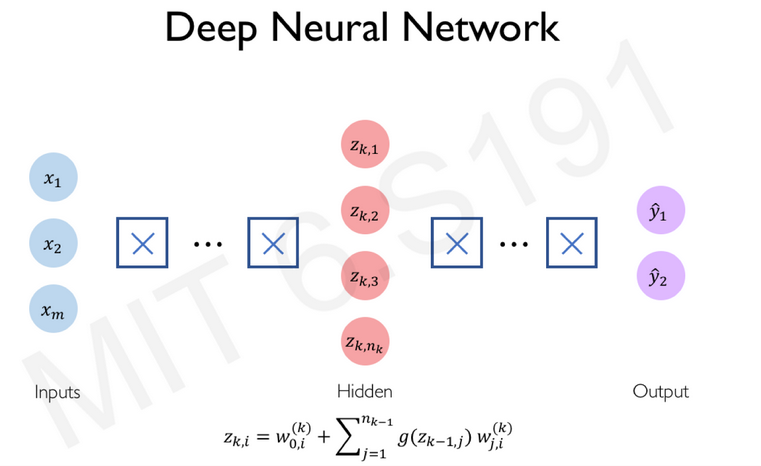
Pour le neurone $i$ de la couche k et le neurones $j$ de la couche k-1 :

$$ z_{k,i} = w_{0,i}^k + \begin{pmatrix} g(z_{k-1,1} & g(z_{k-1,2}) & & \cdots & g(z_{k-1,n_{k-1}})\\ \end{pmatrix} \begin{pmatrix} w_{1,1}^k & w_{1,2}^k & & \cdots & w_{1,i}^k\\ \vdots & \vdots & w_{j,i} & \vdots & \vdots\\ w_{n_{k-1},1} & w_{n_{k-1},2} & & \cdots & w_{n_{k-1},i}\\ \end{pmatrix}$$

Décomposition de matrices

Généralités

La décomposition (ou factorisation) de matrice consiste à diviser une matrice en plusieurs morceaux.

En data data science, on peut l'utiliser par exemple pour sélectionner des parties des données, dans le but de réduire la dimensionnalité sans perdre beaucoup d'informations (comme par exemple dans l'analyse en composantes principales)

Décomposition en vecteurs propres

On peut envisager la décomposition en vecteur propore d'une matrice $A$ comme un changement spécial de base dans laquelle l'espace transformé est une base des vecteurs propres

Vecteurs propres et valeurs propres

Exemple de transformation

Rappelons que l'application d'une transformation représentée par une matrice $A$ sur un vecteur $u$, donne un nouveau vecteur $v$. Par exemple :

$ v = Au = \begin{bmatrix} 1.2 & 0.9 \\0 & -0.4 \end{bmatrix}.\begin{bmatrix} 1.5 \\1 & \end{bmatrix}$

$v = \begin{bmatrix} 2.7\\ -0.4\\ \end{bmatrix}$

On peut représenter le résultat cette transformation:

u = np.array([1.5, 1])
A = np.array([
    [1.2, 0.9],
    [0, -0.4]
])
v = A @ u

Représentation graphique

plt.quiver(0, 0, u[0], u[1], color="#2EBCE7", angles='xy', scale_units='xy', scale=1);
plt.quiver(0, 0, v[0], v[1], color="#00E64E", angles='xy', scale_units='xy', scale=1);

plt.axhline(y=0, c='k');
plt.axvline(x=0, c='k');
plt.xlim(-1,3)
plt.ylim(-1,3)
plt.annotate('u',(1,1),color="#2EBCE7");
plt.annotate('v',(2,-0.6),color="#00E64E");

On peut remarquer que le vecteur $v$ n'est pas colinéaire à $u$ !

Fabriquer un vecteur colinéaire

Que se passerait t'il avec ce vecteur $x$ particulier si on lui applique la matrice $A$ ?

$x = \begin{bmatrix} -0.4902\\ -0.8715\\ \end{bmatrix}$

x = np.array([-0.4902, 0.8715])
y = A @ x
plt.quiver(0, 0, x[0], x[1], color="#2EBCE7", angles='xy',
           scale_units='xy', scale=1)
plt.quiver(0, 0, y[0], y[1], color="#00E64E", angles='xy',
           scale_units='xy', scale=1)

plt.axhline(y=0, c='k');
plt.axvline(x=0, c='k');
plt.xlim(-1,3)
plt.ylim(-1,3)
plt.annotate('x',(-0.5,1),color="#2EBCE7");
plt.annotate('y',(0.25,-0.5),color="#00E64E");

On peut remarquer que le résultats de $Ax$, le vecteur $y$ est colinéaire (ou scaled) par rapport à $x$ !

On appelle $x$ un vecteur propre de la matrice $A$ : il designe un vecteur qui est contracté ou allongé dû à l'application de $A$ La valeur propre est le scalaire qui donne le facteur de ce scaling

Définition

$x$ est un vecteur propre dont les composantes $x_i$ sont associées aux valeurs $\lambda_i$ d'une matrice $A$ si:

$$Ax = \lambda x$$

$$ \begin{bmatrix} A_{1,1} & A_{1,2} & \dots & A_{1,p} \\ A_{2,1} & A_{2,2} & \dots & A_{2,p} \\ \dots & \dots & \dots & \dots \\ A_{n,1} & A_{n,2} & \dots & A_{n,p} \\ \end{bmatrix} \begin{bmatrix} x_1 \\\vdots \\ x_n\\ \end{bmatrix} = \lambda \begin{bmatrix} x_1 \\\vdots \\ x_n\\\end{bmatrix} $$

Interprétation

Intuitivement, on peut l'interpréter comme la transformation qui transforme les vecteurs de l'espace de départ en vecteurs colinéaires (dans l'espace d'arrivée)

On ré-ecrit souvent cette équation de cette manière:

$$(A-\lambda I)x = 0$$

Ou $I$ est la matrice identité

$$ \begin{bmatrix} A_{1,1} - \lambda_i & A_{1,2} & \dots & A_{1,p} \\ A_{2,1} & A_{2,2} - \lambda_i & \dots & A_{2,p} \\ \dots & \dots & \dots & \dots \\ A_{n,1} & A_{n,2} & \dots & A_{n,p} - \lambda_i \\ \end{bmatrix}\begin{bmatrix} x_1 \\\vdots \\ x_n\\ \end{bmatrix} =0 $$

Attention : les vecteurs propres ainsi trouvés ne sont pas uniques !! (on peut multiplier lambda par un scalaire et obtenir des valeurs différentes pour $x_i$)

Reconstruction de la matrice originale

Si on connait les vecteurs propres $x$ et leurs valeurs propres $\lambda$ associées, on peut reconstruire la matrice $A$ originale:

$$ A = x \Lambda x^{-1}$$

ou $\Lambda$ est la matrice transformée

Un des intérêt principaux de la décomposition de matrice consiste à reconstruire la matrice originale en ayant gardé uniquement un certain nombre de paires de valeurs/vecteurs, sans trop perdre d'information

Pour l'explorer plus en détail, voir cette la page interactive de setosa.io

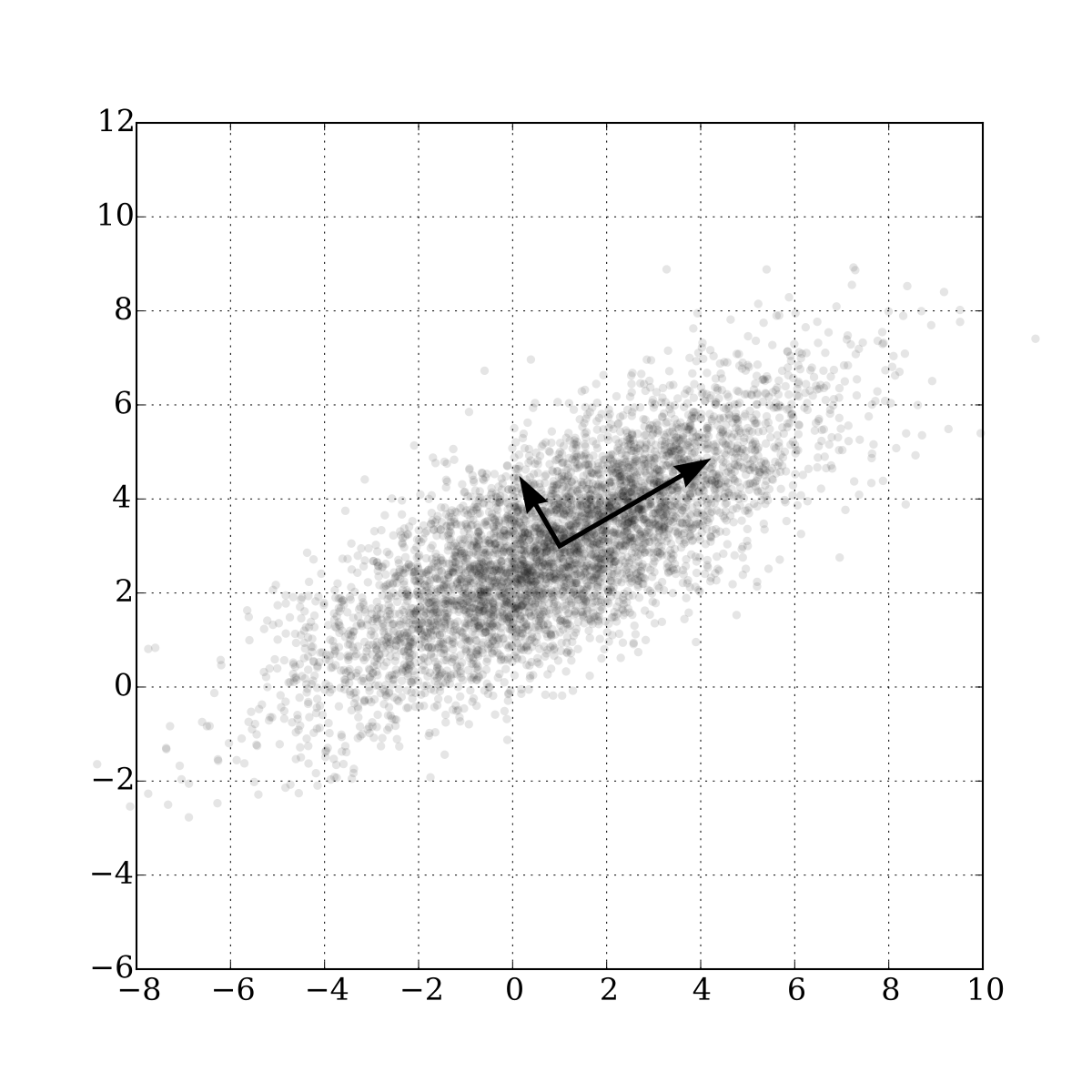
Intuition de l'Analyse en Composantes Principales (ACP)

Principe

Il s'agit d'une méthode de décomposition de matrice en vecteurs propres très populaire, qui est souvent utilisée pour réduire le nombre de variable de votre data set de départ

Elle se calcule en factorisant la matrice de covariance des variables de votre data set

\begin{bmatrix} \sigma_{1,1} & \sigma_{1,2} & \dots & \sigma_{1,p} \\ \sigma_{2,1} & \sigma_{2,2} & \dots & \sigma_{2,p} \\ \dots & \dots & \dots & \dots \\ \sigma_{n,1} & \sigma_{n,2} & \dots & \sigma_{n,p}\\ \end{bmatrix}

Intuition du résultat

Intuitivement, en appliquant la PCA vous calculez un changement de base de votre espace (d'origine) pour former un nouvel espace (d'arrivée) dans lequel les vecteurs de bases sont orthogonaux, maximalement non corrélés, et capturent chacun les directions principales de variance dans votre data set

D'après Nicoguaro

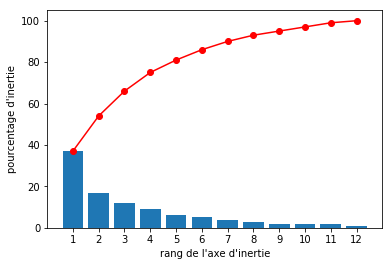
Reduction des composantes

En caclulant une ACP sur vos variables de départ, vous obtenez des paires vecteurs propres (appellées ici composantes) et valeur propres, sélectionnez celle qui expliquent le plus de variance dans votre data set et reconstruisez votres data set de départ en ayant exclus certains de ces vecteurs propres

D'après Open Classroom

Pour aller plus loin

Pour développer une intuition de cet algorithme, allez tester la page interactive de setosa.io

Pour un peu plus de détails, voir cet article d'Hadrien Jean ou le cours dédié d'Open classroom