Lexique des notions importantes

MATHEMATIQUES GENERALES

Notations

Vous rencontrerez parfois certaines grandeurs annotées avec un chapeau (par exemple \(\hat f\)), elle correspondent à la valeur estimé de cette variable lorsque l'on ne connaît pas sa vraie valeur. Par exemple, supposons que l'on cherche à calculer la mesurer la moyenne \(\mu\) de la taille de la population française, mais qu'on ne dispose que d'un échantillon de personne de taille \(N\) pour faire cette mesure, on ne pourra mesurer qu'une estimation \(\hat \mu\) de la vraie valeur de la moyenne \(\mu\) mesurée sur l'ensemble de la population française
La notation arg max lorsque l'on recherche la valeur de la variable qui maximise une expression mathématique donnée.

Notions de bases

Statistiques

En statistique, un biais est un écart entre la vraie valeur d’une variable inobservable et la valeur estimée statistiquement
La variance est une mesure de la dispersion des valeurs d'un échantillon. Elle exprime la moyenne des carrés des écarts à la moyenne. En apprentissage automatique, elle indique également la propension de votre modèle à être sensible aux petites variations entre les données d'apprentissage.

Probabilités

la probabilité conditionnelle :
La probabilité conditionnelle d'un événement A sachant B, notée P(A|B) est la probabilité calculée lorsque l'évènement B est déjà réalisé. Par exemple la probabilité de tirer une carte dans rouge dans un jeu est 1/4, mais elle change si une carte rouge a été tirée (elle vaudra alors 12/56).
la notion de distribution :
Les distributions sont des objets mathématiques qui généralisent la notion de fonction, en ce sens qu'elle étendent la notion de dérivée à des fonctions traditionnellement non dérivables à certains endroits. Ces objets sont souvent utilisés en probabilité, par exemple pour mesurer la densité de probabilité d'une variable. Un exemple de distribution connue est la gaussienne, représentée par une courbe en cloche. Pour plus de détails, vous pouvez allez voir la page wikipédia dédiée, ou regarder cette vidéo

Algébre linéaire

la notion d'espace vectoriel :
C'est un ensemble muni de deux lois de compositions, lois qui permettent de réaliser des opérations sur les éléments de cet ensemble. Les éléments d'un espace vectoriel peuvent être de différentes nature, des nombres, des fonctions, des chats... En ce sens, la notion d'espace vectoriel généralise la notion de vecteur que vous avez vu en géométrie au collège. Pour plus de détails en français, sur les espace vectoriels, je vous invite à consulter ce cours en vidéo. Pour aller plus loin sur la notion de vecteurs, je vous invite fortement à regarder cette excellente vidéo explicative de la chaine 3Blue1brown (anglais) ou cette non moins excellente vidéo (en français) pour des détails concernant leur propriétés.
produit scalaire:
Il correspond à la généralisation du produit que avez utilisé en géométrie avec les vecteurs. Dans un espace vectoriel, il s'agit d'une fonction prenant en entrée deux vecteurs x et y et donnant en sortie un nombre, souvent noté <x, y> Pour plus de précisions mathématiques et d'exemples, je vous invite à regarder cette vidéo (en français)
Matrices: Les matrices sont des objets très utilisés en machine learning, elles correspondent à des tableaux de nombres et forment un espace vectoriel. Je vous invite à regarder cette vidéo de cours (français) pour plus de détails concernant leur propriété.
Les tenseurs: On peut voir les tenseurs comme des tableaux de nombres généralisant la notion de matrices à N-dimensions (par exemple un vecteur est un tenseur d'ordre 1, une matrice un tenseur d'ordre 2, etc ...). Ces objets mathématiques sont en particulier très utilisé dans le deep learning, puisque les équations régissant le fonctionnement des réseaux de neurones s'écrivent souvent avec des tenseurs.
Vecteurs propres et valeurs propres: **
Dans certains problèmes d'algèbres linéaire, on cherche parfois à simplifier une matrice une matrice \(M\) en trouvant une nouvelle base de vecteurs dans laquelle \(M\) s'écrive sous une forme factorisée, c.a.d dans laquelle les éléments diagonaux \(\lambda_i\) sont les valeurs propres de \(M\) et les colonnes de \(M\) ses vecteurs propres**.
Pour ce faire on résout l'équation suivante dans laquelle on cherche les vecteurs propres \(v\) et les valeurs propres \(\lambda = (\lambda_1, \dots \lambda_n)\) tels que: \(Mv=\lambda v\). Pour plus de détails concernant leur calculs je vous invite à regarder cette vidéo

Géométrie

la notion de distance :

En mathématique la distance est une fonction \(d(x,y)\) qui définit la distance entre chaque paire de point d'un ensemble. La distance qui nous est la plus familière est la distance euclidienne, qu'on note souvent :

\(d(x,y) = ||x - y||_2 = \sqrt{(\hat y_1 - y_1)^2 + \ldots +(\hat y_n - y_n)^2}\)

Optimisation

notion d'optimisation:
L'optimisation est une branche des mathématiques cherchant à modéliser, analyser et résoudre analytiquement (par une formule) ou numériquement (par une simulation numérique) les problèmes qui consistent à minimiser ou maximiser une fonction sur un ensemble (source: wikipédia).
En machine learning l'optimisation est utilisée pour minimiser l'erreur entre les prédictions d'un modèle et les labels appris dans le jeu de donnée d'apprentissage. L'objectif général de cette opération est d'apprendre les paramètres du modèle (par exemple les coefficients d'une régression) qui produiront une erreur minimale. Pour plus de détails, je vous invite à suivre ce cours en anglais.
méthode des moindre carré:
il s'agit d'une méthode d'optimisation, très souvent utilisée dans les tâches de régression et permet de résoudre de manière exacte (dans le cas de la régression linéaire) le problème de minimisation de la fonction de loss.
descente du gradient:
Le gradient correspond à la généralisation de la notion de dérivée, lorsqu'il s'agit de fonction de plusieurs variables (f(x,y,...)). Tout comme la dérivée il peut être interprété comme la pente de la tangente au graphe de la fonction étudiée. Plus précisément, le gradient est une fonction vectorielle (par opposition à la dérivée qui est une fonction scalaire), c'est à dire qu'elle correspond à vecteur (un élément d'un espace vectoriel).
La notion de gradient est importante et sert dans l'algorithme de descente du gradient, qui est très souvent utilisé en machine learning pour minimiser, par exemple, l'erreur entre les prédictions et les labels appris.
Pour plus de détails vous pouvez consultez les pages wikipedia pour le gradient et l'algorithme de la descente du gradient et regarder ce tutoriel vidéo en français. Pour vous faire une compréhension empirique de ce dernier, je vous invite à regarder ce tutoriel proposant du code python calculant et représentant la descente du gradient avec des fonctions de plusieurs variables.

DATA SCIENCE

ALGORITHMIE

Complexité algorithmique

Intuitivement, il s’agit de mesurer le nombre d’opérations élémentaires effectuée par un algorithme.

Plus précisément, la complexité algorithmique vise à évaluer (à des fins de comparaison) le temps et la mémoire nécessaire dont un algorithme à besoin pour fonctionner. La complexité permet de quantifier (via une formule mathématique) la relation entre les conditions de départ définies par le problème et le temps effectué par l'algorithme. Une des approches pour faire cette analyse consiste à faire le benchmark de différents algorithmes, mais cette méthode est souvent spécifique d’un langage, de la configuration d’un ordinateur, de la qualité de l'implémentation, des données d’entrées ...

Une seconde approche plus populaire consisté à faire l’analyse mathématique des algorithmes, qui est indépendante de leur implémentation et des entrées.

En pratique donc, cette notion permet de mesurer de l'efficacité algorithme en terme de temps de calcul, en considérant un ordinateur idéalisé avec une mémoire infinie.

Analyse asymptotique

Il s'agit de la mesure du comportement de l’algorithme quand l’entrée de l’algorithme tend vers l’infini (n \(\rightarrow \infty)\). Par exemple si votre algorithme prend en entrée une liste, l’analyse asymptotique s’intéresse à la complexité de l’algorithme quand le nombre d’item de la liste est très grand. Par conséquence, cette analyse ne prend pas en compte les temps qui sont constants (comme par exemple le temps pour faire appel à un autre algorithme) et les facteurs multiplicatifs constants de l’entrée (on ne fait pas la différence entre un algorithme qui calcule en N ou en 7N opérations). La complexité asymptotique se note en général avec le symbole \(O()\) ou notation de Laudau. En résumé cette mesure de la complexité ne prend en compte qu’ un ordre de grandeur du nombre d’opérations effectué par un algorithme qui est pratique pour grouper les algorithmes ayant des temps d’exécution à l’infini

Notation O()

La notation \(O()\) réfère à l’analyse asymptotique dans laquelle on évalue une estimation du nombre d’étape nécessaires à un algorithme lorsque n tends vers l’infini. Pratiquement, on est souvent incapable de donner une formule précise à cette fonction, mais on cherche à estimer sa forme canonique, et ce afin de comparer différentes classes d’algorithmes.

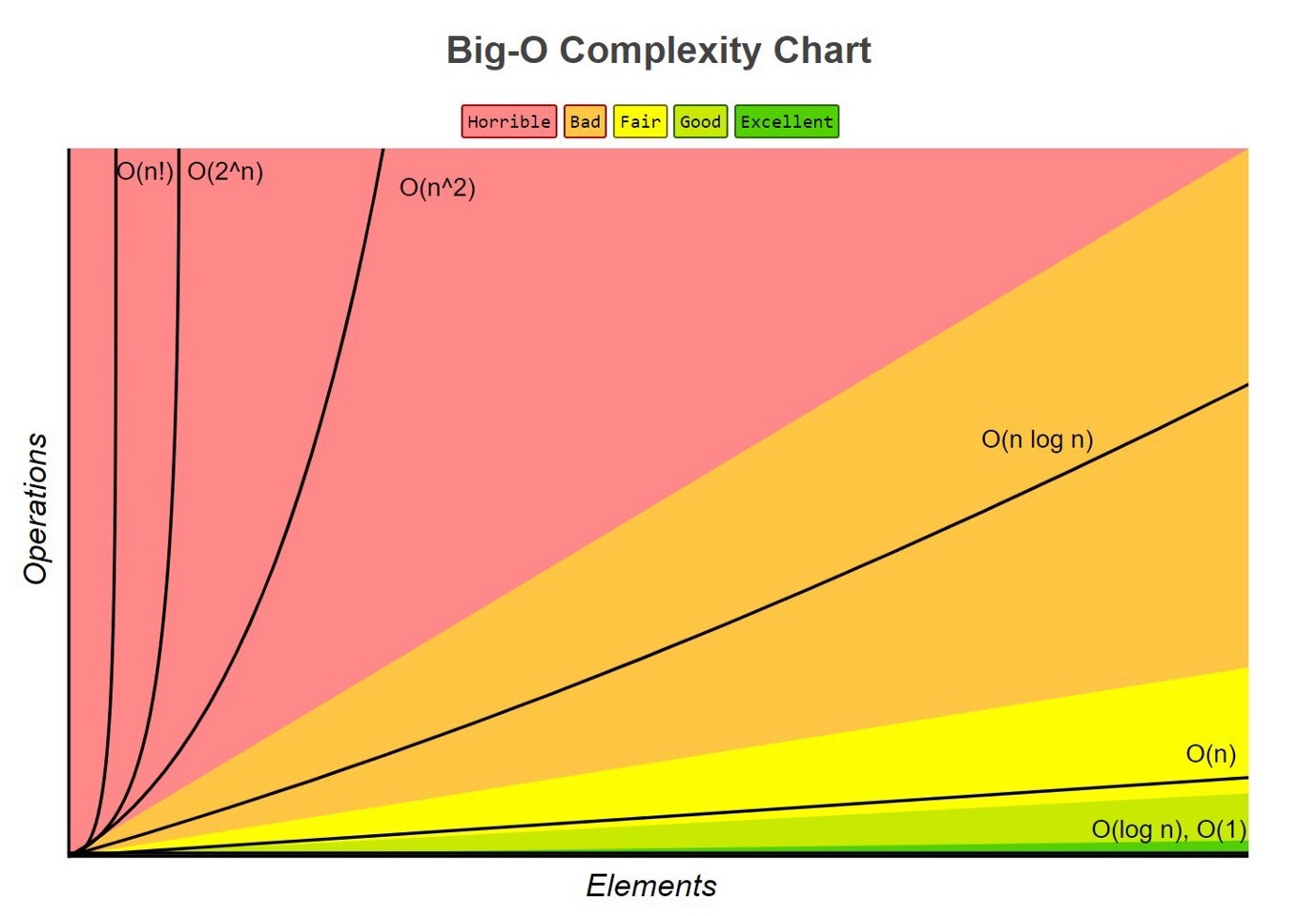
Voici quelques cas courants:

\(O(log(n))\) caractérise les algorithmes qui opèrent en un temps logarithmique (la plus faible)
\(O(n)\) caractérise les algorithmes qui opèrent en un temps linéaire
\(O(n^k)\) caractérise les algorithmes qui opèrent en un temps polynomial
\(O(a^n)\) caractérise les algorithmes qui opèrent en un temps exponentiel (la plus forte)

Complexité algorithmique et classes de problèmes

La théorie de la complexité informatique, est le domaine des mathématiques, et plus précisément de l'informatique théorique, qui étudie formellement la quantité de ressources (temps, espace mémoire, etc.) dont a besoin un algorithme pour résoudre un problème algorithmique. Il s'agit donc d'étudier la difficulté intrinsèque de problèmes, de les organiser par classes de complexité et d'étudier les relations entre les classes de complexité.

La première classe de problème dits ‘faciles’ à résoudre sont les problèmes appelés P pouvant être résolu par un algorithme dans un temps polynomial. Cette classe contient par exemple les problèmes de type \(O(n)\) et \(O(log(n))\)
La classe NP, signifiant non deterministic polynomial problem, contient les problèmes pour lesquels un algorithme peut être trouvé pour proposer une solution et si ensuite cet algorithme est exécutable dans un temps polynomial. La question de savoir si cette classe est équivalente à la classe P (le problème P=NP) est un problème ouvert en informatique.

Pour plus de détails sur la complexité algorithmique

lire cet excellent article du blog towards data science
lire ce chapitre de cours d'Open Classroom

PROGRAMMATION

Python

Concernant les fonctions et classes

args : Il s'agit d'une dénomination courante pour les arguments optionnels (stockés dans une liste) que vous pouvez passez à une fonction ou une classe. Lorsque l'on ne connait pas à l'avance le nombre de paramètre d'une fonction, il est possible de passer des arguments optionnels à une fonction (sous la forme d'une liste), avec la syntaxe suivante:

fonction(argument1, argument2, *args)

kwargs ou keywords arguments: Il s'agit d'une dénomination courante pour les arguments par défaut que vous pouvez passez à une fonction ou une classe. Lorsque l'on ne connait pas à l'avance le nombre de paramètre d'une fonction, il est possible de passer des keywords arguments optionnels à une fonction (sous la forme d'un dictionnaire) avec la syntaxe suivante:

fonction(argument1, argument2, **kwargs)

MACHINE LEARNING

Notions générales

Apprentissage supervisé

En apprentissage automatique, une tâche de classification consiste à prédire, pour une nouvelle donnée, la classe à laquelle elle appartient. La classe (ou label) correspond à des catégories discrètes (par exemple, 'chat', 'chien', ou 0,1, ...). Lorsque la tâche consiste à prédire plusieurs catégories simultanément, on dit qu'elle est multi-classe (par exemple lorsque l'on doit prédire le label 'fruit' parmi une catégorie d'objets et le label 'ananas' pour catégoriser chaque fruit)
Lorsque les labels à prédire sont des données continues (par exemple des valeurs de température) on parle de tâche de régression.
clusters: dans l'apprentissage non supervisé, désigne les groupes ou partitions que l'on veut identifier dans les données.
centroides: dans les algorithmes de clustering (tels que K-means), désigne les centres des clusters que l'on veut identifier.

Notions mathématiques importantes

Glossaire de Google

Le glossaire de google pour les développeurs reprend de manière très synthétisée un bon nombre de notions liées au machine learning (et en particulier au deep learning) et son implémentation.

Statistiques appliquée au machine learning

courbe ROC (Receiver Operating Characteristic) :
La courbe ROC est une métrique souvent utilisée en machine learning pour évaluer la performance d'un classifieur binaire. En particulier, le calcul de l'aire sous la courbe ROC, indice qui varie entre 0 et 1, fournit un indice de la performance de classification. Pour plus de précisions et d'exemples, voir la page wikipédia dédiée.
Variable latente:
En statistique, une variable latente (du latin lateo signifiant caché) sont des variables qui ne sont pas directement observables mais plutôt inférées par un modèle mathématique à partir des variables observées.
Par exemple, l'Analyse en Composante Principale (ACP) est capable de combiner de manière linéaire les variables d'entrées pour "fabriquer" de nouvelles variables qui sont des variables latentes (ont les nomme souvent composantes dans le cas des méthodes comme l'ACP)
notion de validée croisée ou cross validation:
La validation croisée sert à tester la capacité d'un modèle à généraliser ses performances sur des données qu'il n'a jamais rencontrées, en évitant le sur apprentissage. La validation croisée est surtout utilisée dans un contexte ou la taille du jeu de donnée n'est pas suffisante pour le découper en trois parties (classiquement, le jeu d'apprentissage, le jeu de validation et le jeu de test). Dans la validation croisée, on "s'économise" la constitution du jeu de validation, en tirant un grand nombre de fois (souvent au hasard) un échantillon qu'on utilise pour tester la capacité de généralisation de notre modèle, puis qu'on remet dans le jeu d'apprentissage pour la prochaine itération. je vous invite à voir cette vidéo de vulgarisation pour plus d'exemples.
le grid search:
La méthode du grid search est une méthode populaire de sélection des hyper-paramètres d'un modèle. Elle consiste à définir un ensemble de valeurs des hyper-paramètres que l'on veut tester, afin d'en choisir les valeurs optimales. Cet ensemble de valeurs peut se représenter sous la forme d'une grille dans laquelle chaque point correspond à une combinaison particulière des hyper-paramètres à tester. Dans la pratique, cet algorithme teste automatiquement toutes les valeurs possibles de la grille et permet de sélectionner les hyper-paramètres optimaux.
notion de régularisation Dans le domaine de l'apprentissage automatique, la régularisation fait référence à un processus consistant à ajouter de l'information à un problème pour éviter le sur-apprentissage. Cette information prend généralement la forme d'une pénalité envers la complexité du modèle. Une méthode généralement utilisée est de pénaliser les valeurs extrêmes des paramètres, qui correspondent souvent à un sur-apprentissage. Pour cela, on va utiliser une norme sur ces paramètres, que l'on va ajouter à la fonction qu'on cherche à minimiser.

Algèbre non linéaire et topologie

La notion de plongement (embedding):
En mathématiques, un plongement intervient lorsqu'une instance d'une structure mathématique X est contenue dans une autre structure Y, généralement de dimension plus grande. Plus précisément, le plongement se caractérise par une fonction injective f permettant de lier n'importe quel point de l'espace de départ X à l'espace d'arrivée Z en préservant la structure de X.
Par exemple, il existe une fonction injective permettant de transformer l'ensemble de nombres naturels, en celui des entiers, celui des entiers en celui des nombres rationnel, ... tout en préservant leur caractéristiques.
Intuitivement, en machine learning, on utilise les plongements comme n'importe quelle transformation, pouvant se modéliser par une fonction injective, pour trouver un nouvel espace de représentation des données dans lequel celles-ci sont plus facilement traitables par les algorithmes de machine learning (par exemple pour faire une meilleure classification). D'après la page wikipédia dédiée
La notion de variété (manifold):
En mathématiques, une variété est un espace topologique qui ressemble localement à un espace euclidien. Plus précisément, une variété de dimension \(n\), est un espace dans lequel chaque point possède un voisinage qui est homéomorphe à un espace euclidien. Basiquement, on peut voir une variété comme un espace ayant localement (au voisinage de chaque point) point les mêmes propriétés qu'un espace euclidien.
Par exemple, les lignes et les cercles sont de variétés de dimension 1 mais pas la figure 8 (car il n'existe pas de voisinage du point de croisement étant homéomorphe à un espace euclidien). Le plan, la sphère et le tore sont des variétés de dimension 2.
Pratiquement, en machine learning, l'apprentissage de variété peut se concevoir comme une forme de généralisation des méthodes linéaires de plongement, de sorte qu'elle permettent de définir un nouvel espace pour représenter les données, espace dans lequel les non-linéarités dans les données sont globalement préservées.
D'après la page wikipédia et celle de scikit-learn dédiées