Résolution de problemes appliquée au jeux

Comment définir un problème ?

La résolution de problème fait partie historiquement d'un des grand domaines de l'Intelligence Artificielle. Dans ce domaine, de nombreux problèmes qui se rapportent à un environnement déterministe, observable, statique et complétement connu, peuvent être résolu par des agents capables de trouver des solutions à ces problèmes en construisant des sequences d'actions répondant à un but (les goal-based agents).

Mathématiquement, ces problèmes se caractérisent par six propriétés:
- une représentation de l'environnement par un espace des états - un état initial s avec lequel l'agent démarre.
- une description de toutes les actions possibles par l'agent qui se modélise par une fonction $Actions(s) ⟶ {a_1,a_2, a_3, ...}$
- une description des résultats de chacune de ces actions qui se modélise par une fonction qui renvoie un nouvel état s', résultat de l'action a effectuée dans l'état s: $Resultats(s, a) ⟶ s'$
- une fonction de but interne à l'agent qui lui permet de décider si l'état en cours s correspond à un état à atteindre.
- une solution au problème, définie comme un chemin à travers l'espace des états entre l'état initial et le but.
- une fonction de cout qui détemine une valeur numérique pour chaque chemin dans l'environnement.

Les algorithmes de recherche de graphe sont une classe de solutions très populaire pour ce genre de problème; certains de ces algorithmes ont permis de réaliser des progrès important dans la recherche en Intelligence Artificielle depuis ses débuts à nos jours, notamment dans les jeux.

Les jeux en tant que problèmes

Dans l'Intelligence Artificielle, les jeux intéressent beaucoup les chercheurs car ils appartiennent à une catégorie de problèmes difficile à résoudre, contrairement à des problèmes plus simple pour lequel on connait des algorithmes offrant une solution optimale, comme par exemple, le problème du plus court chemin.

Ainsi les problèmes associés au jeux possèdent des contraintes additionnelles du fait de la présence d'un ou plusieurs adversaires:
- les solutions et leur optimalité dépendent des caractéristiques des adversaires.
- les agents doivent souvent trouver des réponses dans un temps limité, ce qui exige parfois la recherche de solution approximative.
- la création d'une bonne fonction d'évaluation des états de l'environnement (ou ici, les situations de jeu) est délicate et dépend fortement des propriétés du jeu.

Caractérisation de notre environnement de tâche pour le projet Pac Man

Dans notre projet Pac Man multi agent, il est impératif de définir notre environnement de tâche afin de pouvoir modéliser notre problème et d'en chercher des solutions. L'environnement de tâche du jeu est:

totalement obervable: Pac Man connaît la totalité de l'environnement du jeu (voir dans le code l'objet GameState).
multi-agent: vous devrez modéliser le comportement de Pac Man en prenant en compte celui des fantômes.
adverse: les fantômes cherchent à éliminer Pac Man.
déterministe: les actions de Pac Man ne sont influencées par aucune variable aléatoire.
séquentiel: vous avez plutôt intérêt à considérer que l'état du jeu à un instant t-1 puisse influencer les actions de Pac Man à l'état à l'instant t.
discret: les actions possibles de Pac Man sont dénombrables.
connu: vous avez plutôt intérêt à donner à Pac Man la connaissance à priori des règles qui régissent son environnement.

Parcours de graphes & arbres : le contexte des jeux

Si vous n'êtes pas familier avec la notion de graphes, vous en avez sûrement déja utilisé sans le savoir. Par exemple, si vous avez déja utilisé un GPS pour vous rendre d'un point A à un point B, vous avez expérimenté une classe d'algorithmes dédiée à résoudre le problème du plus court chemin, algorithmes qui fonctionnent en visitant un graphe représentant la carte de votre voyage.

De la même manière que le problème du plus court chemin peut se modéliser sous forme de graphe et en particulier sous forme d'arbre (une sous catégorie de graphe), la plupart des jeux se prêtent bien à cette modélisation. Dans ce type de modélisation, qu'on appelle alors d'arbre de jeu, les noeuds représentent des état de l'environnement (ici des situations de jeu) et les arrêtes les mouvements possibles des joueurs.

Dans certains jeux simples comme le tic-tac-toe (qui ne possède que 362 880 noeuds terminaux), l'arbre de jeu peut modéliser complètement l'ensemble des états possibles jusqu'aux états terminaux qui représentent les états de fin de partie et dont la valeur est évaluée par la fonction d'utilité.

Exemple d'un arbre de jeu pour le tic-tac-toe
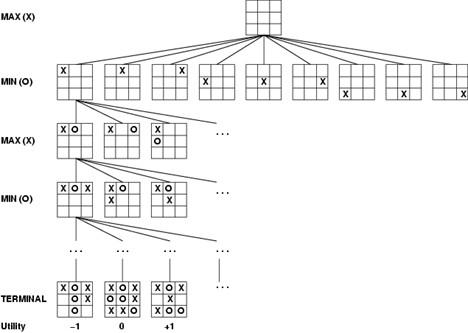
Figure 3.1: Exemple d'arbre (partiel) de jeu pour le tic-tac-toe. Le noeud racine correspond à l'état initial de la partie, puis les coups du joueur MAX sont représentés pas les X et ceux du joueurs MIN par les O. Les noeuds terminaux représentent les états finaux possible de la partie, qui sont évalués par une fonction d'utilité.

Cependant la plupart des jeux sont trop complexes pour qu'on puisse les représenter complétement par un arbre, c'est le cas par exemple des échecs dont l'arbre de jeu serait constitué de $10^{40}$ noeuds ! Dans ce genre de cas, on utilise alors des arbres de recherche qui représentent uniquement un nombre suffisant d'états pour permettre à notre agent de choisir le coup à jouer. Suivant cette modélisation, on peut utiliser des méthodes de parcours de graphe pour trouver la solution au problème du jeu, à savoir déterminer le meilleur coup à jouer.

Dans le cas de notre projet Pac Man , le choix des actions de Pac Man peuvent se modéliser par un arbre de recherche, c'est le premier ingrédient pour notre agent rationnel.

Fonction d'utilité et fonction d'évaluation

Le second ingrédient pour modéliser le comportement d'un agent rationnel comme notre Pac Man consiste à pouvoir évaluer l'utilité des situations de jeu à chaque instant. Le concept de fonction d'utilité vient des domaines de la théorie de la décision et de l'économie. Transposée au domaine de l'Intelligence Artificielle, la fonction d'utilité sert à estimer une valeur pour les états terminaux d'un environnement, par exemple, dans le cas d'un jeu, en assignant la valeur +1 pour le gain et la valeur -1 pour une perte de la partie. Cette fonction permet aux agents de décider de leurs actions en cherchant à maximiser leur fonction d'utilité, il s'agit des utility-based agents vus au chapitre sur les agents intelligents.

Dans un jeu simple pour lequel on pourrait modéliser et calculer toutes les situations de jeu dans un temps acceptable, la fonction d'utilité seule pourrait suffire à déduire, en partant des états terminaux, les valeurs des situations de jeu intermédiaires, mais ce cas est très rare dans la pratique. Dans la plupart des jeux, nous aurons besoin d'estimer la valeur des situations de jeu intermédiaires, en évaluant la possibilité que ces situations puissent conduire à la victoire d'un joueur donné. On utilise pour ce faire une fonction d'évaluation qui est souvent difficile à modéliser. La modélisation de cette fonction nécessite souvent des connaissances sur le jeu et n'est pas souvent garantie d'être optimale, c'est pourquoi on ne se contente souvent d'utiliser une heuristique de fonction d'évaluation.

Par exemple, aux échecs on attribue des valeurs à chaque pièce en fonction de sa puissance. Une heuristique de fonction d'évaluation souvent utilisée consiste à calculer la différence de la valeur des pièces capturées par chacun des joueurs.

Algorithme minimax

Définition et première intuition

L'algorithme minimax est un algorithme récursif de parcours de graphe utilisé dans les jeux à n joueurs pour choisir les actions que doit effectuer un joueur (ou un agent artificiel). Il permet de calculer la valeur pour chaque état s de l'environnement à partir d'une heurisitique de fonction d'évaluation qui permet d'approximer l'utilité de l'état s (savoir s'il s'agit d'une bonne ou mauvais actions à jouer). Cet algorithme est souvent utilisé en particulier dans les jeux à somme nulle, un sous domaine de la théorie des jeux. Dans ce type de jeux, correspondant à environnement de tâche adverse, la problématique réside dans le fait que chaque joueur va chercher à maximiser la valeur état s de l'environnement . Dans un jeu de plateau comme les échecs par exemple, il faut prendre en compte dans le choix des coups le fait que l'adversaire cherche également à maximiser son coup, il est alors simpliste de se contenter de simplement choisir le "meilleur coup dans l'absolu".

Intuitivement, l'algorithme minimax répond à ce problème en proposant une règle de décision qui vise à minimiser la possible perte maximale (correspondant au pire des scenarii possible pour notre agent). Il calcule la valeur minimax pour notre agent, c'est à dire la valeur minimale de l'état s que les autres joueurs peuvent engendrer, sans connaître leur actions.

Description

Dans cette description nous supposerons, pour simplifier, que deux joueurs sont adversaires, le joueur A (qui correspond à l'agent que l'on souhaite modéliser) et son adversaire, le joueur B. Notez bien que ce joueur fonctionne avec n joueurs/agents, ce qui correspond à votre cas pour la modélisation de vos agents dans le projet Pac Man (Pac Man & les fantômes). Généralement, lorsque l'on décrit cet algorithme, on désigne le joueur A comme le joueur maximisant et son adversaire, le joueur B, comme le joueur minimisant.

Dans la plupart des jeux, il est souvent irréaliste de pouvoir modéliser tous les états du jeu jusqu'aux états terminaux car le temps d'éxecution de l'algorithme minimax serait trop important. Dans la pratique, on souhaite appliquer minimax sur un arbre suffisamment profond pour que sa performance soit importante, tout en conservant un temps d'éxecution acceptable. Cet arbre est d'autant plus profond que l'on modélise de futurs tours de jeu par joueurs, les plies. La figure 3.2 ci-dessous représente un exemple d'arbre de recherche simpliste dans lequel sont représentés uniquement 3 états du jeu.

Exemple d'un arbre de jeu simpliste
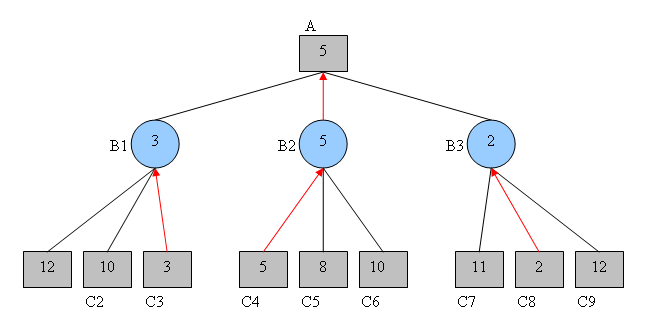
Figure 3.2: Exemple simpliste d'un arbre représentant trois tours de jeu dans un jeu à somme nulle avec deux joueurs. Chaque noeud représente la valeur estimée de la situation de jeu pour notre agent, le joueur A (rectangles gris) et son adversaire, le joueur B (ronds bleu).

Voyons maintenant les étapes du processus de fonctionnement de l'algorithme Minimax. Celui-ci fonctionne de manière récursive et ascendante:

\[ Minimax(s) = \left\{ \begin{array}{ll} utilité(s) & si~noeud = noeud~terminal \\ max_{a\in Actions(s)}~Minimax(Result(s,a)) & si~Joueur(s) = MAX\\ min_{a\in Actions(s)}~Minimax(Result(s,a)) & si~Joueur(s) = MIN\\ \end{array} \right. \]

On part des noeuds terminaux de l'arbre auquel on attribue une valeur d'utilité par une heuristique de fonction d'évaluation. Ensuite, on remonte l'arbre et on évalue les noeuds précédents successivement jusqu'au noeud racine (qui correspond à l'état actuel du jeu).
Si les noeuds correspondent à ceux de l'adversaire, c'est à dire le joueur minimisant (ronds bleus), on calcule leur valeurs pour chacun d'eux en minimisant le minimax de chacun des ses noeuds fils. Intuitivement, on cherche à sélectionner le minimum de la pire situation de jeu que pourrait jouer notre agent (joueur A) en réponse au coup du joueur B.
Si les noeuds correspondent à ceux de notre agent, c'est à dire le joueur maximisant (rectangle gris), on calcule leur valeurs pour chacun d'eux en maximisant le minimax de chacun des ses noeuds fils. Intuitivement, on cherche à sélectionner le maximum de la pire situation de jeu que pourrait provoquer l'adversaire (joueur B) en réponse au coup de notre agent.

L'algorithme s'arrête lorsque l'on est remonté jusqu'au noeud racine qui est évalué par l'heuristique de la fonction d'évaluation. En général, la qualité de l'estimation de la valeur des noeuds terminaux et la profondeur de l'arbre détermine la qualité du résultat final (le prochain mouvement à jouer).

Pour plus de détails interactifs concernant le fonctionnement de Minimax, vous pouvez visionner cette bonne vidéo.

Limitations de minimax & améliorations possibles

Dans la plupart des jeux, le nombre de situations de jeu possible est très grand, comme c'est le cas par exemple au échecs et encore plus au go. De plus, le parcours de l'abre par l'algorithme minimax, le nombre de noeuds à explorer augmente exponentiellement avec le nombre de tours de jeu (plies), ce qui tend à rendre l'algorithme incalculable dans un temps acceptable. C'est pourquoi dans la pratique, on limite très souvent la profondeur de l'arbre à une dizaine de tours de jeu. A titre d'exemple, le minimax utilisé par Deep Blue dans sa victoire contre Kasparov au échec avait une profondeur de 12 tours de jeu.

En général, une des manières les plus répandues de réduire temps de calcul d'algorithme de parcours d'arbres consiste à "élager", certaines branches de l'arbre qui ne seront ainsi pas visitées. En particulier dans le cas de l'algorithme minimax, il existe un algorithme d'élagage, l'algorithme d'élagage alpha-beta qui donne les mêmes résultats que l'algorithme minimax "naif" mais sans visiter certaines branches qui n'influenceraient pas la décision finale.

Elagage alpha-beta

Principe général

Tout comme minimax, il s'agit d'un algorithme de parcours de graphe en profondeur : à chaque noeud, il n'explore d'abord que les noeuds fils. Appliqué a minimax, il permet ainsi de parcourir le graphe en profondeur tout en élagant certaines branches à ne pas visiter en fonction de deux valeurs α et β. Il à l'avantage de donner les même résultats qu'aurait donné minimax seul, mais avec un temps d'éxecution moindre.

Tout au long du parcours du graphe, l'algorithme calcule les valeurs α et β définies comme suivant:
- α = plus grande valeur que l'on peut garantir jusqu'ici (dans la branche en cours de visite) pour le joueur maximisant
- β = plus petite valeur que l'on peut garantir jusqu'ici (dans la branche en cours de visite) pour le joueur minimisant

L'algorithme s'éxécute comme suit :
1. Initialisation des valeurs telles qu'elle correspondent au pire score possible pour chaque joueur (α = -∞ et β = +∞)
2. on met à jour les valeurs α et β au fur et à mesure de la visite de l'arbre et on élimine les nœuds (et leur branches associées) ayant des valeurs v telles que α ⩾ v et β ⩽ v.

Exemple d'un arbre alpha-beta
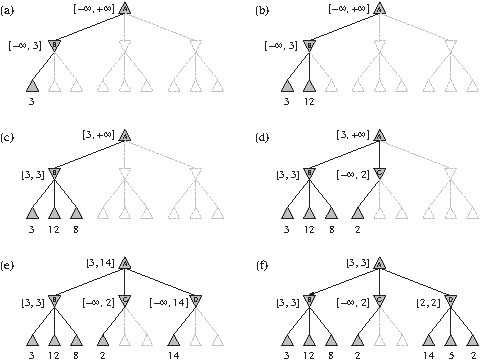
Figure 3.3: Exemple d'application de l'élagage alpha-beta.

Jeux stochastiques

Jusqu'a présent nous avons évoqué uniquement des jeux purement déterministes, dans lesquels aucun élément de l'environnement de tâche n'est dépendant du hasard. Dans beaucoup de situations de la vie réelle certains événements sont imprédictibles. Certains jeux imitent ce caractère imprédicitble, en incluant pas exemple des élements aléatoires comme des lancés de dés, on parle alors de jeux stochastiques. Dans ce type de jeux, les décisions de notre agent vont donc reposer sur des phénomènes aléatoires qu'il faut modéliser.

Le backgammon est un bon exemple de jeu en partie stochastique puisqu'il nécessite de combiner des talents de prise de décision et une partie de chance. Le but du jeu pour chaque joueur consiste à déplacer des pions sur un plateau et de réussir à tous les sortir du plateau. L'élément aléatoire provient du fait qu'à chaque tour chaque joueur lance des dés qui indiqueront les coups possibles à effectuer pour ce joueur et ce tour. Ainsi lorsque le 1er joueur commence à jouer, il ne connait pas encore les coups légaux pour son adversaire, qui seront déterminés par un lancé de dé. Cette contrainte pose un problème de modélisation des situations de jeu, car nous ne pouvons plus utiliser ici un arbre de jeu simple comme nous l'avons vu précédemment pour le tic-tac-toe ou les échecs.

Expectiminimax

Cet algorithme est une variation de l'algorithme minimax deont principe général consiste à étendre l'arbre utilisé dans l'algorithme minimax en y ajoutant un nouveau type de noeuds, les noeuds chance qui vont servir à modéliser les élements aléatoires du jeu. On construit alors un nouveau type d'arbre en alternant des noeuds de type min, max et chance.

L'algorithme fonctionne de manière similaire à celui de minimax pour le calcul des valeurs des noeuds terminaux et des noeuds min et max. Par contre, pour estimer la valeur de chaque noeud chance on calcule sa valeur attendue qui correspond à la somme des valeurs de ses noeuds fils du phénomène, pondéré par leur probabilité d'apparition. Mathématiquement, on calcule donc la valeur du noeud chance n par la formule: $expectiminimax_n = \sum_{c \in C} P_c V_c$

Avec C l'ensemble des noeuds fils c du noeud courant n, $P_c$, la probabilité d'occurence de l'évenement représenté par le noeud c, $V_c$ la valeur courante du noeud c (résultat de l'application récursive de la fonction expectiminimax sur les noeuds fils de c) Le pseudo-code de l'algorithme est donnée dans la partie Annexes

Pour reprendre l'exemple du backgammon, les joueurs lancent deux dés pour déterminer les coups légaux. Au noeud chance n, la somme des valeur $V_c$ est pondérée par les probabilités d'occurence des dés: $\frac{1}{36}$ pour les faces identiques et $\frac{1}{18}$ pour les autres combinaisons.

Exemple d'un arbre expectiminimax
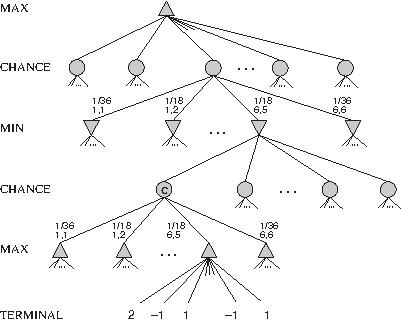
Figure 3.4: Exemple d'application de l'algorithme expectiminimax.

Application aux jeux multi joueurs

Attention, dans les exemples présentés ci-dessus, nous avons représenté, par souci de simplicité, des jeux à somme nulle à deux joueurs. Les algorithmes de parcours de graphes que nous avons évoqué plus haut s'appliquent également dans un contexte de jeux multi joueur. C'est dailleurs le cas dans l'environnement de tâche de notre jeu Pac Man: il va falloir que vous modélisiez les actions des plusieurs ennemis sur l'état du jeu. Un piste pour adapter les exemples vus plus haut va consister à ajouter dans vos algorithmes de recherche de graphe d'autres joueurs, les fantômes. De plus vous devrez adapter la fonction d'évaluation pour qu'elle renvoie, à chaque noeud un n-uplet (tuple) de valeurs plutôt qu'une valeur unique.

Exemple d'un minimax multi-joueur
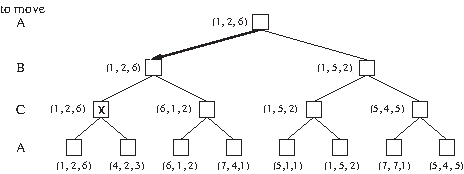
Figure 3.5: Exemple d'application de l'algorithme minimax avec 3 joueurs A, B et C.

Quelques pistes de recherches pour votre projet

Faire varier le nombre de tour de jeux (plies) à prendre en compte dans votre arbre.
Faire varier la fonction d'évaluation utliser.
Tester les variantes de l'algorithme minimax: l'élagage alpha-beta et expectiminimax
Utiliser des heuristiques particulières pour modéliser des buts.

Par exemple, il pourraît être intéressant de tester une stratégie audacieuse dans laquelle Pac Man chercherait à s'orienter vers les boules lui permettant de manger les fantômes (ce qui accorde plus de points) en utilisant des algorithmes de recherche du plus court chemin, ou au contraire stratégie prudente dans laquelle Pac Man chercherait à rester le plus loin possible des fantômes, ce qui pourrait être utile dans les cas ou les fantômes sont lancé en mode aggressif.
Aller explorer d'autres algorithmes plus sophistiqués comme Iterative deepening, SSS*, Max$^n$ search, Monte carlo tree search

Lexique du chapitre

Vocabulaire de la théorie des graphes

Un graphe est un objet mathématique de la théorie des graphes composé de noeuds, représentant une valeur et de relations entre eux, les arêtes.
Un arbre est un cas particulier de graphe non orienté, acyclique et connexe. Il possède des nœuds particuliers qu’on appelle racine (le nœud qui n’a pas de parents) et feuilles (nœuds qui n’ont aucun enfant).
Un graphe orienté est un graphe dans lequel les noeuds sont associé suivant une direction indiquant le sens de parcours du graphe, représentée par une flèche.
Contrairement au graphe orienté, le graphe non orienté ne possède pas de direction définissant son sens de parcours.
Un un graphe non orienté G = (S,A) est dit connexe si, quels que soient les sommets u et v de S, il existe une chaîne reliant u à v
Une branche est ensemble fini de noeuds et d'arrêtes (connexes) constituant un sous-graphe.
Un arbre enraciné est un graphe acyclique orienté possédant une racine unique et dans lequel tous les noeuds sauf la racine possèdent un unique parent.
Un algorithme de parcours de graphe est un type d'algorithme consistant à visiter les noeuds d'un graphe. Il existe plusieurs stratégies différentes de parcours de graphe comme le parcours en profondeur ou le parcours en largeur.

Vocabulaire de la théorie des jeux

Un jeu à somme nulle est un jeu dans lequel la somme des gains et des pertes de tous les joueurs est égale à 0. Cela signifie donc que le gain de l'un constitue obligatoirement une perte pour l'autre. Par exemple si l'on définit le gain d'une partie d'échecs comme 1 si on gagne, 0 si la partie est nulle et -1 si on perd, le jeu d'échecs est un jeu à somme nulle.
Dans un jeu séquentiel à 2 joueur, un ply est un tour joué par un des deux joueurs.

Vocabulaire de l'informatique et de l'algorithmie

Dans le domaine de la résolution de problème, une heuristique correspond à une solution pratique à un problème, qui n'est pas garantie d'être optimale ou rationnelle mais qui est suffisante pour atteindre rapidement un objectif à court terme. Lorsque l'on ne connaît pas de solution optimale à un problème ou que celle-ci est incalculable, alors les méthodes heuristiques servent souvent améliorer le temps de calcul pour une solution satisfaisante.

Par exemple, A*, un algorithme utilisé dans le problème de la recherche du plus court chemin utilise une heuristique souvent choisie comme la distance à vol d'oiseau entre la point de départ et la destination. Grâce à l'usage de cette heuristique il est plus rapide que son concurrent qui offre une solution optimale, l'algorithme de Dijkstra.
Un arbre de recherche (search tree) est une structure de donnée utilsée pour localiser des neouds ayant des valeurs spécifiques dans un arbre enraciné (au sens de la théorie des graphe). Attention à ne pas confondre avec la notion de tree search qui correspond à la classe d'algorithme de parcours de graphe.

Annexes:

Pseudo-code des possibles implémentations

Algorithme minimax

function minimax(node, depth, maximizingPlayer) is
if depth = 0 or node is a terminal node then
    return the heuristic value of node
if maximizingPlayer then
    value := −∞
    for each child of node do
        value := max(value, minimax(child, depth − 1, FALSE))
    return value
else (* minimizing player *)
    value := +∞
    for each child of node do
        value := min(value, minimax(child, depth − 1, TRUE))
    return value

(* Initial call *)
minimax(origin, depth, TRUE)

Elagage αβ

function alphabeta(node, depth, α, β, maximizingPlayer) is
if depth = 0 or node is a terminal node then
    return the heuristic value of node
if maximizingPlayer then
    value := −∞
    for each child of node do
        value := max(value, alphabeta(child, depth − 1, α, β, FALSE))
        α := max(α, value)
        if α ≥ β then
            break (* β cut-off *)
    return value
else
    value := +∞
    for each child of node do
        value := min(value, alphabeta(child, depth − 1, α, β, TRUE))
        β := min(β, value)
        if α ≥ β then
            break (* α cut-off *)
return value

(* Initial call *)
alphabeta(origin, depth, −∞, +∞, TRUE)

Expectiminimax

function expectiminimax(node, depth)
if node is a terminal node or depth = 0
    return the heuristic value of node
if the adversary is to play at node
    // Return value of minimum-valued child node
    let value := +∞
    foreach child of node
        value := min(value, expectiminimax(child, depth-1))
else if we are to play at node
    // Return value of maximum-valued child node
    let value := -∞
    foreach child of node
        value := max(value, expectiminimax(child, depth-1))
else if random event at node
    // Return weighted average of all child nodes' values
    let value := 0
    foreach child of node
        value := value + (Probability[child] * expectiminimax(child, depth-1))
return value

(* Initial call *)
expectiminimax(origin, depth)

Sources

Page wikipedia pour l'algorithme Minimax
Page wikipedia pour l'algorithme d'élagage alpha-beta
Page wikipedia pour l'algorithme expectiminimax
Chapitres 3 à 5 du livre Artificial Intelligence, A modern approach, 3ème édtition. Sutart Russel & Peter Norwig, Pearson.
Thèse de J,A,M Nijssen, Monte-Carlo tree search for multiplayer games
Chapitre 5 du cours Adevrsarial search and game playing, Olivier schulte