Introduction

Les types de données au format Réel appartiennent à la famille EDT (Elementary data type, type de données élémentaires), qui contient des types de données simples et non dérivés (tableaux, structures, blocs fonction).

Rappel concernant le format Réel

Le format Réel (virgule flottante selon la norme ANSI/IEEE 754) utilise un codage de format 32 bits qui correspond aux nombres réels à virgule flottante à une décimale.

Les 32 bits qui représentent la valeur à virgule flottante sont organisés dans les trois champs distincts qui sont :

  • S, le bit de signe qui peut avoir l'une des valeurs suivantes :

    • 0, pour un nombre à virgule flottante positif

    • 1, pour un nombre à virgule flottante négatif

  • e, l'exposant codé dans un champ de 8 bits (entier au format binaire)

  • f, la partie correspondant à la virgule décimale dans un champ de 23 bits (entier au format binaire)

Représentation :

La valeur de la partie correspondant à la virgule décimale (Mantissa) est comprise entre [0, 1[, et calculée avec la formule ci-après.

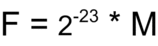
Types de nombres pouvant être représentés

Il s'agit des nombres suivants :

  • normalisés

  • non normalisés

  • de valeur infinie

  • avec les valeurs + 0 et - 0

Le tableau suivant indique les valeurs dans les différents champs suivant le type de nombre.

e

f

S

Type de nombre

]0, 255[

[0, 1[

0 ou 1

normalisé

0

[0, 1[

environ (1.4E-45)

non normalisé DEN

255

0

0

+ infini (INF)

255

0

1

- infini (-INF)

255

]0,1[ et bit 22 = 0

0 ou 1

SNAN

255

]0,1[ et bit 22 = 1

0 ou 1

QNAN

0

0

0

+0

0

0

1

-0
NOTE : La norme IEC 559 définit deux classes de NAN (Pas un nombre) : QNAN et SNAN.

  • QNAN : NAN dont le bit 22 correspond à 1

  • SNAN : NAN dont le bit 22 correspond à 0

Elles se comportent comme suit :

  • Les QNAN ne provoquent pas d'erreurs lorsqu'ils apparaissent dans les opérandes d'une fonction ou d'une expression.

  • Les SNAN provoquent une erreur lorsqu'ils apparaissent dans les opérandes d'une fonction ou d'une expression mathématique (voir %SW17 et %S18).

Le tableau ci-dessous présente la formule de calcul de la valeur du nombre à virgule flottante :

Nombre à virgule flottante

Valeur

Normalisé

Non normalisé (DEN)

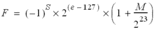NOTE : Un nombre réel compris entre -1,1754944e-38 et 1,754944e-38 est un nombre non normalisé DEN. Lorsqu'une opérande correspond à un DEN, le résultat n'est pas garanti. Les bits %SW17 et %S18 sont augmentés, sauf pour le Modicon M340. Les automates Modicon M340 peuvent utiliser des opérandes non normalisés, mais avec une perte de précision en raison du format. Le dépassement inférieur est signalé suivant l'opération uniquement lorsque le résultat est égal à 0 (dépassement inférieur total) ou lorsqu'il est non normalisé (dépassement inférieur graduel, avec perte de précision).

Type réel

Présentation :

Type

Echelle (bits)

Valeur par défaut

REAL

32

0.0

Plage de valeurs (parties grisées) :

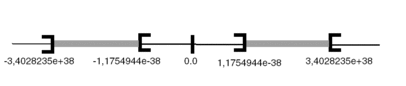
Lorsqu'un résultat est :

  • compris entre -1,1754944e-38 et 1,1754944e-38, il s'agit d'un DEN ;

  • inférieur à -3,4028234e+38, le symbole -INF (pour - infini) s'affiche ;

  • supérieur à +3,4028234e+38, le symbole INF (pour + infini) s'affiche ;

  • indéfini (racine carrée d'un nombre négatif), le symbole NAN s'affiche.

Exemple de valeur normalisée inexacte

7,986 est codé de la façon suivante par l'application :

S

E=129

M=8359248

0

1000001

11111111000110101010000

Avec la formule :

Le nombre 7,986 devrait correspondre à :

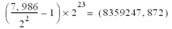
Le significatif étant exprimé sous forme d'entier, il peut être codé uniquement sous la forme 8359248 (arrondi à la limite la plus proche).

Aucun nombre ne peut être codé entre le chiffre significatif 8359247 et 8359248, ou entre le nombre réel 7,985999584197998046875 et 7,98600006103515625

Poids du bit le moins significatif (écart) en précision absolue :

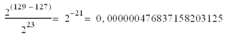
L'écart devient très important pour les valeurs élevées comme indiqué ci-dessous :

Valeur

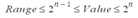M=8359248

100 000 000

Entre 226 et 227

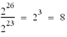2127

2127

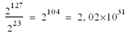NOTE : L'écart correspond au poids du bit le moins significatif.

Pour obtenir la résolution attendue, il est nécessaire de définir la plage maximale du calcul conformément à la formule suivante :

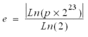
p correspond à la précision et e à l'exposant (e = E-127)

Par exemple, si la précision doit être égale à 0,001, la partie correspondant à la virgule décimale sera :

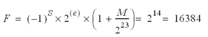
avec :

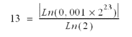
Au-delà de la limite F, la précision est perdue.

Cas classique : compteurs

Il convient de faire preuve de discernement dans l'utilisation des nombres à virgule flottante, en particulier lorsqu'il est nécessaire d'y ajouter une faible valeur.

Lors de petits incréments, le compteur ne fonctionne pas correctement et donne des résultats erronés sans augmentation lorsque l'incrément est inférieur au bit le moins significatif du compteur.

Pour obtenir des valeurs correctes, il est recommandé de s'appuyer sur un entier double (UDINT) et de multiplier le résultat par un incrément.

Exemple :

  • Incrémentez une valeur de 0,001 de 33000 à 1000000.

  • Comptez de 33000000 à 1000000000 (valeur multipliée par 1000) avec un agrément de 1.

  • Obtenez le résultat en multipliant la valeur par 0,001.

La précision minimale F par plage sera la suivante :

De...à...

F (minimum)

3300 à 65536

0,004

65536 à 131072

0,008

...

...

524288 à 1000000

0,063

Ce compteur peut aller jusqu'à 4294967295 x 0,001 = 4294967,5 avec une précision minimale de 0,5

NOTE : Ici, la valeur réelle correspond à la valeur binaire codée. Elle peut être différente de l'affichage sur un écran d'exploitation en raison de l'arrondi (4,294968e+006)