Introduction
The data types in Real format belong to the EDT (Elementary data type) family, which includes single rather than derived data types (tables, structures, function blocks).
Reminder Concerning Real Format
The Real format (floating point in ANSI/IEEE 754 standard) is coded in 32 bit format which corresponds to the single decimal point floating numbers.
The 32 bits representing the floating point value are organized in three distinct fields. These are:
S, the sign bit which can have the value:
0, for a positive floating point number
1, for a negative floating point number
e, the exponential coded in an 8 bit field (integer in binary format)
f, the fixed-point part coded in a 23 bit field (integer in binary format)
Representation:

The value of the fixed-point part (Mantissa) is between [0, 1[, and is calculated using the following formula.
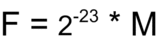
Number Types that Can Be Represented
These are the numbers which are:
normalized
denormalized
of infinite values
with values +0 and -0
This table gives the values in the different fields according to number type.
e |
f |
S |
Number type |
|---|---|---|---|
]0, 255[ |
[0, 1[ |
0 or 1 |
normalized |
0 |
[0, 1[ |
near (1.4E-45) |
denormalized |
255 |
0 |
0 |
+ infinity (INF) |
255 |
0 |
1 |
- infinity (-INF) |
255 |
]0,1[ and bit 22 = 0 |
0 or 1 |
|
255 |
]0,1[ and bit 22 = 1 |
0 or 1 |
|
0 |
0 |
0 |
+0 |
0 |
0 |
1 |
-0 |
NAN (not a number): QNAN and SNAN.QNAN: is aNANwhose bit 22 is set to 1SNAN: is aNANwhose bit 22 is set to 0
This table gives the calculation formula of the value of the floating-point number:
Floating-point number |
Value |
|---|---|
Normalized |
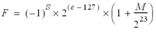 |
Denormalized ( |
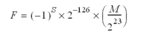 |
DEN. When an operand
is a DEN, the result is not guaranteed. The bits %SW17 and %S18 are raised except
for the Modicon M340. The Modicon M340 PLCs are able to use the denormalized
operands but, due to the format, with a loss of precision. Underflow
is signaled depending on the operation only when the result is 0 (total
underflow) or when the result is a denormalized (gradual underflow,
with loss of precision).The Real Type
Presentation:
Type |
Scale (bits) |
Default value |
|---|---|---|
REAL |
32 |
0.0 |
Range of values (grayed out parts):
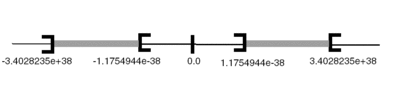
When a calculation result is:
between -1.1754944e-38 and 1.1754944e-38, it is a
DENless than -3.4028234e+38, the symbol
-INF(for -infinite) is displayedgreater than +3.4028234e+38, the symbol
INF(for +infinite) is displayedundefined (square root of a negative number), the symbol
NANis displayed
Examples of inaccuracy on normalized value
7.986 will be coded by the application as:
S |
E=129 |
M=8359248 |
|---|---|---|
0 |
1000001 |
11111111000110101010000 |
Using the formula:
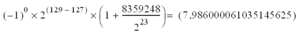
The number 7.986 should have a significant of:
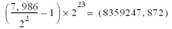
As the significant is expressed as an integer, it can only be coded as 8359248 (rounded to the nearest limit).
No number can be coded between the significant 8359247 and 8359248, or between the real number 7.985999584197998046875 and 7.98600006103515625
The weight of the less significant bit (gap) is, in absolute precision:
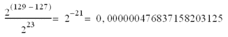
The gap becomes very important for big values as shown below:
Value |
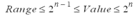 |
M=8359248 |
|---|---|---|
100 000 000 |
Between 226 and 227 |
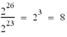 |
2127 |
2127 |
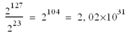 |
In order to get an expected resolution, it is necessary to define the maximum range for the calculation according the following formula:
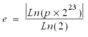
p being the accuracy and e the exponent (e = E-127)
For instance, if the accuracy needs to be = 0.001, the fixed-point part will be:
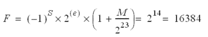
with:
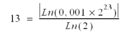
Beyond of this limit F, the accuracy will be lost.
Typical case: Counters
Floating must be used carefully, especially when it needs to add a small number to itself.
In case of small increments, the counter won't count properly, giving wrong results and stopping to rise when the increment will be lower than the less significant bit of the counter.
To get correct values, it is recommended to count on an double
integer (UDINT) and multiply the result by the increment.
Example:
Increment a value by 0.001 from 33000 to 1000000,
Count from 33000000 to 1000000000 (value times 1000) with 1 as increment,
Get the result multiplying the value by 0.001.
The accuracy F minimum per range will be:
From...to... |
F (minimum) |
|---|---|
3300...65536 |
0.004 |
65536...131072 |
0.008 |
... |
... |
524288...1000000 |
0.063 |
This counter can raise up to 4294967295 x 0.001 = 4294967.5 with a minimum accuracy of 0.5


