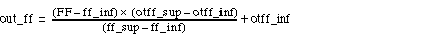Mixed/parallel structure (
mix_par)
Structure selection takes place via the mix_par parameter:
|
If
|
Then
|
|
mix_par = 0
|
there is a mixed structure, i.e. the proportional component is set up in the connection to the integral and differential component. The gain K set up for the components (see Structure diagram) corresponds to kp. |
|
mix_par = 1
|
the structure is parallel, i.e. the proportional coefficient is set up parallel to the integral and differential coefficient. In this case, the gain kp does not related to the integral and differential component. In this case, gain K corresponds to the relationship between the output zone and the range.
|
Absolute algorithms (
ti = 0)
Absolute algorithms are used when no integral component is set up (ti = 0). In this case the output OUT is calculated first, and then the output alteration is deducted.
Incremental algorithms (
ti > 0)
Incremental algorithms are used when an integral component is present (i.e. when ti > 0). The special feature of this algorithm is that the output alteration OUTD is calculated first and then an absolute value output is determined according to the following formula:
This algorithm form makes it possible to switch a
SERVO function block to the controller and thus to attain astatic control.
The incremental form also offers the following possibilities:
|
Possibility
|
Explanation
|
|
External block integral component
(with en_rcpy = 1)
|
If the real component deviates from the value calculated by the controller (with an open servoloop), the real value should be used as the basis for the calculation. If this value is available, it should be assigned to the RCPY input and the parameter en_rcpy must be switched to 1. In calculations done by the function block, the equation
OUT(new) = OUT (old) + OUTD
to
OUT (new) = RCPY+ OUTD
This is particularly beneficial for cascades or cascade-like controls.
Note: In this case the OUT output is not limited.
|
|
Expanded anti-windup measure
|
The incremental form of the PID controller offers as standard an anti-windup measure taken into account in the algorithm. This type is the basis when aw_type = 0. In this case the output can be saturated and suddenly leave its threshold, even if the sign of the deviation does not change (e.g. if it is affected by a brief disturbance during measuring). It is possible to use a second anti-windup measure (aw_type = 1) which prevents the output from exceeding its threshold as long as the deviation does not alter the sign.
|
Weight of the setpoint in the proportional component (reducing the overrun)
If an integral component is present (
ti > 0), the
ovs_att parameter makes the weight of the proportional component possible the calculation of the proportional component is based on the weighted deviation (
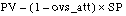
).
This could have an influence in the case of an overrun, as can occur with setpoint modifications. The aim is to retain a control-intensive proportional component and therefore a dynamic response to disturbances without an overrun occurring during control.
The parameter ovs_att can fluctuate continually between:
|
Value
|
Meaning
|
|
0
|
to the proportional component (classic case) assigned to the deviation (system deviation)
|
|
1
|
for the proportional component (with sensitive processes or processes with an integral effect) assigned to the measurement (controlled variable).
|
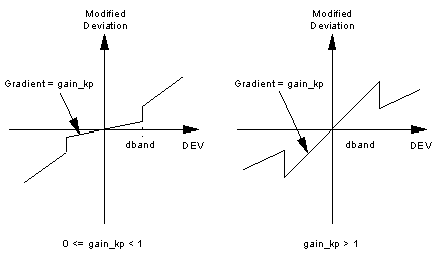
Dead zone on deviation (
dband)
When the operating point is reached the dead zone can limit smaller values to the actuator’s value. as long as the deviation lies below dband, the calculation of the function block is based on the value zero.
The extended parameter gain_kp can be used to modify the deviation inside the dead zone. This is better than deleting it. The modified deviation (multiplied by gain_kp) is used to calculate the proportional and integral components.
Representation of the alteration of the deviation
Transfer gain with the differential component
The PIDFF function block contains a filter of the first order for the differential component. The filter gain kd can be configured so that processes where the differential component must be very strongly filtered can be processed as well as processes where the filtering of the differential component can be removed because the signal is "pure" enough.
Feed forward component for disturbance compensation (
FF input)
With classic PID control, the controller reacts to output modifications of the control process (closed servoloop). In the case of a disturbance, the controller only reacts if the process value deviates from the setpoint value. The feed-forward-function means that a measurable disturbance can be compensated for as soon as it arises. This function, conceived as an open servoloop, removes the effects of the disturbance. in this case the term disturbance size update (Feed Forward) is used.
The component of the feed forward input is updated directly/inversely to the manipulated variable of the controller after the control direction has been included.
The calculation proceeds according to the following formula:
NOTE: If ff_sup = ff_inf, the calculation of the Feed-Forward component is ignored.
The block contains the following properties:
-
The outbias parameter makes precision at the operating point possible if the process contains no integral component (ti = 0).
-
In automatic mode, the OUT output is limited to the range between out_min and out_max, and to the range between out_inf and out_sup in manual mode. If a value calculated by the function block (or a written value entered by the user in manual mode) exceeds one of these limits, the value of OUT is capped. The incremental output OUT_D, however, does not take this capping into consideration. This enables the PIDFF function block to control a SERVO function block without having to revert the position of the actuator (continuous control).
-
The output speed increase is limited by the parameter outrate.
-
The possibility of selecting between direct/inverse action (parameter rev_dir) allows for the adjustment of the control direction of the link actuator/ process.
-
The differential component can affect both the process value (pv_dev = 0), and the deviation (pv_dev = 1)
-
pv_inf and pv_sup correspond to the upper and lower thresholds of the setpoint value.
-
The function block can also have an effect in pure integral mode (with kp = 0).

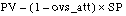 ).
).