Calcul de l'accélération - sur les mesures filtrées

Filtrage numérique filtre numérique d'ordre 1

Le concept est d'obtenir une liste de signal filtré \(LF\) à partir d'une liste de non filtrée \(L\) et d'une liste de temps \(T\).

La relation est de la forme \(\tau\frac{dLF(t)}{dt}+LF(t)=L(t)\).

Méthode : Pour une grandeur \(u(t)\) qui pourra être \(e(t)\) ou \(s(t)\), il s'agira d'exploiter la relation qui exprime la fonction de dérivation, sous la forme de différence finie : \(\frac{{d\left( {u\left( t \right)} \right)}}{{dt}} \approx \frac{{\Delta U}}{{\Delta t}}\) s'écrira donc \(\frac{{U\left( {{t_n}} \right) - U\left( {{t_{n - 1}}} \right)}}{{{t_n} - {t_{n - 1}}}}\) avec \({t_n} - {t_{n - 1}}\) la période d'échantillonnage.

Question

Q4/ Écrire la relation de récurrence qui permet d'obtenir la liste \(LF\).

Indice

On pose \(dt=T_l[i+1]-T_l[i]\)

\(\tau\frac{LF[i+1]-LF[i]}{dt}+LF[i]=L[i]\).

On pose \(h=dt/tau\)

On a alors \(LF[i+1]=hL[i]+(1-h)LF[i]\)

Question

Q5/ Écrire la fonction \(filtre(L,tau,T)\) qui prend en argument deux listes de même taille \(L\) et \(T\) ainsi qu'un réel \(tau\) et qui renvoie la liste \(L\) filtrée. Tracer la courbe. La valeur de \(\tau\) sera prise égale au pas d'échantillonnage (\(0.02~ s\)).

Solution

1
def filtre(L_l,tau,T_l):
2
    n=len(T_l)
3
    S=[0]*n
4
    for i in range(0,n-1):
5
        dt=T_l[i+1]-T_l[i]
6
        h=dt/tau
7
        S[i+1]=(h*L_l[i]+(1-h)*S[i])
8
    return(S)
9
10
YPPF=filtre(YPP,0.02,T) #Calcul acceleration filtrée filtre d'ordre1 
11
12
####################################################################
13
#tracé accélération + acceleration filtrée par filtre ordre 1 
14
#####################################################################
15
plt.figure()
16
plt.plot(T,YPP,label="accélération")
17
plt.plot(T,YPPF,label="filtre ordre 1")
18
plt.legend()
19
plt.ylabel('accélération')
20
plt.xlabel("temps en s")
21
plt.show()
Réalisation d'un filtre par moyenne glissante
La moyenne glissante est une moyenne qui au lieu d'être calculée sur l'ensemble des \(n\) valeurs d'un échantillonnage, est calculée tour à tour sur chaque sous-ensemble de \(N\) valeurs consécutives (\(N≤n\) ) ; le sous-ensemble utilisé pour calculer chaque moyenne « glisse » sur l'ensemble des données. On appelle \(N\), l'ordre de la moyenne glissante.
Une formule permettant de calculer une moyenne mobile est : \(\overline {{x_n}} = \frac{1}{N}\mathop \sum \limits_{k = 0}^{N - 1} {x_{n - k}}\;{\rm{ou}}\;\overline {{x_n}} = {\bar x_{n - 1}} + \frac{{{x_n} - {x_{n - N}}}}{N}\;\)
Question
Q6/ Écrire une fonction \(filtre\_mg(L,N)\) qui prend en argument une liste \( L\) ainsi que l'ordre de la moyenne glissante \(N\) et qui retourne la liste \(L\) filtrée. Tester sur la courbe d'accélération et afficher le résultat obtenu pour différentes valeurs de \(N\).
Solution
1
def filtre_mg(l,N):
2
    res = list(l) # recopier la liste sans que la modif affecte les deux !!!
3
    for i in range(len(res)-N):
4
        somme=0
5
        for j in range (N):
6
           somme=somme+res[i+j]
7
        res[i]=somme/N
8
    return(res)
9
10
11
YPPF_MG=filtre_mg(YPPF,8) #Calcul acceleration filtrée moyenne glissante
12
13
Question
Q7/ Tracer le résultat du filtre d'ordre 1 et de la moyenne glissante sur le même graphique.
Indice
Solution
1
####################################################################
2
#tracé accélération + acceleration filtrée par filtre ordre 1 et moyenne glissante
3
#####################################################################
4
plt.figure()
5
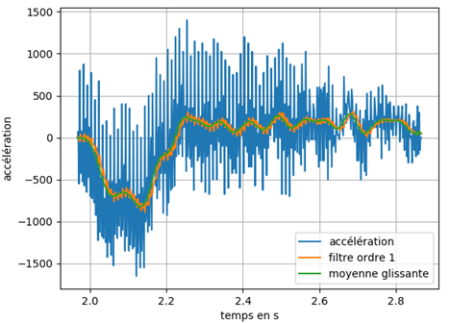
plt.plot(T,YPP,label="accélération")
6
plt.plot(T,YPPF,label="filtre ordre 1")
7
plt.plot(T,YPPF_MG,label="moyenne glissante")
8
plt.legend()
9
plt.ylabel('accélération')
10
plt.xlabel("temps en s")
11
plt.show()