Restaurant sous-marin
Le Rangali Island Restaurant est un restaurant dans les Maldives proposant une salle sous-marine.
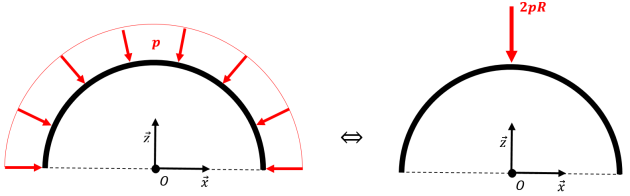
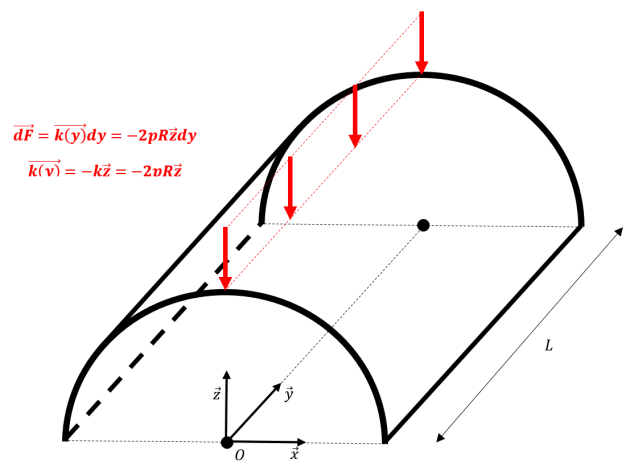
Dans le but de dimensionner la structure supportant la baie vitrée, nous souhaitons déterminer le torseur de l'action de l'eau sur celles-ci. On suppose que les baies vitrées ont une structure cylindrique de rayon constant \(R\) et on propose le modèle suivant, pour une tranche d'épaisseur \(dy\) :
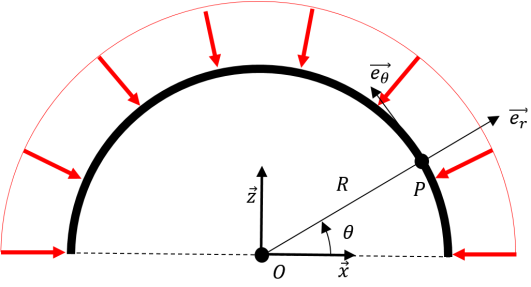
Nous négligerons la variation de pression entre le haut et le bas des baies vitrées et supposerons qu'elle est constante \(p={{p}_{0}}+\rho gh\) où \(\rho \) est la masse volumique de l'eau, \(g\) l'accélération de la pesanteur, \(h\) la profondeur et \({{p}_{0}}\) la pression atmosphérique.
\(\rho =1000~kg.{{m}^{-3}}~~~~~;~~~~~g=9,81~m.{{s}^{-2}}~~~~~;~~~~~h=10m~~~~~;~~~~~{{p}_{0}}=101325~Pa\)
\(R=2,5~m~~~~~;~~~~~L=15~m\)
Appelons \(L\) la longueur de la structure.
Question
Q1. Déterminer le torseur \(\left\{ dT \right\}\) de l'action de l'eau sur la structure en \(O\) dans la tranche de longueur \(dy\).
Solution
Q1. Déterminer le torseur \(\left\{ dT \right\}\) de l'action de l'eau sur la structure en \(O\) dans la tranche de longueur \(dy\)
Résultante | Moment |
|---|---|
\(\overrightarrow{dR}=-pdydl\overrightarrow{{{e}_{r}}}=-pRdy\overrightarrow{{{e}_{r}}}d\theta \) \(dl=Rd\theta \) \(\vec{R}=\underset{\Gamma }{\mathop \int }\,\overrightarrow{dR}=\underset{0}{\overset{\pi }{\mathop \int }}\,-pRdy\overrightarrow{{{e}_{r}}}d\theta =-pRdy\underset{0}{\overset{\pi }{\mathop \int }}\,\overrightarrow{{{e}_{r}}}d\theta \) \(\overrightarrow{{{e}_{r}}}=\cos \theta \vec{x}+\sin \theta \vec{z}\) \(\vec{R}=-pRdy\left[ \underset{0}{\overset{\pi }{\mathop \int }}\,\cos \theta d\theta \vec{x}+\underset{0}{\overset{\pi }{\mathop \int }}\,\sin \theta d\theta \vec{z} \right]\) \(\vec{R}=-pRdy\left[ \left[ \sin \theta \right]_{0}^{\pi }\vec{x}-\left[ \cos \theta \right]_{0}^{\pi }\vec{z} \right]\) \(\vec{R}=-2pRdy\vec{z}\) | \(\overrightarrow{d{{M}_{0}}}=\overrightarrow{OP}\wedge \overrightarrow{dR}=R\overrightarrow{{{e}_{r}}}\wedge -pRdy\overrightarrow{{{e}_{r}}}d\theta \) \(\overrightarrow{d{{M}_{0}}}=\vec{0}\) \(\overrightarrow{{{M}_{0}}}=\underset{\Gamma }{\mathop \int }\,\overrightarrow{d{{M}_{0}}}=\vec{0}\) |
\(\left\{ dT \right\}={{\left\{ \begin{matrix} -2pRdy\vec{z} \\ {\vec{0}} \\ \end{matrix} \right\}}_{O}}={{\left\{ \begin{matrix} 0 & 0 \\ 0 & 0 \\ -2pRdy & 0 \\ \end{matrix} \right\}}_{O}}\)
Question
Q2. En déduire un modèle simple de l'action de l'eau sur la tranche étudiée.
Solution
Q2. En déduire un modèle simple de l'action de l'eau sur la tranche étudiée
On peut remplacer l'action répartie sur la tranche du cylindre par un « effort ponctuel en plan » ou un effort linéique sur la droite passant par \(O\) et parallèle à \(\vec{z}~\): \(\left( O,\vec{z} \right)\)
Question
Q3. Montrer en particulier que la valeur de cet effort (par unité de longueur) est liée à la « ligne » de longueur \({{L}_{p}}=2R\) correspondant à la projection de la baie. Intéressons-nous maintenant à la baie vitrée sur toute sa longueur. On propose le modèle suivant :
Solution
Q3. Montrer en particulier que la valeur de cet effort (par unité de longueur) est liée à la « ligne » de longueur \({{L}_{p}}=2R\) correspondant à la projection de la baie
\(\vec{R}=-2pR\vec{z}=-p{{L}_{p}}\vec{z}\)
Question
Q4. Compte tenu de l'étude précédente, proposer un modèle simple sous forme d'action linéique pour représenter l'action de l'eau sur la structure étudiée.
Solution
Q4. Compte tenu de l'étude précédente, proposer un modèle simple sous forme d'action linéique pour représenter l'action de l'eau sur la structure étudiée
Question
Q5. En déduire un modèle de l'action de l'eau sous forme d'une action ponctuelle \(\vec{R}\) en un point \(A\) dont la position sera précisée.
Solution
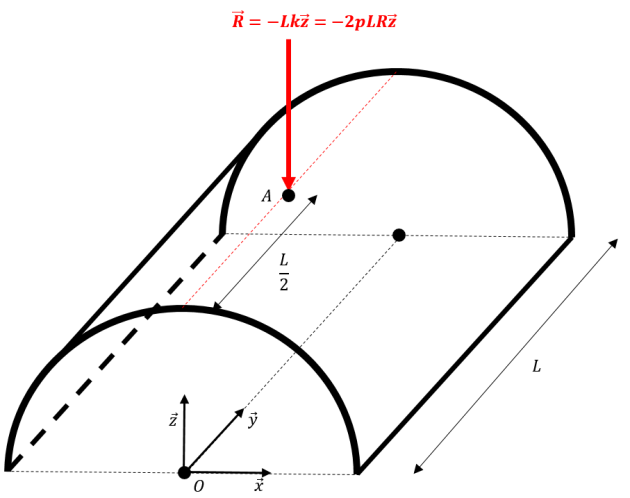
Q5. En déduire un modèle de l'action de l'eau sous forme d'une action ponctuelle \(\vec{R}\) en un point \(A\) dont la position sera précisée
Question
Q6. En déduire le torseur \(\left\{ T \right\}\) de l'action de l'eau sur la structure en \(O\).
Solution
Q6. En déduire le torseur \(\left\{ T \right\}\) de l'action de l'eau sur la structure en \(O\)
\(\left\{ T \right\}={{\left\{ \begin{matrix} -2pLR\vec{z} \\ {\vec{0}} \\ \end{matrix} \right\}}_{A}}={{\left\{ \begin{matrix} -2pLR\vec{z} \\ -p{{L}^{2}}R\vec{x} \\ \end{matrix} \right\}}_{O}}\)
Méthode intégrale inutile ici :
Résultante | Moment |
|---|---|
\(\overrightarrow{dR}=-k\vec{z}dy\) \(\vec{R}=\underset{\Gamma }{\mathop \int }\,\overrightarrow{dR}=\underset{0}{\overset{L}{\mathop \int }}\,-k\vec{z}dy=-kL\vec{z}=-2RLp\vec{z}\) | \(\overrightarrow{d{{M}_{0}}}=\overrightarrow{OP}\wedge \overrightarrow{dR}=y\vec{y}\wedge -k\vec{z}dy=-yk\vec{x}dy\) \(\overrightarrow{{{M}_{0}}}=\underset{\Gamma }{\mathop \int }\,\overrightarrow{d{{M}_{0}}}=\underset{0}{\overset{L}{\mathop \int }}\,-yk\vec{x}dy=-k\underset{0}{\overset{L}{\mathop \int }}\,ydy\vec{x}\) \(\overrightarrow{{{M}_{0}}}=-k\frac{{{L}^{2}}}{2}\vec{x}=-p{{L}^{2}}R\vec{x}\) |
Question
Q7. Montrer que la valeur de cette résultante est liée à la surface projetée \({{S}_{p}}=2RL\).
Solution
Q7. Montrer que la valeur de cette résultante est liée à la surface projetée \({{S}_{p}}=2RL\)
\(\vec{R}=-2RLp\vec{z}=-p{{S}_{p}}\vec{z}\)
Question
Q8. Déterminer les valeurs numériques de la résultante et du moment de cette action en \(O\).
Solution
Q8. Déterminer la valeur numérique de la résultante de cette action
\(R=2RLp=2RL\left( {{p}_{0}}+\rho gh \right)=2*2,5*15*\left( 101325+1000*9,81*10 \right)\)
\(R=2RLp=2RL\left( {{p}_{0}}+\rho gh \right)=75*199~425=14~956~900~N\)
Remarque : Imaginons que la salle complète soit plongée dans l'eau et soumise à une pression constante (pas d'effets de la gravité). Dans ce cas, il n'existe pas de poussée d'Archimède et le solide soumis à cette pression est en équilibre, c'est-à-dire que résultante et moment de l'action de pression sur le solide sont nuls.
Appelons \(S\) la surface du demi-cylindre et \({S}'\) la surface plane du sol soumise à la pression fictive de l'eau.
Question
Q9. Donner la relation liant \(\underset{S}{\mathop \int }\,-p\vec{n}dS\) et \(\underset{{{S}'}}{\mathop \int }\,-p\vec{n}dS\).
Solution
Q9. Donner la relation liant \(\underset{S}{\mathop \int }\,-p\vec{n}dS\) et \(\underset{{{S}'}}{\mathop \int }\,-p\vec{n}dS\)
\(\vec{R}=\underset{S}{\mathop \int }\,-p\vec{n}dS+\underset{{{S}'}}{\mathop \int }\,-p\vec{n}dS=0\)
Question
Q10. En déduire l'expression de la résultante de l'action de pression sur le demi-cylindre \(S\) en fonction de \(p\), \(R\) et \(L\).
Solution
Q10. En déduire l'expression de la résultante de l'action de pression sur le demi-cylindre \(S\) en fonction de \(p\), \(R\) et \(L\)
\(\underset{{{S}'}}{\mathop \int }\,-p\vec{n}dS=-\underset{S}{\mathop \int }\,-p\vec{n}dS=-\underset{S}{\mathop \int }\,-p\left( -\vec{z} \right)dS=-\underset{S}{\mathop \int }\,p\vec{z}dS=-p\underset{S}{\mathop \int }\,dS\vec{z}=-2RpL\vec{z}\)
On remarquera que ce résultat est vrai pour toute surface qui peut être fermée par un plan, quelle que soit sa géométrie, et on pourra étendre ce résultat à une ligne fermée par un segment.